
- •Теория поля
- •Составители: елисеев Игорь Спартакович
- •Содержание
- •1 Скалярное поле. Производная по направлению и градиент
- •2 Векторное поле. Векторные линии
- •3 Поток векторного поля
- •4 Формула остроградского. Дивергенция векторного поля
- •5 Линейный интеграл и циркуляция векторного поля
- •6 Ротор векторного поля. Формула стокса
- •7 Потенциальное векторное поле. Вычисление линейного интеграла в потенциальном поле
- •8. Варианты заданий
8. Варианты заданий
Первые три задачи каждого варианта необходимо решить при следующих условиях:
Найти работу векторного поля
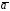 вдоль заданной кривой
вдоль заданной кривой .
.
Пользуясь формулой Остроградского-Гаусса, вычислить поток вектора
 через ориентированную поверхность
через ориентированную поверхность
Пользуясь формулой Стокса, найти циркуляцию вектора
 по контуру
по контуру в положительном направлении относительно
вектора
в положительном направлении относительно
вектора .
.
Вариант № 1




 ;
;
 - внешняя сторона боковой поверхности
конуса
- внешняя сторона боковой поверхности
конуса
 ;
;
 .
.Показать, что поле вектора
 потенциально, найти его потенциал.
потенциально, найти его потенциал.
Вариант № 2


 от
от до
до
 ;
;
 - внешняя сторона части параболоида
- внешняя сторона части параболоида отсеченного плоскостью
отсеченного плоскостью
 ;
;

Вычислить ротор векторного поля
 где
где -
постоянный вектор,
-
постоянный вектор,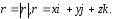
Вариант № 3
 ;
;


 -
внешняя сторона полусферы
-
внешняя сторона полусферы

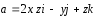 ;
;
 - контур, образованный пересечением
плоскости
- контур, образованный пересечением
плоскости с координатными плоскостями;
с координатными плоскостями;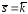 .
.Найти производную скалярного поля
 в точке
в точке в направлении градиента поля
в направлении градиента поля в точке
в точке .
.
Вариант № 4


 от
точки
от
точки
 до
до
 ;
;
 -
внешняя сторона части поверхности
параболоида
-
внешняя сторона части поверхности
параболоида
 ;
;
 - контур треугольника
- контур треугольника
Вычислить дивергенцию векторного поля
 где
где и
и - постоянные векторы, а
- постоянные векторы, а
Вариант № 5
 ;
;
 отрезок
прямой от точки
отрезок
прямой от точки до точки
до точки
 ;
;
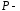 внешняя сторона поверхности цилиндра
внешняя сторона поверхности цилиндра ,
ограниченного плоскостями
,
ограниченного плоскостями и
и
 ;
;
 -
линия пересечения цилиндра
-
линия пересечения цилиндра с плоскостью
с плоскостью
Вычислить дивергенцию поля
 где
где
Вариант № 6


 .
. ;
;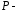 внешняя
сторона боковой поверхности пирамиды,
ограниченной плоскостями
внешняя
сторона боковой поверхности пирамиды,
ограниченной плоскостями

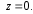
 ;
;
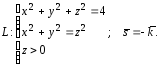
Найти ротор векторного поля

Вариант № 7
 ;
;
 от точки
от точки до точки
до точки

 внешняя
сторона части сферы
внешняя
сторона части сферы
 отсеченной плоскостью
отсеченной плоскостью
 ;
;

Вычислить дивергенцию векторного поля
 где
где
Вариант № 8

 ;
;
 контур
треугольника
контур
треугольника
 ;
;
 внешняя сторона боковой поверхности
пирамиды, ограниченной плоскостями
внешняя сторона боковой поверхности
пирамиды, ограниченной плоскостями
 ;
; 
Проверить, является ли соленоидальным векторное поле

Вариант № 9

 ;
;
 контур
контур
 ;
;
 внешняя сторона полусферы
внешняя сторона полусферы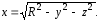
 ;
; 
Является ли поле, образованное вектором
 потенциальным?
потенциальным?
Вариант № 10

 ;
от
;
от
 до
до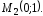
2.
 ;
; внешняя сторона боковой поверхности
цилиндра
внешняя сторона боковой поверхности
цилиндра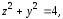 ограниченного плоскостями
ограниченного плоскостями
3.
 ;
;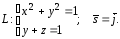
4.
Доказать, что поле вектора
 потенциально и найти его потенциал.
потенциально и найти его потенциал.
Вариант № 11

1. ;
; первая
арка кривой
первая
арка кривой
2.
 ;
; внешняя сторона цилиндрической
поверхности
внешняя сторона цилиндрической
поверхности ограниченной плоскостями
ограниченной плоскостями
3.
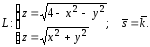
4.
Найти дивергенцию поля
 где
где
Вариант № 12

1.

 от
от до
до .
.
2.
 ;
; внешняя сторона поверхности конуса
внешняя сторона поверхности конуса
3.


4.
Найти производную функции
 в точке (2;1) в направлении, идущем от этой
точки к началу координат.
в точке (2;1) в направлении, идущем от этой
точки к началу координат.
Вариант № 13
 ;
;
 от точки
от точки до точки
до точки

 ;
;
 внешняя сторона поверхности параболоида
внешняя сторона поверхности параболоида ограниченного плоскостью
ограниченного плоскостью


Вычислить дивергенцию векторного поля
 в точке (1;1/2;-1).
в точке (1;1/2;-1).
Вариант № 14



 от
от
 до
до

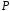 -внешняя
сторона однополостного гиперболоида
-внешняя
сторона однополостного гиперболоида
 ограниченного плоскостями
ограниченного плоскостями .
. ;
;
 пересечение
параболоида
пересечение
параболоида с координатными плоскостями
с координатными плоскостями

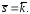
Вычислить ротор векторного поля
 где
где -
постоянный вектор, а
-
постоянный вектор, а
Вариант № 15
 ;
;
 от точки
от точки до точки
до точки
 ;
;
 -внешняя
сторона поверхности конуса,
-внешняя
сторона поверхности конуса, ограниченной плоскостями
ограниченной плоскостями
 ;
;


 .
.Проверить, является ли векторное поле

 потенциальным,
и если оно потенциально, то вычислить
его потенциал.
потенциальным,
и если оно потенциально, то вычислить
его потенциал.
Вариант № 16

 ;
;
 отрезок
отрезок от
от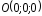 до
до
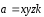 ;
;
 внешняя
сторона полусферы
внешняя
сторона полусферы
 ;
;
 .
.Вычислить дивергенцию поля
 где
где -
постоянный вектор.
-
постоянный вектор.
Вариант № 17

 ;
; ломаная
ломаная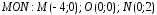 в направлении от
в направлении от к
к .
. ;
;
 внешняя сторона поверхности конуса
внешняя сторона поверхности конуса ограниченного сферой
ограниченного сферой
 ;
;

Вычислить дивергенцию векторного поля
 в точке (1;2;3).
в точке (1;2;3).
Вариант № 18

 ;
;
 отрезок
отрезок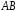 в направлении от точки
в направлении от точки к точке
к точке
 ;
;
 внешняя сторона цилиндра
внешняя сторона цилиндра
 ;
;

Вычислить ротор вектора
 где
где
Вариант № 19

 ;
;
 ломанная
ломанная

 .
. ;
;
 внешняя
сторона части поверхности параболоида
внешняя
сторона части поверхности параболоида
 ;
;
 .
.Найти производную функции
 в точке
в точке в направлении, идущем от этой точки к
точке
в направлении, идущем от этой точки к
точке
Вариант № 20

 ;
;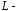 дуга
дуга одного витка винтовой линии
одного витка винтовой линии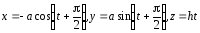 в направлении возрастания параметра.
в направлении возрастания параметра. ;
; внешняя сторона полусферы
внешняя сторона полусферы
3.
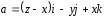 ;
; .
.
Найти потенциал векторного поля
 если оно потенциально.
если оно потенциально.
Вариант № 21

 ;
;
 от точки
от точки
 до точки
до точки .
.
 ;
;
 боковая поверхность пирамиды с вершиной
в точке
боковая поверхность пирамиды с вершиной
в точке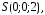 основанием которой служит треугольник
основанием которой служит треугольник
 ;
;

Векторное поле образовано вектором
 .
Доказать, что оно потенциально и найти
его потенциал;
.
Доказать, что оно потенциально и найти
его потенциал;
Вариант № 22

 ;
;
 прямая
прямая от
от к
к .
.
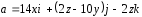 ;
;
 внешняя сторона части поверхности
параболоида
внешняя сторона части поверхности
параболоида отсеченной плоскостью
отсеченной плоскостью
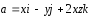 ;
;
 пересечение
плоскости
пересечение
плоскости с координатными плоскостями;
с координатными плоскостями;
Показать, что поле
 потенциально и найти его потенциал.
потенциально и найти его потенциал.
Вариант № 23

 ;
;
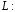
 от точки
от точки до точки
до точки
 ;
;
 внутренняя
сторона цилиндрической поверхности
внутренняя
сторона цилиндрической поверхности ограниченной плоскостями:
ограниченной плоскостями:
 ;
;

Показать, что векторное поле
 является потенциальным, и его потенциал
является потенциальным, и его потенциал является гармонической функцией,
удовлетворяющий уравнению Лапласа
является гармонической функцией,
удовлетворяющий уравнению Лапласа
Вариант № 24
1.
 ;
; от
от до
до .
.
2.
 ;
;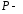 внутренняя
сторона поверхности параболоида
внутренняя
сторона поверхности параболоида ограниченного плоскостью
ограниченного плоскостью
3.
 ;
; контур треугольника
контур треугольника с вершинами
с вершинами и
и
4. Найти дивергенцию от градиента функции
 в
точке
в
точке

Вариант № 25


 контур
контур

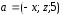 ;
; верхняя
сторона лежащей в первом октанте части
плоскости
верхняя
сторона лежащей в первом октанте части
плоскости
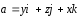 ;
;
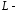 контур,
лежащий в первом октанте и образованный
пересечением поверхности
контур,
лежащий в первом октанте и образованный
пересечением поверхности с плоскостями
с плоскостями

Найти точки, в которых градиент функции
 равен
равен
Вариант № 26

 ;
;
 контур
контур .
. ;
;
 нижняя
поверхность части параболоида
нижняя
поверхность части параболоида отсеченной плоскостью
отсеченной плоскостью
 ;
;
 линия пересечения цилиндра
линия пересечения цилиндра с плоскостью
с плоскостью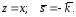
Доказать, что вектор
 ортогонален
ортогонален где
где а
а .
.
Вариант № 27

 ;
;

 от точки
от точки до точки
до точки
 ;
;
 верхняя
сторона поверхности сферы
верхняя
сторона поверхности сферы лежащей в 1-м октанте.
лежащей в 1-м октанте. ;
;
 часть
линии пересечения сферы
часть
линии пересечения сферы с плоскостями
с плоскостями лежащая в первом октанте;
лежащая в первом октанте;
Вычислить дивергенцию векторного поля
 где
где постоянный
вектор.
постоянный
вектор.
Вариант № 28


 ;
;
 поверхность
куба
поверхность
куба
 в направлении внешней нормали.
в направлении внешней нормали.
 ;
;

Найти величину и направление градиента поля
 в точке
в точке
Вариант № 29

 .
. ;
;
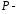 поверхность тела
поверхность тела
 ,
в направлении внешней нормали.
,
в направлении внешней нормали. ;
;


Найти дивергенцию поля
 в точке
в точке
Вариант № 30


 .
. ;
;
 поверхность
тела
поверхность
тела в направлении внешней нормали.
в направлении внешней нормали. ;
;
 контур, вырезаемый в первом октанте из
параболоида
контур, вырезаемый в первом октанте из
параболоида плоскостями
плоскостями в положительном направлении относительно
внешней нормали
в положительном направлении относительно
внешней нормали параболоида.
параболоида.Убедиться в потенциальности поля
 .
.
Список литературы
Пискунов Н.С. Дифференциальное и интегральное исчисления: В 2т.-М.: Физматлит, 2000,-Т.2.-560с.
Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: В2ч.-М.: Высшая школа., 1999. ч.2-415с.
Задачи и упражнения по математическому анализу для ВТУЗов под ред. Б.П.Демидовича. М.:Изд-во «Астрель», 2003.-400с.
Гаврилов В.Ф. Кратные и криволинейные интегралы. Элементы теории поля.-M.: Изд-во МГТУ им. Баумана, 2001.-600с.
