4 Формула остроградского. Дивергенция векторного поля

Если функции дифференцируемы в замкнутой области, ограниченной кусочно-гладкой поверхностью, то имеет местоформула Остроградского

(8)

где выбрана внешняя сторона поверхности

Дивергенцией векторного поля в точке называется предел отношения потока поля через замкнутую поверхность, окружающую точкук объемутела, ограниченного этой поверхностью, при стремлении диаметратела к нулю:

.

По знаку дивергенции можно судить о наличии источника или стока векторного поля в точке . Так, еслито в точке- источник, а еслито сток. Еслито в точкенет ни источника, ни стока. Абсолютная величинахарактеризуетмощность источника или стока в точке .

Для дифференцируемых ив областисуществует

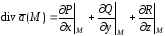(9)

в любой точке

Тогда формула Остроградского в векторной форме имеет вид

. (10)

Векторное поле называется соленоидальным в области , если его дивергенция равна нулю в каждой точке области. Для соленоидального поля характерно, что вотсутствуют источники и стоки, адля любой замкнутой поверхности.

Задача 4. Вычислить поток векторного поля через замкнутую поверхность, состоящую из частейив направлении внешней нормали (рисунок 3)

Рисунок 3

Решение. Поле дифференцируемо во всем пространстве поэтому по формуле (9) получим

и по формуле (10)

Интеграл удобно вычислять в цилиндрических координатах

Замечание. Если поверхность незамкнутая, то иногда использование формулы Остроградского в равенстве

где - еще одна поверхность, замыкающая область, может оказаться целесообразнее, чем вычисление поверхностного интеграла по поверхности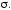

Задача 5. Вычислить поток вектора через внешнюю сторону части сферы, которая вырезана конической поверхностью(рисунок 4).

Рисунок 4

Решение. Линия пересечения сферы с конусом лежит в плоскости поэтому дополним часть сферы еще этой плоскостью и получим замкнутую поверхность. Тогда поток через часть сферыбудет получен интегралами (замечание)

где - нижняя сторона части плоскостиимеющая форму круга с границейВычислим

Здесь - проекция круга из плоскостина плоскость

5 Линейный интеграл и циркуляция векторного поля

Пусть в области задано непрерывное векторное полеи ориентированная гладкая кривая(с заданным направлением обхода). Обозначим единичный вектор касательной к линиичерез, направление которого совпадает с выбранным направлением на линии.

Линейным интегралом векторного поля вдоль линииназывается криволинейный интеграл первого рода от скалярного произведения векторови:

(11)

где - дифференциал дуги кривой.

Если ввести в рассмотрение вектор (- радиус вектор точки, описывающей линию) и обозначить его проекции на координатные оси, то формулу (11) можно записать в виде

(12)

где вектор направлен по касательной к. Правая часть равенства (12) является криволинейным интегралом второго рода (криволинейный интеграл по координатам).

Если -силовое поле, то линейный интеграл равен работе, которую поле совершает по перемещению материальной точки вдоль ориентированной линии.

Для вычисления криволинейного интеграла второго рода, если кривая задана параметрическими уравнениямии при перемещении точки отдопараметр меняется отдо(выполнение условияне обязательно), используется переход к определенному интегралу:

(13)

Линейный интеграл называется циркуляцией векторного поля , если- замкнутая линия. Тогда из двух возможных направлений обхода контураусловимся называтьположительным то, при котором область, лежащая внутри плоского контура остается слева по отношению к точке, совершающей обход (рисунок 5)

Рисунок 5

Если 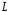- замкнутая пространственная кривая, то ее направление обхода специально оговаривается.

Задача 6. Вычислить циркуляцию поля вектора по замкнутой линии, состоящей из одного витка винтовой линииот точкидо точкии прямолинейного отрезка.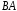

Решение. Виток соответствует изменению параметрав уравнениях кривой отдо. Прямаяимеет направляющий вектор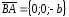, поэтому ее параметрические уравнения будут, гдеизменяется отдо. Вычислим циркуляцию по формулам (12) и (13)