Пример задачи о кратчайшем сроке.
Дан
сетевой график
:
Элементы сетевого графика
|
s дуг |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
1,2 |
1,6 |
1,7 |
2,3 |
2,7 |
6,7 |
7,3 |
7,5 |
5,3 |
3,4 |
5,4 |
6,5 |
|
|
5 |
10 |
15 |
8 |
6 |
2 |
10 |
4 |
3 |
2 |
12 |
6 |
Орграф:
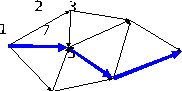
Для
каждого события i
=1,…,7 полагаем
,
шаг 1.
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 | ||||
|
|
0 |
5 |
25 |
31 |
19 |
10 |
15 | ||||
На
шаге 2 определяем новые значения величин
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 | ||||
|
|
0 |
5 |
25 |
31 |
19 |
10 |
15 | ||||
|
|
0 |
5 |
25 |
31 |
19 |
10 |
15 | ||||
На
шаге 2 ни одна из найденных величин
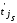не
изменяется, следовательно, полученные
при втором просмотре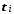
совпадают
с искомыми величинами
и
определяются самые ранние сроки
выполнения всех событий, представленных
сетевым графиком
.
Пример нахождения наиболее поздних сроков наступления событий
Лемма.
Путь
из источника (начальной вершины) в сток
(конечную вершину) в том и только том
случае является критическим, когда
соответствующим вершинам отвечают
критические события, а дугам – напряженные
работы.
Дан
сетевой график
:
Элементы сетевого графика
|
s дуг |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 | ||||||||||||
|
|
1,2 |
1,6 |
1,7 |
2,3 |
2,7 |
6,7 |
7,3 |
7,5 |
5,3 |
3,4 |
5,4 |
6,5 | ||||||||||||
|
|
5 |
10 |
15 |
8 |
6 |
2 |
10 |
4 |
3 |
2 |
12 |
6 | ||||||||||||
|
|
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 | |||||||||||||||
|
|
|
|
0 |
5 |
25 |
31 |
19 |
10 |
15 | |||||||||||||||
|
|
|
|
0 |
5 |
25 |
31 |
19 |
10 |
15 | |||||||||||||||
Положим
При
первом просмотре очередной дуги s=1,…,12
определяем новые значения по формуле
:
При втором просмотре дуг получим:
При
3-м просмотре имеем:
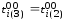
Занесем вычисленные значения в таблицу.
|
i=1,…,7 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
0 |
5 |
25 |
31 |
19 |
10 |
15 |
|
|
16 |
23 |
29 |
31 |
19 |
13 |
21 |
|
|
3 |
15 |
29 |
31 |
19 |
13 |
15 |
|
|
3 |
15 |
29 |
31 |
19 |
13 |
15 |
|
|
3 |
10 |
4 |
0 |
0 |
3 |
0 |
Так
как резервы времени
,
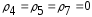то события 4, 5, 7 являются критическими.
Напряженные
работы s={3,8,11}:
s=3→(1,7):
;s=8→(7,5):
;s=11→(5,4):
;
На орграфе соответствующие дуги выделены синим цветом. Путь, содержащий эти дуги – критический. Длина критического пути равна 31.
Список литературы
Максимов Ю.А. Алгоритмы линейного и дискретного программирования. — М.: МИФИ, 1980.
Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. — М.: Мир, 1985
Н. И. Глебов , А. В. Плясунов Методы оптимизации учебное пособие
Новосибирск 2000. 105 с.