25. Мультиплексорное дерево

Максимальное число информационных входов мультиплексоров, выполненных в виде интегральных схем, равно 16. Если требуется построить мультиплексорное устройство с большим числом входов, можно объединить мультиплексоры в схему так называемого мультиплексорного дерева. Такое мультиплексорное дерево, построенное на четырехвходовых мультиплексорах, показано на рис. 2.20.

Рис. 2.20. Мультиплексорное дерево

Схема состоит из четырех мультиплексоров первого уровня с адресными переменными ,и мультиплексора второго уровня с адресными переменными,. Мультиплексорное устройство имеет 16 входов, разбитых на четверки, которые подключены к отдельным мультиплексорам первого уровня. Мультиплексор второго уровня, подключая к общему выходу устройства выходы отдельных мультиплексоров первого уровня, переключает четверки входов. Внутри четверки требуемый вход выбирается мультиплексором первого уровня. По такой схеме, используя восьмивходовые мультиплексоры, можно построить мультиплексорное устройство, имеющее 64 входа.

На первом и втором уровнях мультиплексорного дерева можно использовать мультиплексоры с разным числом входов. Если на первом уровне такого дерева используются мультиплексоры с числом адресных переменных , на втором с числом переменных, то общее число входов мультиплексорного дерева, а число мультиплексоров в схеме составит.

27. Демультиплексоры

Демультиплексоры в функциональном отношении противоположны мультиплексорам. Здесь сигналы с одного информационного входа распределяются в желаемой последовательности по нескольким выходам. Выбор нужной выходной шины, как и в мультиплексоре, обеспечивается кодом на адресных входах. При адресных входах демультиплексор может иметь в зависимости от конструкции довыходов.

Если и– адресные разряды,– информационный вход,– разрешающий (стробирующий) вход,,,,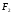– выходы, то таблица, описывающая функционирование демультиплексора 1:4, будет иметь вид (выходы инверсные)

Таблица 2.14

Адресные входы			Стробирующий сигнал		Выходы
		1		0		0	0	0
0	0	0				1	1	1
0	1	0		1			1	1
1	0	0		1		1		1
1	1	0		1		1	1

Работа устройства определяется следующими булевыми уравнениями:

; ;

; .

28. Сумматоры и полусумматоры

Полный сумматор – это устройство, предназначенное для сложения трех одноразрядных двоичных чисел ,и. Такая задача возникает при поразрядном сложении двух одноразрядных чисел, когда в качестве третьего слагаемого приходится учитывать перенос из предыдущего (младшего) разряда. Например, пусть требуется сложить два числаи. Операция сложения, как и в десятичном коде, осуществляется поразрядно от младшего разряда к старшему с учетом переполнения младшего разряда:1110 – перенос ()

+1011 –

1110 – B

11001 – сумма ()

Из примера видно, что в результате выполнения операции сложения в каждом разряде помимо суммы может образовываться перенос в очередной старший разряд. Построение функциональной схемы полного сумматора можно выполнить, записав таблицу соответствия его функционирования.

Входы					Выходы
Слагаемые			Перенос		Сумма		Перенос
0	0	0		0		0
0	0	1		1		0
0	1	0		1		0
0	1	1		0		1
1	0	0		1		0
1	0	1		0		1
1	1	0		0		1
1	1	1		1		1

Минимизировав функци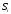и и, представленные в таблице, получим;. (2.38)

Как видно, эти функции достаточно сложны для реализации, поэтому в реальных схемах полный сумматор выполняют из двух полусумматоров. Полусумматор, в отличие от полного сумматора, обеспечивает выполнение операции суммирования двух одноразрядных двоичных чисел ибез учета сигнала переноса из младшего разряда. В результате сложения в общем случае наряду с суммой может получиться перенос. Функционирование полусумматора описывается таблицей 2.10.

0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Как видно из таблицы, для реализации необходим элемент «неравнозначность», для реализации функции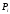– логическое И, т.е.;. (2.39)

Для упрощения схемы функцию лучше записать по нулям:(2.40)

; (2.41)

где и входи в уравнение (2.41), которое реализуется схемой, изображенной на рис. 2.14,а.

Рис. 2.14. Сумматоры

Условные графические обозначения полусумматора и полного одноразрядного сумматора приведены на рис. 2.14,б, а функциональная схема полного одноразрядного сумматора, выполненного на двух полусумматорах, – на рис. 2.14,в. Для сложения -разрядных чисел необходимоодноразрядных полных сумматоров и один полусумматор в нулевом разряде (рис. 2.14,г). В настоящее время в виде микросхем выпускаются одно- (155ИМ1), двух- (155ИМ2) и четырехразрядные (155ИМ3, 564ИМ1) двоичные сумматоры. На рис. 2.15,а показано условного графическое обозначение четырехразрядного двоичного сумматора. Входыи, где=1, 2, 3, 4 илогически равноценны.