
- •2. Сравнительная оценка базовых логических элементов
- •4. Типы корпусов микросхем
- •5. Условное графическое обозначение микросхем
- •6. Основы булевой алгебры
- •7. Аксиомы и законы булевой алгебры
- •8. Формы представления логических функций
- •12. Карты Карно для двух, трех, четырех и пяти переменных. Порядок минимизации функций с помощью карт Карно. Примеры минимизации
- •17. Комбинационные устройства: определение, методика проектирования
- •18. Шифраторы
- •19. Дешифратор
- •22, Преобразователи кодов
- •24, Мультиплексоры
- •25. Мультиплексорное дерево
- •27. Демультиплексоры
- •28. Сумматоры и полусумматоры
- •31. Многоразрядные двоичные сумматоры
- •33. Двоичные компараторы
- •35. Мажоритарный элемент
- •36. Программируемые логические матрицы
- •40. Реализация шифраторов, дешифраторов, мультиплексоров и демультиплексоров на плм
- •43. Последовательностные устройства: определение, основные типы устройств, методика проектирования
- •44. Триггеры
- •45. Классификация триггеров по функциональному назначению
- •46. Регистры
- •47. Регистры хранения
- •48. Регистры сдвига
- •49. Счетчики
- •50. Последовательные счетчики
- •51. Параллельные счетчики
- •52. Вычитающий и реверсивный счетчик
- •53. Декадный счетчик
- •64) Постоянные запоминающие устройства
- •65) Увеличение объема памяти запоминающих устройств
- •66) Назначение цап и ацп
- •67) Основные характеристики цап и ацп
- •68) Цап с матрицей взвешенных резисторов
- •69) Цап с матрицей r-2r
- •71) Области применения цап
- •72) Ацп времяимпульсного типа
- •73) Ацп с двойным интегрированием
- •74) Ацп параллельного преобразования (прямого преобразования)
- •75) Ацп последовательного счета (развертывающего типа)
- •76) Ацп следящего типа
- •77) Ацп последовательного приближения (поразрядного уравновешивания)
- •78) Области применения ацп
- •79) Схема выборки и хранения
- •85) Общая структура и принципы функционирования микропроцессорных систем
- •91. Способы адресации операндов. Особенности способов адресации.
- •92. Формат типовой команды микропроцессора. Одноадресные, двухадресные, и трехадресные команды. Классификация групп операций микропроцессора.
- •93. Команды пересылки. Команды арифметических и логических операций.
- •94. Команды сдвига. Команды сравнения и тестирования. Команды управления процессором.
- •95. Команды битовых операций. Операции управления программой.
- •96. Структурная схема, физический интерфейс и условное графическое обозначение однокристального микроконтроллера (мк) к1816ве48.
- •97) Структурная организация центрального процессора мк к1816ве48.
- •98) Организация памяти программ и данных мк к1816ве48.
- •99) Организация системы ввода-вывода мк к1816ве48.
- •100) Организация систем подсчета времени, прерываний и синхронизации мк к1816ве48.
- •101) Средства расширения памяти программ мк к1816ве48: интерфейс, схе-мы подключения, временные диаграммы.
- •102) Средства расширения памяти данных мк к1816ве48: интерфейс, схемы подключения, временные диаграммы.
- •103) Средства расширения ввода-вывода мк к1816ве48: интерфейс, схемы подключения, временные диаграммы.
31. Многоразрядные двоичные сумматоры
В
настоящее время в виде микросхем
выпускаются одно- (155ИМ1), двух- (155ИМ2) и
четырехразрядные (155ИМ3, 564ИМ1) двоичные
сумматоры. На рис. 2.15,а показано условного
графическое обозначение четырехразрядного
двоичного сумматора. Входы
 и
и ,
где
,
где =1,
2, 3, 4 и
=1,
2, 3, 4 и логически равноценны.
логически равноценны.

Рис. 2.15. Четырехразрядный двоичный сумматор
33. Двоичные компараторы
Для
сравнения операндов в цифровых системах
часто используют специальные схемы –
двоичные компараторы. Простейшим
вариантом компараторов являются схемы
для определения равенства двух операндов
 и
и .
Равенство одноразрядных операндов
определяется с помощью логической
операции «Равнозначность»:
.
Равенство одноразрядных операндов
определяется с помощью логической
операции «Равнозначность»: при
при ,
, при
при .
Для определения равенства многоразрядных
операндов выполняется конъюнкция
результатов сравнения отдельных
разрядов:
.
Для определения равенства многоразрядных
операндов выполняется конъюнкция
результатов сравнения отдельных
разрядов:
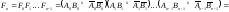
 (2.42)
(2.42)
Более
сложными являются схемы сравнения для
определения неравенства
 -разрядных
операндов
-разрядных
операндов и
и :
:

 (2.43)
(2.43)
Для
одноразрядных операндов
 и
и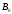 функции сравнения реализуются с помощью
операций «Запрет»:
функции сравнения реализуются с помощью
операций «Запрет»: ,
, . (2.44)
. (2.44)
Для
двухразрядных операндов
 и
и функции неравенства
функции неравенства и
и определяются таблицей истинности 2.11.
Минимизируя выражения функций с помощью
карт Карно, получаем
определяются таблицей истинности 2.11.
Минимизируя выражения функций с помощью
карт Карно, получаем
 ,
,
 . (2.45)
. (2.45)
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
0 |
1 |
|
1 |
1 |
0 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
1 |
0 |
0 |
Аналогично
представляются функции сравнения
 -разрядных
операндов:
-разрядных
операндов: , (2.46)
, (2.46)
 . (2.47)
. (2.47)
где
 ,
, – функции сравнения (
– функции сравнения (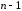 )
младших разрядов. Согласно выражениям
(2.46), (2.47) сравнение операндов можно
производить последовательно, начиная
с младших разрядов
)
младших разрядов. Согласно выражениям
(2.46), (2.47) сравнение операндов можно
производить последовательно, начиная
с младших разрядов ,
, .
Пример многоразрядного компаратора с
последовательной структурой,
реализованного в соответствии с
выражением (2.46), дан на рис. 2.18,а.
.
Пример многоразрядного компаратора с
последовательной структурой,
реализованного в соответствии с
выражением (2.46), дан на рис. 2.18,а.

В
быстродействующих компараторах
реализуется одновременное (параллельное)
сравнение всех разрядов операндов в
соответствии с выражениями (2.48), (2.49).
Эти выражения получаются из (2.46), (2.47)
подстановкой функций
 ,
…,
,
…, или
или ,
…,
,
…,

 ;
;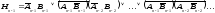
 .
.
35. Мажоритарный элемент
Мажоритарным
элементом называется пороговая схема
с нечетным числом входов
 ,
выходной сигнал которой равен 1 только
при поступлении на ее входы
,
выходной сигнал которой равен 1 только
при поступлении на ее входы или большего числа входных сигналов
или большего числа входных сигналов ,
равных 1. Мажоритарные элементы широко
используются в различного рода системах
управления при резервировании ее
элементов с целью повышения их надежности.
Выполнение таких схем на логических
элементах приводит к их большой
сложности. Более эффективно для этого
использовать сумматоры. Пример схемы
мажоритарного элемента на 13 входов (
,
равных 1. Мажоритарные элементы широко
используются в различного рода системах
управления при резервировании ее
элементов с целью повышения их надежности.
Выполнение таких схем на логических
элементах приводит к их большой
сложности. Более эффективно для этого
использовать сумматоры. Пример схемы
мажоритарного элемента на 13 входов ( )
приведен на рис. 2.17. Схема выполнена на
четырех одноразрядных
)
приведен на рис. 2.17. Схема выполнена на
четырех одноразрядных и
и ,
двух двухразрядных
,
двух двухразрядных и
и и одном четырехразрядном
и одном четырехразрядном двоичных сумматорах. На один из входов
сумматора
двоичных сумматорах. На один из входов
сумматора подан сигнал, равный 1. Тем самым порог
подан сигнал, равный 1. Тем самым порог изменяется
на
изменяется
на .
Выходной сигнал с весом 8 сумматора
.
Выходной сигнал с весом 8 сумматора будет равен 1, если семь или большее
число входных сигналов
будет равен 1, если семь или большее
число входных сигналов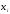 примут значения 1. Таким же способом
можно синтезировать любой мажоритарный
элемент.
примут значения 1. Таким же способом
можно синтезировать любой мажоритарный
элемент.

Рис. 2.17. Мажоритарный элемент
(2.49)






