
физ / мкт 2-2
.pdfМинистерство образования и науки Российской Федерации
Государственное образовательное учреждение высшего профессионального образования
«УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра физики
ТЕПЛОЕМКОСТЬ ИДЕАЛЬНОГО ГАЗА.
МЕТОД СТОЯЧИХ ЗВУКОВЫХ
ВОЛН ДЛЯ ОПРЕДЕЛЕНИЯ СКОРОСТИ
ЗВУКА И ОТНОШЕНИЯ CP/CV
Учебно-методическое пособие к лабораторным работам
по молекулярной физике
2-2
УФА 2010
Учебно-методическое пособие предназначено для студентов всех форм обучения и содержит краткие сведения по теории и описание порядка выполнения лабораторной работы по разделу “Молекулярная физика”.
Составители: Гусманова Г.М., доц., канд. хим. наук Сафиуллина А.Г., доц., канд. хим. наук
Рецензент |
Лейберт Б.М., доц., канд. техн. наук |
Уфимский государственный нефтяной технический университет, 2010

ЛАБОРАТОРНАЯ РАБОТА 2-2
"Теплоемкость идеального газа. Метод стоячих звуковых волн для определения скорости звука и отношения Cp/Cv"
Цель работы: изучить молекулярно-кинетическую теорию теплоемкости с помощью метода стоячих звуковых волн.
Приборы и принадлежности: стеклянная труба с миллиметровой шкалой,
емкость с жидкостью, динамик, генератор звуковых колебаний, датчик электрических колебаний, телефон.
ТЕОРИЯ МЕТОДА Внутренняя энергия представляет собой энергию всех видов
внутренних движений в теле (системе) и энергию взаимодействия всех частиц (атомов, молекул, ионов и т. д.), входящих в тело (систему). При вычислении изменения внутренней энергии учитывают ту ее часть, которая не остается постоянной в исследуемых процессах. Под внутренней энергией газа понимают кинетическую энергию движения молекул газа и потенциальную взаимодействия молекул между собой.
Идеальным газом называется газ, взаимодействиями между молекулами которого можно пренебречь. Таким образом, потенциальная энергия взаимодействия молекул идеального газа не учитывается.
Числом степеней свободы i называется число независимых координат
(уравнений), с помощью которых можно однозначно определить положение молекулы (тела) в пространстве. Для одноатомной молекулы i = 3, для двухатомной - i= 5, для трехатомной (и далее многоатомной) - i = 6.
Внутренней энергией идеального газа называется сумма кинетических энергий беспорядочного движения всех его молекул, которая равна:
U i m RT
2 M

где i - число степеней свободы, т — масса газа, М - молярная масса,
R = 8,31 Дж/(моль-К) - универсальная газовая постоянная, Т -
термодинамическая температура.
Внутренняя энергия является функцией состояния, т.е. не зависит от вида перехода из одного состояния в другое (процесса), а зависит лишь от параметров начального и конечного состояний системы.
V 2
Работа газа равна A pdV
V 1
гдер - давление, dV- бесконечно малое изменение объема.
Теплота и работа не являются функциями состояния, т.е. зависят от вида перехода из одного состояния в другое (процесса).
Первое начало термодинамики является законом сохранения энергии для тепловых процессов: количество теплоты, переданное системе,
расходуется на приращение внутренней энергии системы и совершение системой работы:
dQ = dU+dA
Иногда имеются отличия в записи малых величин теплоты, работы и приращения внутренней энергии, которые отражают зависимость теплоты
δQ и работы δА от вида перехода из одного состояния в другое (процесса), а
изменения внутренней энергии dU - только от начального и конечного состояний системы.
Теплоемкостью называется величина, равная количеству теплоты,
которое требуется передать телу, чтобы изменить его температуру на единицу (на 1К - в СИ). Единицей измерения теплоемкости является 1 Дж/К.
C dQdT
Удельной теплоемкостью называется величина, равная количеству теплоты, которое требуется передать единице массы m (1кг - в СИ) газа,
чтобы изменить его температуру на единицу (на 1К - в СИ), т. е.

теплоемкость единицы массы вещества. Единицей измерения удельной теплоемкости является 1 Дж/(кгК).
c C dQ m mdT
Молярной теплоемкостью называется величина, равная количеству теплоты, которое требуется передать единице количества вещества v (l молю в СИ), чтобы изменить его температуру на единицу (на 1К - в СИ), т. е.
теплоемкость 1 моля вещества. Единицей измерения молярной теплоемкости является 1 Дж/(моль-К).
Nm C dQ
dT
Процесс, происходящий без теплообмена с окружающей средой,
называется адиабатическим. В этом случае dQ=0, следовательно, первое начало термодинамики для него принимает вид
dU = - dA.
При этом работа совершается газом за счет убыли его внутренней энергии.
В адиабатическом процессе все термодинамические параметры р, V и Т меняются. Их можно связать уравнением Пуассона:
pVγ=const
или соотношениями TVγ-1=const, Tp(1-γ)/ γ=const
где γ- показатель адиабаты, равный Cp i 2 , - уравнениями
Cv i
адиабатического процесса.
В адиабатном процессе работу можно рассчитать по формуле:
V 2 |
V 2 |
pV |
|
pV |
|
V |
|
1 |
|
||
A |
pdV |
1 |
|
dV |
1 1 |
|
[1 ( |
1 |
) |
|
] |
V |
|
1 |
|
|
|||||||
V 1 |
V 1 |
|
|
V |
|
|
|
||||
|
|
|
|
|
|
|
|
2 |
|
|
|
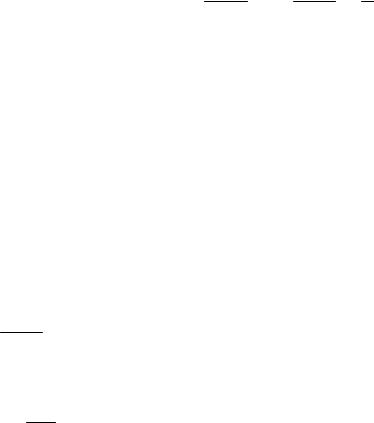
По первому началу термодинамики при постоянном объеме dA = О, и
вся подводимая системе теплота идет на увеличение его внутренней энергии,
т.е. dQ= dU. Поэтому молярная теплоемкость при постоянном объеме равна
Nv ( dQ )v dU i R
dT dT 2
По первому началу термодинамики при постоянном давлении вся подводимая системе теплота идет на увеличение его внутренней энергии и совершение работы, т.е. dQ = dU + dA. Поэтому молярная теплоемкость при постоянном давлении равна
Np ( |
dQ |
) p |
dU pdV |
Cv R |
i 2 |
R |
dT |
dT |
|
||||
|
|
2 |
|
|||
Или Cp=Cv+R.Этоуравнение называется уравнением Майера.
Молярная теплоемкость при постоянной температуре Ст равна:
NT dQdT
Молярная теплоемкость в адиабатном процессе Сад равна:
dQ
Naa dT 0
Таким образом, в молекулярно-кинетической теории теплоемкость принимает различные значения в зависимости от типа процесса.
ОПИСАНИЕ МЕТОДА
Один из доступных, достаточно точных методов определения отношения Ср /Су основан на измерении скорости распространения звука в газе. При распространении звука в газе звуковое поле представляет собой чередующиеся зоны сжатия и разрежения. В одном и том же объеме происходит последовательная смена сжатия разрежением. Звуковые волны являются достаточно высокочастотными, температура газа, претерпевающего деформацию, не успевает выравниваться с температурой других участков,
поэтому происходящие процессы можно считать адиабатическими.

Запишем волновое уравнение, которое в общем виде описывает распространение волнового процесса:
d 2 x |
V 2 |
d 2 x |
(1) |
|
dy2 |
||
dt2 |
|
||
т.е. вторая производная смещения по времени пропорциональна второй производной смещения по координате, причем коэффициентом пропорциональности служит квадрат скорости распространения волны V.
Для определения скорости распространения волны в упругой среде плотностью ρ для участка, мысленно вырезанного в сплошной среде длиной dy, поперечного сечения S, который растянут или сжат на величину dx,
воспользуемся законом Гука: |
f |
1 |
|
|
dx |
S |
(2) |
||||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
||||
где |
? |
|
- сила упругости, |
|
α - коэффициент |
упругости. |
|||||||||||
По второму закону Ньютона получим: |
|
|
|
|
|
|
|
||||||||||
|
d 2 x |
|
|
1 d 2 x |
|
|
|
|
|
|
|
|
|
(3) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
dt2 |
dy2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Сравнивая (1) и (3), получим, что |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
1 |
|
|
|
|
(4) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
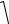
Так как коэффициент упругости а связан с модулем Юнга E по формуле
α=1/E, то перепишем (4) в виде V |
E |
(5) |
||||
|
||||||
|
|
|
|
|
||
|
По определению для деформируемого упругого стержня модуль Юнга |
|||||
равен |
E |
pn |
|
|
||
dL / L |
|
|||||
|
|
|
||||
(6)
где рп - сила, отнесенная к единице площади поперечного сечения стержня, a dL/L - относительная линейная деформация. Для столба газа рn
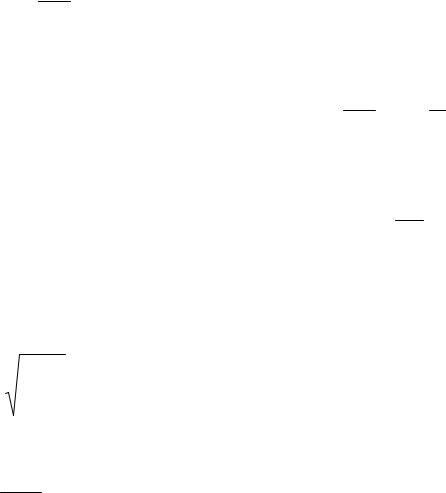
заменим на давление dp, вызывающее сжатие газа, a dL/L - на
относительную объемную деформацию dV/V и получим модуль Юнга в виде
E V dp dV
Звуковые колебания газа считаем адиабатическими, поэтому
дифференцируя уравнение Пуассона, получим dp p , где γ = Ср /Сv-
dV V
показатель адиабаты. Теперь E .
Заменим плотность газа ρ в (5) по формуле p , где R -
RT
универсальная газовая постоянная; Т - термодинамическая температура газа;
? - его молярная масса, р - давление газа. Таким образом, скорость звука (5) в
газах определим по формуле
V |
RT |
(7) |
|
|
|||
|
|
Преобразуя эту формулу найдем
V 2
RT
Таким образом, для определения показателя адиабаты достаточно знать температуру газа и определить скорость звука в нем (молярная масса газа предполагается известной). Для воздуха ?=29·10-3кг/моль.
В данной работе измеряется скорость звука в воздухе методом стоячих волн, образующихся в столбе газа, заключенного в трубе. Стоячая волна у является результатом наложения (интерференции) двух одинаковых бегущих волн у1 и у2, распространяющихся навстречу друг другу:
y= y1(x,t)+y2 (x,t)=A о sinω(t-x/V)+A 0 sinω[(t-x/V)+π]= =-2Ао sin ωx/Vcosωt,
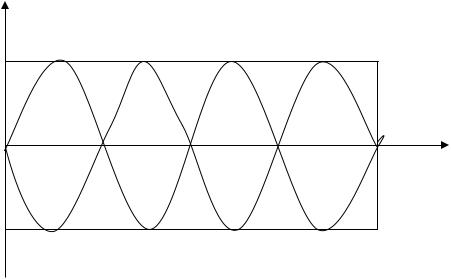
Y
A
B
X
где ω - циклическая частота, t - время, А0 - амплитуда колебаний, X -
смещение данной точки от начала координат.
В результате чего в трубе возникают точки, амплитуда которых принимает максимальные (т.А) и минимальные (т.В) значения, называемые,
соответственно, пучностями и узлами.
Координаты узлов находятся |
из |
условия |
sin ωx/V=O, |
отсюда |
|
ωx/V=±πn. |
|
|
|
|
|
Скорость звука V связана |
с |
его частотой |
v и длиной |
волны λ |
|
cоотношением V= λ v, |
|
|
|
|
(9) |
так как λ = VТ=V/ v = 2πV/ω, где |
Т |
- период колебаний. Следовательно, |
|||
координаты узлов x n=±2n λ / 4=±n λ /4, |
где п =0,1,2,... . Координаты |
||||
пучностей находятся из условия sinωx/V=1, отсюда ωx/V=±(2n+1)π/2.
Следовательно, координаты пучностей x n=±(2n+1) λ / 4, где п =0,1,2,...
Звуковые колебания в трубе, вообще говоря, очень сложны. Звуковая волна, распространяющаяся в трубе, испытывает многократные отражения от поверхности воды и верхнего торца трубки. На закрытых концах трубки всегда образуется узел. Расстояние между двумя соседними узлами находят из условия координат узлов: x n+1- x n = λ / 2. Картина резко упрощается, если

длина воздушного столба равна целому числу |
n полуволн с длиной волны λ, |
|
то |
l=n λ / 2. |
(10) |
Если условие (10) выполнено, то волна, отраженная от водной поверхности, вернувшаяся к верхнему торцу и вновь отраженная, совпадает по фазе с падающей. Совпадающие по фазе волны усиливают друг друга, в
чем можно убедиться с помощью осциллографа или на слух.
При неизменной частоте звукового генератора (а, следовательно, и
длине волны) можно изменять длину воздушного столба. Для этого в работе применяют сосуд с водой, соединенный резиновым шлангом с измерительной трубой. Поднимая или опуская сосуд, меняем длину воздушного столба, то есть длину l (см. (10)). При этом при определенных значениях l наблюдается усиление звука, в чем можно убедиться с помощью
осциллографа или на слух. Для длин воздушного столба 1п и ln+1 имеем:
1п =n λ / 2 , |
1п+1 =(n+1) λ / 2 , |
λ=2 ( ln+1-ln). |
(11) |
Используя уравнения (9) и (11), получаем
(12)
V=2ν( ln+1-ln).
ОПИСАНИЕ УСТАНОВКИ
Схема установки изображена на рис. 2. Стеклянная труба, соединенная с емкостью С, снабжена миллиметровой шкалой, по которой отсчитывается расстояние между мембраной М и уровнем жидкости, то есть l длина воздушного столба. Уровень жидкости в трубе можно изменять путем поднятия соединенной с трубой емкости С. Колебания воздуха в трубе возбуждаются под действием мембраны динамика М, питающегося от генератора электрических колебаний звуковых частот ЗГ. Вблизи динамика смонтирован датчик электрических колебаний ДК, который преобразует
