лекции по физике / Лекция 17

Лекция 17.

МЕХАНИЧЕСКИЕ ЗАТУХАЮЩИЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ЭЛЕКТРОМАГНИТНЫЕ ЗАТУХАЮЩИЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ.ВОЛНЫ.

УРАВНЕНИЕ ВОЛН.

17.1. Затухающие колебания.

На примере физического маятника и идеального (R=0) колебательного контура рассматривались собственные свободные колебания, когда энергия оставалось постоянной и колебания продолжались неограниченно долго. В реальных системах обычно действует сила трения или сила сопротивления среды. При небольших скоростях сила сопротивления пропорциональна величине скорости. Тогда уравнение свободных затухающих колебаний примет вид . (Из 2 закона Ньютона ma=-kx-rv , где r- коэффициент пропорциональности в формуле F_c=-rv )

Разделим это уравнение на массу тела и обозначим ; (- коэффициент затухания)

Тогда получим дифференциальное уравнение

(17.1)

Решением этого уравнения при условии, что , является функция

(17.2)

где -частота затухающих колебаний и определяется формулой .

Как видно, амплитуда колебаний, описываемых уравнением (17.2), уменьшается с течением времени, т.е. эти колебания являются затухающими.

График этой функции дан на рисунке 17.1. Скорость затухания колебаний определяется величиной , т.е. коэффициентом затухания.

Рассмотрим аналогичные колебания в колебательном контуре. Всякий реальный контур обладает активным сопротивлением. Энергия контура постепенно расходуется в этом сопротивлении на нагревание, поэтому

свободные колебания затухают.

Рис 17.1

Уравнение электрических колебаний в таком контуре имеет вид:

. (Из закона Киргофа U_c + U_R = ε_s )

Это уравнение получено исходя из того, что сумма падений напряжения на емкости, индуктивности и активном сопротивлении должна быть равна нулю.

Разделив уравнение на L, заменив J через , а через и, введя обозначения и , получим

(17.3)

При условии, что , т.е. решение уравнения (17.3) имеет вид:

(17.4)

где или .

Таким образом, частота затухающих колебаний меньше собственной частоты . Период затухающих колебаний .

Скорость затухания, уменьшение амплитуды А характеризуют логарифмическим декрементом затухания. Его величина определяется формулой:

(17.5)

Затухание можно также охарактеризовать еще и временем τ, за которое амплитуда уменьшается в е раз. Оно связано с коэфициентом затухания формулой β = . Сравнивая с (17.5), получим , где N_e – число колебаний, при котором амплитуда уменьшается в е раз. Для характеристики колебательной системы часто пользуются, особенно в радиотехнике, понятием добротности контура Q. Она связана с логарифмическим декрементом затухания соотношением , так как , то . Физический смысл добротности контура следует из формулы , где ΔW уменьшение энергии за период, а W – энергия в контуре . Учитывая (17.5) можно записать, что . Если затухание невелико, () можно положить .

Тогда, учитывая, что , получим

(17.5)

17.2. Вынужденные колебания. Резонанс.

Вынужденными называются такие колебания, которые возникают в колебательной системе под действием внешней периодически измкняющей ся (вынуждающей) силы.

Пусть вынуждающая сила изменяется со временем по гармоническому закону , тогда уравнение движения запишется следующим образом: .

Можно записать и виде:

(17.6)

где .

Частным решением уравнения (17.6) является функция

(17.7)

где , .

Из уравнения (17.7) следует, что под действием гармонической внешней силы вынужденные колебания совершаются по гармоническому закону с частотой , равной частоте вынуждающей силы. Явление возрастания амплитуды вынужденных колебаний при приближении циклической частоты вынуждающей силы к частоте собственных колебаний системы называется резонансом, а соответствующая частота - резонансной частотой.

Резонансная частота определяется из выражения

(17.8)

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы показана графически на рис. 17.2. Рассмотрим вынужденные электромагнитные колебания в контуре. Уравнение вынужденных колебаний получим, приравнивая сумму падений напряжения

на элементах контура к приложенному напряжению .

Перейдя от тока к заряду и воспользовавшись обозначениями, введенными ранее, получим уравнение:

Рис. 17.2 (17.9)

Частное решение этого уравнения имеет вид:

(17.10)

где ;

.

Подстановка в эти выражения для и дает:

(17.11)

Общее решение неоднородного дифференциального уравнения (17.9) получится, если к частному решению прибавить общее решение соответствующего однородного уравнения, т.е. уравнение (17.4).

Это решение содержит экспоненциальный множитель e^t, поэтому по прошествии с начала колебаний достаточного времени это решение становится очень малым и им можно пренебречь. Следовательно, установившиеся вынужденные колебания описываются функцией (17.10). (Аналогично и в случае с механическими колебаниями). Амплитуда тока имеет значение .

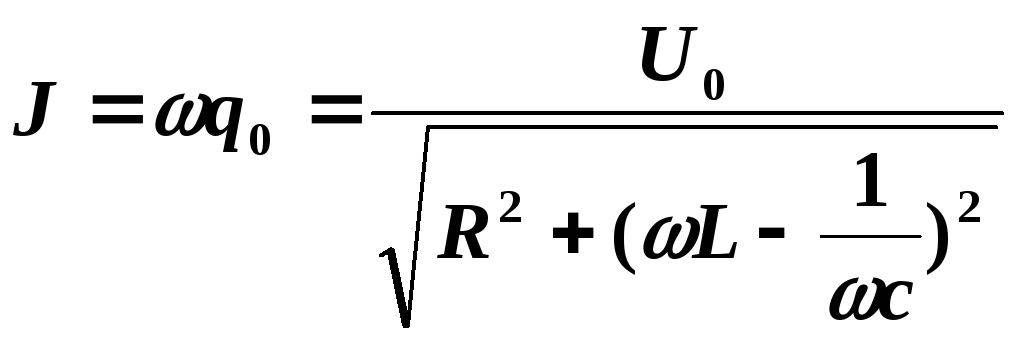Величина носит название полного сопротивления электрического контура, оно зависит от значений R , L , C и от частоты вынуждающей силы. При , удовлетворяющей соотношению

, где

где ωL - реактивное индуктивное сопротивление, - реактивное емкостное сопротивление, полное сопротивление контура достигает минимума, а амплитуда величины тока достигает максимального значения, частота носит название резонансной.

17.3 Волны. Уравнение плоской волны.

Если в каком-либо месте упругой (жидкой, твердой или газообразной) среды возбудить колебания ее частиц, то вследствие взаимодействия между частицами это колебание может распространяться в среде от частицы к частице с некоторой скоростью . Процесс распространения колебаний в пространстве называется волной или волновым движением.

Направление распространения волны (колебания) называется лучом. Волна называется поперечной, если частицы среды колеблются перпендикулярно к лучу. Если же они колеблются вдоль луча, то волна называется продольной.

Продольные волны могут возникать в среде, облапдающей упругостью объема, т.е. в твердых, жидких и газообразных телах. Поперечные волны возникают только в среде, обладающей упругостью формы, т.е. только в твердых телах. Исключение составляет волны на поверхности воды ( и вообще на поверхности раздела сред, имееющих разную плотность), где упругость формы обеспечивается силами тяжести и поверхностного натяжения.

Распространяясь от источника колебаний, волновой процесс охватывает все новые и новые части пространства. Фронт волны представляет собой ту поверхность, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли.

Геометрическое место точек, колеблющихся в одной фазе, называется волновой поверхностью. Волновые поверхности остаются неподвижными. Волновой фронт все время перемещается.

Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости или сферы. Соответственно волна в этих случаях называется плоской или сферической.

Выведем уравнение плоской волны. Его называют еще уравнением бегущей волны.

Поперечная волна распространяется по оси ОХ (Рис.17.5) от источника гармонических колебаний с частотой . В точку С на расстоянии Х колебание придет через время , (- скорость вдоль оси), тогда колебания

Рис. 17.5 частицы в этой точке опишутся уравнением

.

Это и есть уравнение бегущей волны, но чаще оно записывается в другом виде:

или

.

Отношение -

называется волновым числом и тогда уравнениние плоской волны

(17.13)

Энергия переносимая волной за единицу времени через единицу площади, называется интенсивностью волны. Она определяется формулой:

,

где W - объемная плотность энергии, V- скорость волны (вектор Умова).