29

§ 7. Линейная зависимость векторов. Базис

Определение. Векторы a1 , a2 , …, ak называются линейно зависимыми, если существуют числа λ1 , λ2 , …, λk , не все равные нулю, для которых имеет место равенство

Таким образом, если несколько векторов линейно зависимы, то хотя бы один из них всегда можно представить в виде линейной комбинации остальных.

Справедливо и обратное: если один из векторов представлен в виде линейной комбинации других векторов, то все эти векторы линейно зависимы.

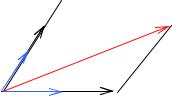
Теорема 1. Всякие три вектора на плоскости a , b и cr линейно зави-

симы.

Доказательствоr . 1) Среди векторов имеется пара коллинеарных, например, ar и b . Тогда имеем

r ar = λb , или ar = λ b + 0 cr, т.е. a есть линейная комбинация векторов b и cr, следовательно, a , b , c линейно зависимы.

2) Среди данных векторов нет ни одной пары коллинеарных. Допустим, что

30

→ = λ r

OC 2 c . Поэтому

т.е. ar является линейной комбинацией векторов b и c , следовательно, a , b и cr линейно зависимы.

Следствие 1. Если число данных векторов на плоскости больше 3, то они линейно зависимы.

Доказательство. Пусть даны векторы a1 , a2 , …, ak , k > 3. По теореме 1

имеем

a1 = μ1 a2 + μ2 a3 .

Значит

a1 = μ1 a2 + μ2 a3 + 0 a4 +... + 0 ak ,

следовательно, данные векторы линейно зависимы.

Теорема 2. Для того, чтобы два вектора a и b были линейно независимы, необходимо и достаточно, чтобы они были неколлинеарны.

Следствие 2. Максимальное число линейно независимых векторов на плоскости равно двум.

Определение. Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

Теорема 3. Всякие четыре вектора a , b , c и dr в пространстве линейно зависимы.

Доказательство. Допустим, что рассматриваемые векторы имеют общее начало. Для того, чтобы показать их линейную зависимость, достаточно убедиться в том, что один из векторов является линейной комбинацией остальных. Возможны два случая.

1) Среди данных векторов существует тройка компланарных, например, a , b

31

жет быть представленr вrвиде суммы трех векторов, коллинеарных соответст-

венно векторам b , cr и d .

Строим плоскости, проходящие через точку M (конецrвектораr a ), параллельные плоскостям, определяемым (b и cr ), (cr и d ), (b и d ). Получим

Следствие 3. Если число векторов в пространстве больше четырех, то они линейно зависимы.

Теорема 4. Для того, чтобы 3 вектора в пространстве были линейно независимы, необходимо и достаточно, чтобы они были некомпланарны.

Следствие 4. Максимальное число линейно независимых векторов в пространстве равно трем.

7.1 Базис на плоскости и в пространстве

Определение. Базисом на плоскости называются два любых линейно независимых вектора.

Из теоремы 2 следует, что два любых неколлинеарных вектора образуют на плоскости базис.

Пусть b и cr образуют на плоскости базис. Тогда для любого вектора плоскости ar имеем

32

Определение. Базисом в пространстве называются три любых ли-

нейно независимых вектора.

Из теоремы 4 следует, что всякие 3 некомпланарных вектора образуют в пространстве базис. Как и в случае плоскости, любой вектор пространства

ar однозначно разлагается по базису b , c и d :

ar = λ1 b + λ2 cr + λ3 d .

Числа λ1 , λ2 , λ3 называются аффинными координатами вектора a :

a= {λ1; λ2 ; λ3}br, cr, dr .

7.2Прямоугольный Декартов базис. Декартова система координат

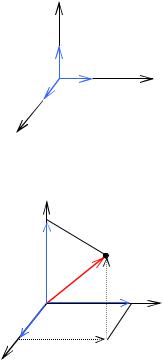
Рассмотрим в пространстве три вектора i , j , k , которые имеют еди-

ничную длину и попарно перпендикулярны. Т.к. они некомпланарны, то образуют в пространстве базис, который называют прямоугольным или Декартовым базисом. Пусть точка O – общая на-