Задачи для самоконтроля

Задача 1

Получены функции:

y = a + bx³, y = a + blnx, y = a + bx^c, y^a = b + cx², y = 1 + a(1 – x^b), y = a + bx/10.

Определите, какие из представленных выше функций линейны по переменным, линейны по параметрам, нелинейны ни по переменным, ни по параметрам.

Задача 2

Для трех видов продукции А, В и С модели зависимости удельных постоянных расходов от объема выпускаемой продукции выглядит следующим образом:

y_A = 600; y_B = 80 + 0,7x; y^C = 40x^0,5.

Определите коэффициенты эластичности по каждому виду продукции и поясните их смысл. Определите, каким должен быть объем выпускаемой продукции, чтобы коэффициенты эластичности для В и С были равны. Сравните эластичность затрат для продукции В и С при х = 1000.

Задача 3

Изучается зависимость материалоемкости продукции от размера предприятия по 10 однородным заводам (см. таблицу).

Показатель	Материалоемкость продукции по заводам
	1	2	3	4	5	6	7	8	9	10
Потреблено материалов на единицу продукции, кг., y	9	6	5	4	3,7	3,6	3,5	6	7	3,5
Выпуск продукции, тыс. ед., х	100	200	300	400	500	600	700	150	120	250

1. Найдите параметры уравнения ;

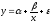2. Оцените тесноту связи с помощью индекса корреляции;

3. Охарактеризуйте эластичность изменения материалоемкости продукции;

4. Сделайте вывод о значимости уравнения регрессии.

Задача 4

Некоторая организация в течении 6 кварталов вкладывала всю прибыль в свое развитие. При этом предполагается, что прибыль растет по показательному закону у = ab^x (здесь фактор x – номер квартала, y – прибыль, млн. руб.). Составить уравнение регрессии, найти коэффициент нелинейной корреляции, и при α = 0,0.5 проверить его значимость.

xi, номер квартала	1	2	3	4	5	6
yi, прибыль, млн.руб.	1	2	5	9	15	27

Задача 5

Владелец супермаркета доставил задачу определить зависимость между средней длинной очереди в кассу (фактор y, чел.) и количеством касс, обслуживающих клиентов (фактор x, шт.). По результатам наблюдений были получены выборки значений:

xi	2	3	4	5	6	7	8
yi	45	42	37	31	23	12	3

Предполагается, что зависимость между факторами имеет вид у(х) = ах² + bх + с. Построить уравнение параболической регрессии, найти нелинейный коэффициент парной корреляции и на уровне значимости α = 0,05 проверить его значимость.

Множественная регрессия и корреляция Практическое занятие 1

Множественная регрессия – уравнение связи с несколькими независимыми переменными:

y = f(x₁, х₂, ..., х_р),

где у – зависимая переменная (результативный признак);

x₁, х₂, ..., х_р – независимые переменные (факторы).

Для построения уравнения множественной регрессии чаще используются следующие функции:

- линейная – у = а + b₁ х₁ +b₂ х₂ + ... + b_р х_р + ε;

- степенная – ;

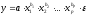- экспонента – ;

- гипербола –.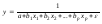

Можно использовать и другие функции, приводимые к линейному виду.

Для оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов (МНК). Для линейных уравнений и нелинейных уравнений, приводимых к линейным, строится следующая система нормальных уравнений, решение которой позволяет получить оценки параметров регрессии:

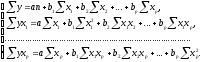
Решение системы может быть найдено по формулам Крамера:

,,…,

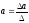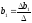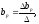
где Δ – главный определитель системы нормальных уравнений:

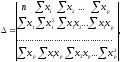
Δa, Δb₁, … Δb_p – частные определители, получаемые путем замены соответствующего столбца матрицы главного определителя системы.

Другой вид уравнения множественной регрессии – уравнение регрессии в стандаптизованном масштабе:

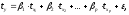
где t_y, t_x1, …,t_xp – стандартизованные переменные: 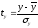, , 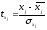для которых среднее значение равно нулю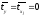, а среднее квадратическое отклонение равно единице:;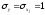

βj – стандартизованные коэффициенты регрессии, которые показывают, на какую часть своего среднего квадратического отклонения σ_y (или на сколько σ_y) изменится результат у с увеличением соответствующего фактора x_j на величину своего среднего квадратического отклонения σ_xj при неизменномсреднем уровне других факторов, оказывающих влияние на у.

К уравнению множественной регрессии в стандартизованном масштабе применим МНК. Стандартизованные коэффициенты регрессии (β-коэффициенты) определяются из следующей системы уравнений:

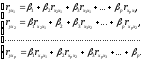
Связь коэффициентов множественной регрессии b_i со стандартизованными коэффициентами βj описывается соотношением:

, .

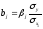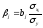Параметр а определяется по формуле:

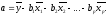
Средние коэффициенты эластичности для линейной регрессии показывают, на сколько процентов в среднем изменится результат у при изменении соответствующего фактора x_i на 1%, и рассчитываются по формуле:

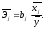
Данные показатели эластичности можно сравнивать между собой и, тем самым, ранжировать факторы по силе их воздействия на результат.

Частные коэффициенты эластичности рассчитываются по формуле:

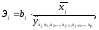
где b_j – коэффициенты регрессии для фактора хj в уравнении множественной регрессии;

–частное уравнение регрессии, которое связывает результативный признак у с соответствующими факторами х при закреплении фактора xj на среднем уровне.