
- •Содержание
- •Силы, действующие в жидкости. Давление
- •Основные физические свойства жидкостей и газов
- •Плотность и удельный вес
- •Вязкость
- •Сжимаемость
- •Температурное расширение
- •Раздел 1. Основы гидростатики
- •Тема 1.1 Основы гидростатики
- •Способы измерения давления
- •Сила давления на плоскую стенку
- •Сила давления на криволинейные стенки. Плавание тел
- •Относительный покой жидкости
- •Тема 1.2 Основы гидродинамики Основные понятия и определения
- •Расход. Уравнение расхода
- •Уравнение Бернулли для струйки идеальной жидкости
- •Уравнение Бернулли для потока реальной жидкости
- •Экспериментальная (графическая) иллюстрация уравнения Бернулли
- •Основы гидродинамического подобия
- •Режимы течения жидкости
- •Течение капельной жидкости с кавитацией
- •Тема 1.3 Гидравлические машины. Общие сведения о гидросистемах
- •Гидромашины, их общая классификация и основные параметры.
- •Объемный гидропривод, принцип действия и основные понятия
- •Струйные насосы
- •Центробежные насосы
- •Коэффициенты полезного действия центробежного насоса
- •Шестеренные насосы Гидравлические машины шестеренного типа
- •Пластинчатые насосы и гидромоторы
- •Раздел 2.
- •Работа расширения или сжатия газа
- •Термодинамические процессы: изохорный, изобарный, изотермический, адиабатный, политропный
- •Адиабатный процесс
- •Политропный процесс
- •Тема 2.2 Термодинамические циклы, использование в промышленных установках.
- •Дизельные
- •Газовые
- •Газодизельные
- •Роторно-поршневой
- •Двухступенчатая холодильная машина
- •Тема 2.3 Основные элементы пневматических систем
- •Принципы построения пневмосистем
- •Раздел 3 Элементы гидравлического и пневматического привода. Комбинированные системы.
- •Список используемой литературы
Адиабатный процесс
Адиабатный процесс – это процесс, при котором рабочее тело не обменивается теплотой с окружающей средой (dq=0). Для получения графика процесса в p-v координатах выполним некоторые преобразования.
В соответствии с первым законом термодинамики, где с – теплоёмкость термодинамического процесса. Тогда можно записать, что
(7.40)
![]()
Продифференцируем уравнение состояния идеального газа и запишем
(7.41)

Так как R=cp-cv, то выражение (7.41) можно переписать с учётом (7.42) следующим образом:
(7.42)

![]() Выполним
преобразования выражения
Выполним
преобразования выражения
|
|
|
|
|
|
|
|
(7.44) |
|
|
(7.45) |
Обозначим
 ,
тогда
,
тогда
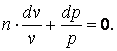
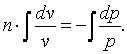
|
|
|
|
|
|
|
|
|
С
|
|
(7.46) |
В
адиабатном процессе dq=0,
то есть c·dT=0.
Поэтому c=0.
Значит в адиабатном процессе
 .
Эту величину принято обозначать буквой
.
Эту величину принято обозначать буквой
![]() и
называть показателем адиабаты.
и
называть показателем адиабаты.
П
Рис.
7.12 График адиабатного процесса
в p-v
координатах

Запишем
для точек 1 и 2 уравнения состояния Так
как в адиабатном процессе
p1·v1k=p2·v2k,
то
 ,
,  ,
,
 .
.
Приращение внутренней энергии газа .
Так
как
![]()
 ,
а
,
а
![]() ,
то
,
то
 ,
а
,
а
 .
.
Поэтому

Работа газа в адиабатном процессе выполняется за счёт его внутренней энергии. Так как в адиабатном процессе отсутствует обмен теплотой с окружающей средой, то в соответствии с первым законом термодинамики имеем l+Δu=0 или l=-Δu. Поэтому
|
|
|
|
|
(7.48) |
Изменение энтальпии газа в адиабатном процессе может быть определено исходя из следующих соображений:
|
|
|

Так как, то в итоге получим
(7.49)
![]()
Энтропия газа в адиабатном процессе не изменяется, так как dq=0. Поэтому в T-s координатах адиабатный процесс изображается прямой линией, параллельной оси температур.
Политропный процесс
Политропным процессом называется любой произвольный процесс изменения состояния рабочего тела, происходящий при постоянной теплоёмкости сп.
Для
получения графика политропного процесса
в p-v
координатах будем придерживаться тех
же рассуждений, что и при получении
графика адиабатного процесса. Заменим
в соотношениях, полученных при изучении
адиабатного процесса, обозначение
теплоёмкости с
на сп
и обнаружим, а
 .
В дальнейшем всё, что написано об
адиабатном процессе, можно распространить
на описание политропного процесса,
заменяя в выражениях k
на n.
.
В дальнейшем всё, что написано об
адиабатном процессе, можно распространить
на описание политропного процесса,
заменяя в выражениях k
на n.
Покажем, что адиабатный процесс делит все процессы на две группы: на процессы, в которых теплоёмкость больше нуля, и на процессы, в которых теплоёмкость меньше нуля.
Так
как
 ,
то можно записать
,
то можно записать
![]() ;
;
![]() ;
;
![]() ;
;
 .
.
Из последнего выражения видно, что при n>k cп>0, а при k>n>1 cп<0.
В заключение отметим, что все рассмотренные ранее процессы – это частные случаи политропного процесса.
При n=k имеем адиабатный процесс.
При n=0 имеем р1·v10=р2·v20, то есть изобарный процесс (p1=p2).
При n=1 имеем р1·v1= р2·v2, то есть изотермический процесс.
При n=∞ имеем
![]()
или
 ,
что равносильно
,
что равносильно
![]()
или
![]() ,
то есть изохорный процесс.
,
то есть изохорный процесс.





