7.1.3 Воксельная модель

Воксельная модель – это трехмерный растр. Воксел это элемент объема. По аналогии с 2D растрами, состоящими из пикселов. Вокселы заполняют объем в трехмерном растре (рис.7.9)

Рис. 7.9. Пикселы и вокселы

Как мы знаем, любой пиксел должен иметь свой цвет. Любой воксел также имеет свой цвет, и, кроме того, прозрачность. Полная прозрачность воксела озна­чает пустоту соответствующей точки объема.

Поскольку вокселы располагаются в узлах равно­мерной сетки, то, обычно, чем меньше шаг сетки, тем большее количество вокселов помещается в опреде­ленном объеме, и тем меньший размер каждого от­дельного воксела. Основная характеристика вексель­ной модели — разрешающая способность — количест­во вокселов в определенном объеме. Она и определяет точность моделирования трехмер­ных объектов (рис. 7.10).

Для современной КГ вексельный метод считается одним из перспективных. Его исполь­зуют в компьютерных системах, предназначенных для медицинских целей.

Например, при сканировании томографом (computed tomography) получаются изображения срезов объекта, которые потом объединяются в виде объемной модели для дальнейшего анализа. Ве­ксельный метод используется в геологии, сейсмологии, в компьютерных играх. Во­кселы также используются для графических устройств отображения, которые создают дей­ствительно объемные изображения.

Положительные черты воксельной модели:

• достаточно простое описание сложных объектов и сцен;

• простая процедура отображения объемных сцен;

• простое выполнение топологических операций над отдельными объектами и сценой в целом. Например, просто выполняется показ разреза — для этого соответствующие вокселы можно сделать прозрачными.

Рис. 7.10. Воксельная модель шара и ее разрезы.

Недостатки воксельной модели:

• большое количество информации, необходимой для представления объемных данных. Например, объем 256x256x256 имеет небольшую разрешающую способность, но требует свыше 16 миллионов вокселов;

• значительные затраты памяти ограничивают разрешающую способность, точность моделирования;

• большое количество вокселов обуславливает маленькую скорость создания изображений объемных сцен;

• как и для любого растра, возникают проблемы при масштабировании — увеличении или уменьшении.

7.1.4 Равномерная сетка

Эта модель описывает координаты отдельных точек поверхности следующим способом (рис. 7.11). Каждому узлу сетки с индексами (i,j) приписывается значение высотыz_i,j. Ин­дексам (i,j) соответствуют определенные значения координат (х,у). Расстояние между уз­лами одинаковое —dx по оси х иdyпо оси у.

Фактически, такая модель является двумерным массивом (растром, матри­цей), каждый элемент которой хранит значение высоты.

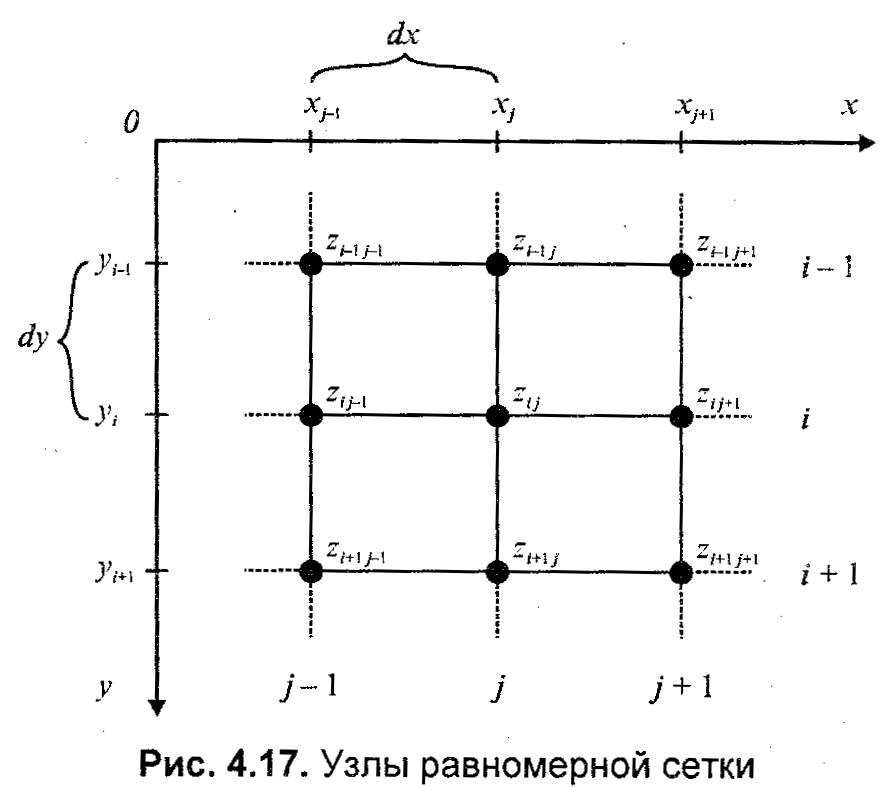
Рис. 7.11. Узлы равномерной сетки

Рис. 7.12. Точка в сетке с координатами (x, y, z)

Не каждая поверхность может быть представлена этой моделью. Если в каж­дом узле записывается только одно зна­чение высоты, то это означает, что по­верхность описывается однозначной функцией z=f(xy). Иначе говоря, это такая поверхность, которую любая вер­тикаль пересекает только один раз. Не могут моделироваться также вертикаль­ные грани. Следует отметить, что для сетки не обязательно использовать толь­ко декартовы координаты. Например, для того, чтобы описать поверхность шара однозначной функцией, можно использо­вать полярные координаты. Равномерная сетка часто ис­пользуется для описания рельефа земной поверхности.

Рассмотрим, как можно рассчитать значение высоты для любой точки внутри границ сетки. Пусть ее координаты равняются (х, у). Надо найти соответствующее значение z. Решение этой задачи — интерполяция значений координат 2 ближайших узлов (рис 7.12).

Сначала необходимо вычислить индексы i и j одного из узлов:

где ]а[ — целая часть числаа, то есть наибольшее целое, которое не превышаета.

Далее используем, например, билинейную интерполяцию. Для этого сначала найдем значенияг в точкахА и В. Из пропорции

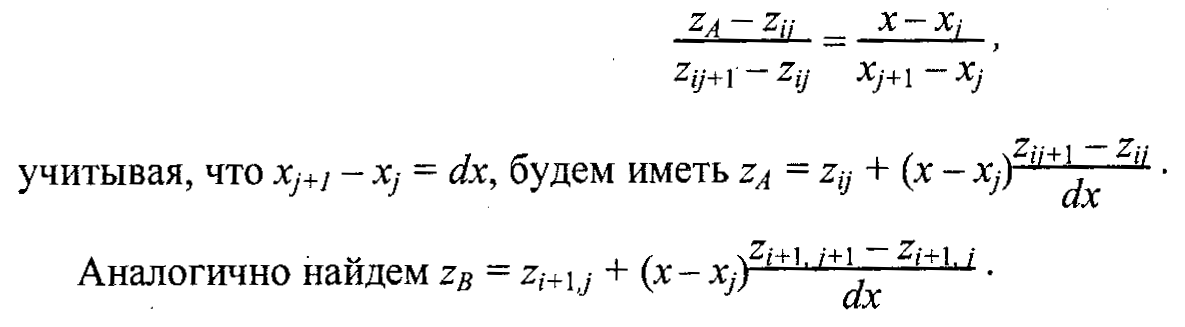
учитывая, что x_j+1 - x_j = dx, будем иметь:

Аналогично найдем

Теперь нужно вычислить такое значение z, поделив отрезок АВ пропорционально значению у:

И будем иметь: z = z_А + (y – y_i)

Положительные черты равномерной сетки:

1. Простота описания поверхностей

2. Возможность быстро узнать высоту любой точи поверхности простой интерполяцией.

Недостатки равномерной сетки:

1. Поверхности, которые соответствуют неоднозначной функции высоты в узлах сетки, моделироваться не могут

2. Для описания сложных поверхностей нужно большое количество узлов, которое может быть ограничено объемом памяти компьютера

3. Описание отдельных типов поверхностей может быть более сложным, чем в других моделях. Например, многогранная поверхность требует избыточный объем данных для описания в сравнении с полигональной моделью.