2.2.2 Основные типы проекций

Изображение объектов на плоскости (экране дисплея) связано с геометрической операцией проектированием. В компьютерной графике используется несколько видов проектирования, но основных - два вида: параллельное и центральное.

Проектирующий пучок лучей направляется через объект на картинную плоскость, на которую в дальнейшем находят координаты пересечения лучей (или прямых) с этой плоскостью.

Рис. 2.14. Основные типы проекций

При центральном проектировании все прямые исходят из одной точки.

При параллельном - считается, что центр лучей (прямых) бесконечно удален, а прямые параллельны.

Каждый из этих основных классов разбивается еще на несколько подклассов в зависимости от взаимного расположения картинной плоскости и координатных осей.

Перспективные (центральные) проекции

Одноточечная проекция

Рис. 2.15. Классификация плоских проекций

У параллельных проекций центр проекции расположен в бесконечности от плоскости проекции:

• ортографические (ортогональные),

• аксонометрические (прямоугольные аксонометрические) - проекторы перпендикулярны к плоскости проекции, расположенной под углом к главной оси,

• косоугольные (косоугольные аксонометрические) - плоскость проекции перпендикулярна к главной оси, проекторы расположены под углом к плоскости проекции.

У центральных проекций центр проекции находится на конечном расстоянии от плоскости проекции. Имеют место так называемые перспективные искажения.

Ортогональные проекции (основные виды)

Рис. 2.16. Ортогональные проекции

1. Вид спереди, главный вид, фронтальная проекция, (на заднюю грань V),

2. Вид сверху, план, горизонтальная проекция, (на нижнюю грань H),

3. Вид слева, профильная проекция, (на правую грань W),

4. Вид справа (на левую грань),

5. Вид снизу (на верхнюю грань),

6. Вид сзади (на переднюю грань).

Матрица ортогональной проекции на плоскость YZвдоль оси Х имеет вид:

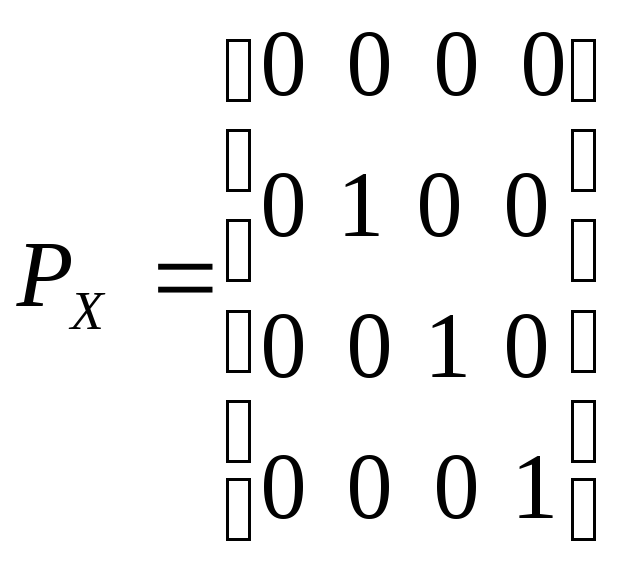
Если же плоскость параллельна, то эту матрицу надо умножить на матрицу сдвига, тогда:

где р - сдвиг по оси Х;

Для плоскости ZXвдоль осиY

гдеq- сдвиг по осиY;

Для плоскости XYвдоль осиZ:

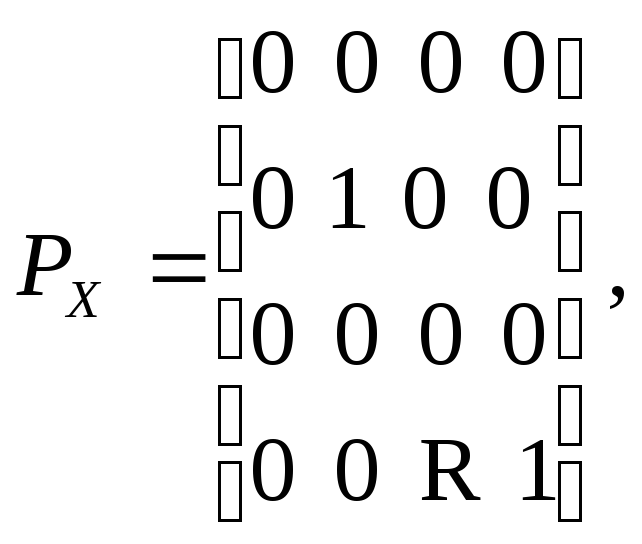гдеR- сдвиг по осиZ.

При аксонометрической проекции проектирующие прямые перпендикулярны плоскости картинки.

Изометрия- все три угла между нормалью картинки и координатными осями равны.

Диметрия - два угла между нормалью картинки и координатными осями равны.

Триметрия -нормальный вектор плоскости картинки образует с координатными осями различные углы.

Каждый из трех видов этих проекций получается комбинацией поворотов, за которой следует параллельное проектирование.

При повороте на угол β относительно оси у (ординат), на угол α вокруг оси х (абсцисс) и последующем проектировании осиZ (аппликат) возникает матрица

Изометрическая проекция

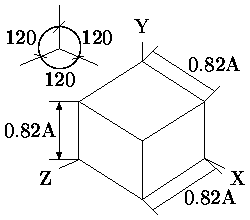
Рис. 2.17. Изометрические проекции

Диметрическая проекция

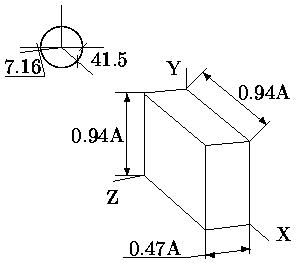
Рис. 2.18. Диметрические проекции

Косоугольные проекции

Классический пример параллельной косоугольной проекции — кабинетная проекция (рис. 2. 26). Эта проекция часто используется в математической литературе для черчения объемных форм. Осьу изображается наклоненной под углом 45 градусов. Вдоль осиу масштаб 0. 5, вдоль других осей — масштаб 1. Запишем формулы вычисления координат плоскости проецирования

Здесь, как и раньше, ось Υ_пр направлена вниз.

Для косоугольных параллельных проекций лучи проецирования не перпендикулярны плоскости проецирования.

Рис. 2.19. Косоугольные проекции

Теперь относительно центральной проекции. Поскольку для нее лучи проецирования не параллельны, то будем считать нормальной такуюцентральную проекцию, главная ось которой перпендикулярна плоскости проецирования. Дляцентральной косоугольной проекции главная ось не перпендикулярна плоскости проецирования.

Рассмотрим пример центральной косоугольной проекции, которая показывает параллельными линиями все вертикальные линии изображаемых объектов. Расположим плоскость проецирования вертикально, ракурс показа зададим углами а, β и положением точки схода (рис. 2. 21).

Рис.2.20. Кабинетная проекция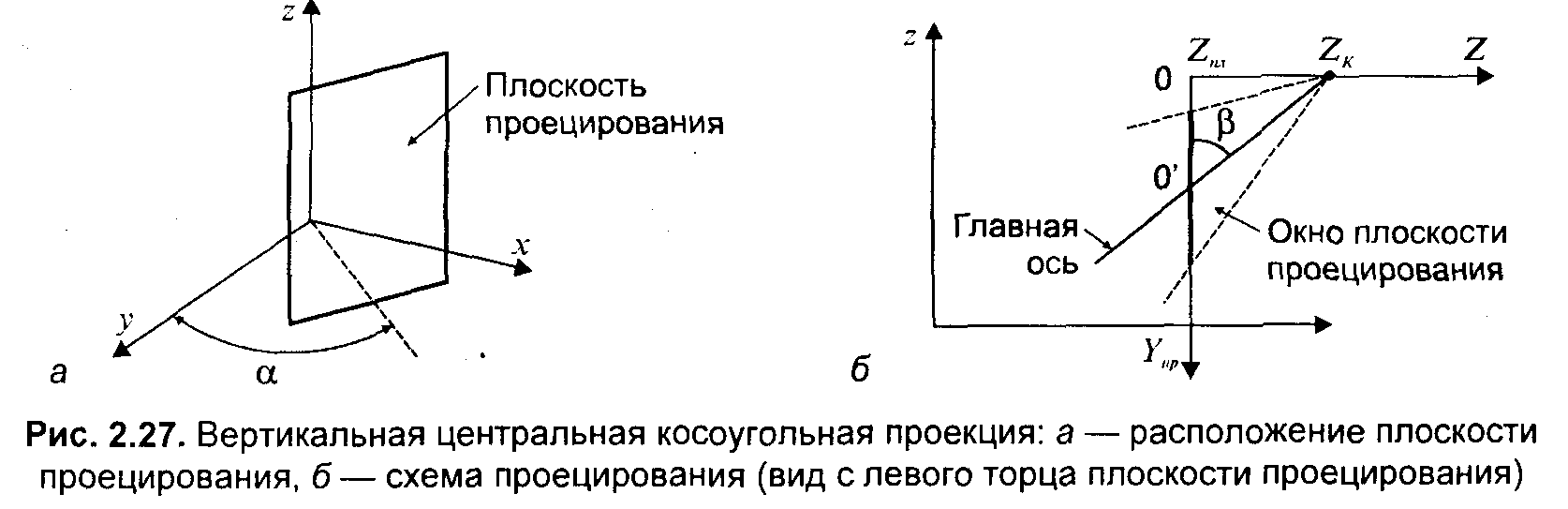

Рис. 2.21. Вертикальная центральная косоугольная проекция: а – расположение плоскости проецирования, б – вид с левого торца плокости проецирования

Будем считать, что ось Ζ видовых координат располагается перпендикулярно плоскости проецирования. Центр видовых координат — в точке (хс,ус, zc). Запишем соответствующее видовое преобразование:

Как и для нормальной центральной проекции, точка схода лучей проецирования располагается на оси Ζ на расстоянииΖ_k от центра видовых координат. Необходимо учесть наклон главной оси косоугольной проекции. Для этого достаточно отнять отΥ_пр длину отрезка 0-0' (рис. 2.21). Эта длина равняется(Ζ_k - Ζ_пл) ctgβ.Теперь запишем результат — формулы вычисления координат косоугольной вертикальной проекции

где Пх иПу — это функции проецирования для нормальной проекции.

Следует отметить, что для такой проекции нельзя сделать вид сверху (β = 0), поскольку здесьсtgP=∞.

Свойство рассмотренной вертикальной косоугольной проекции, заключающееся в сохранении параллельности вертикальных линий, иногда полезно, например, при изображении домов в архитектурных компьютерных системах. Сравните рис. 2. 22 (верх) и рис. 2.22 (низ). На нижнем рисунке вертикали изображаются вертикалями — дома не "разваливаются".

Рис. 2.21. Сравнение проекций

Кабинетная проекция (аксонометрическая косоугольная фронтальная диметрическая проекция)

Рис. 2.23.Кабинетная проекция

Свободная проекция (аксонометрическая косоугольная горизонтальная изометрическая проекция)

Рис. 2.24.Свободная проекция

Центральная проекция

Центральные проекции параллельных прямых, не параллельных плоскости проекции, сходятся в точкесхода.

В зависимости от числа координатных осей, которые пересекает плоскость проекции, различаются одно, двух и трехточечные центральные проекции.

Рис. 2.25. Центральная проекция

Рассмотрим пример перспективной (центрально) проекции для вертикального расположения камеры, когда α=β= 0. Такую проекцию можно себе представить как изображение на стекле, через которое смотрит наблюдатель, расположенный сверху в точке (х, у, z) = (0, 0,z_k). Здесь плоскость проецирования параллельна плоскости(х 0у), как показано на рис. 2. 26.

Для произвольной точки пространства (Р), исходя из подобия треугольников, запишем такие пропорции:

X_пр/(z_k – z_пл) = x/(z_k – z)

Y_пр /(z_k – z_пл) = y/(z_k – z)

Найдем координаты проекции, учитывая также координату Ζпр:

Запишем такие преобразования координат в функциональном виде

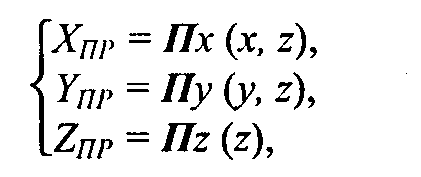
где Π — функция перспективного преобразования координат.

Рис. 2.26.Перпективная проекция

В матричной форме преобразования координат можно записать так:

Обратите внимание на то, что здесь коэффициенты матрицы зависят от координаты z (в знаменателе дроби). Это означает, что преобразование координат — нелинейное (а точнее,дробно-линейное), оно относится к классупроективных преобразований.

Мы получили формулы вычисления координат проекции для случая, когда точка схода лучей находится на оси z. Теперь рассмотрим общий случай. Введем видовую систему координат{X, Υ, Ζ), произвольно расположенную в трехмерном пространстве(х, у, z). Пусть точка схода находится на осиΖ видовой системы координат, а направление обзора — вдоль осиΖ противоположно ее направлению. Будем считать, что преобразование в видовые координаты описывается трехмерным аффинным преобразованием

После вычисления координат (X, Y, Z) можно вычислить координаты в плоскости проецирования в соответствии с формулами, уже рассмотренными нами ранее. Поскольку точка схода находится на осиΖ видовых координат, то

Последовательность преобразования координат можно описать так:

Такое преобразование координат позволяет моделировать расположения камеры в любой точке пространства и отображать в центре плоскости проецирования любые объекты обзора.

Рис. 2.27. Центральная проекция точки P₀ в плоскость Z = d