
Основы высшей математики_Гусак, Бричикова_2012 -208с
.pdfФункция распределения для дискретной случайной величины
имеет вид F ( x ) = ∑ Ρ(X = xk ) , где символы xk < x означают, что
xk<x
суммируются вероятности тех значений, которые меньше х. Функция F ( x ) для дискретной случайной величины является разрывной.
Плотность распределения
Рассмотрим непрерывную случайную величину Х, функция распределения которой F ( x ) определена в интервале (α, β) и имеет не-
прерывную производную. Зафиксируем в интервале (α, β) |
точки х |
||||
и x + x ( |
x > 0) . Равенство Ρ(α ≤ X ≤β) = F (β) −F (α) примет вид |
||||
|
Ρ( x ≤ X < x + x ) = F ( x + x ) −F ( x ) |
|
|||
Разделим это равенств на длину |
x отрезка [x, x + x] : |
|
|||
|
Ρ( x ≤ X < x + |
x ) = |
F ( x + x ) −F ( x ) |
|
(I) |
|
x |
x |
|||
|
|
|
|||
Частное |
Ρ( x ≤ X < x + x ) |
называют средней плотностью вероят- |
|||
|
x |
|
|
|
|
ностей на данном отрезке. Плотностью распределения непрерывной случайно величины в точке х называют предел средней плотности при x → 0 . Плотность распределения в точке х обозначим p( x ), тогда
p( x ) = lim |
Ρ( x ≤ X < x + x ) . |
x→0 |
x |
Каждому значению x (α, β) соответствует определенное значение этого предела; получена функция p( x ) – плотность распределения вероятностей непрерывной случайной величины Х. График функции p( x ) называют кривой распределения. Плотность распределения называют также дифференциальной функцией распределения, или дифференциальным законом распределения.
Если в равенстве (I) перейти к пределам, то получим p( x )=F′( x ). Следовательно, производная функции распределения равна плотности распределения.
Вероятность попадания значений случайной величины Х в полуинтервал [a, b) равна определенному интегралу от плотности распределения p( x ) по отрезку [a, b] :
b
Ρ(a ≤ X < b) = ∫ p( x )dx.
a
170
С в о й с т в а ф у н к ц и и p( x ) – п л о т н о с т и р а с п р е д е л е н и я
1.Функция p( x ) является неотрицательной: p( x ) ≥ 0.
2.В точках дифференцируемости F ( x ) выполняется равенство
F ′( x ) = p( x ) .
3.Интеграл по бесконечному промежутку (−∞, + ∞) от плотности
+∞
распределения p( x ) равен единице: ∫ p( x )dx =1 .
−∞
Математическое ожидание случайной величины
Если случайная величина Х принимает конечное множество значений x1, x2, ..., xn соответственно с вероятностями p1, p2, ..., pn , то ее математическим ожиданием называют сумму произведений значений на их вероятности и обозначают M (X ) .
n
M (X ) = x1p1 + x2 p2 +... + xn pn , M (X ) = ∑ xi pi .
i=1
Употребляются и другие обозначения: EX , а, mx , m.
В случае случайной величины, принимающей счетное множество значений x1, x2, x3 ... , соответственно с вероятностями p1, p2, p3, ... :
∞
M (X ) = ∑ xi pi ,
i=1
если этот ряд сходится абсолютно.
Математическое ожидание непрерывной случайной величины Х, все значения которой принадлежат отрезку [α, β] , определяется формулой
β
M (X ) = ∫ xp( x )dx.
α
Если случайная величина Х может принимать любые значения из промежутка (−∞, + ∞) , то
+∞
M (X ) = ∫ xp( x )dx,
−∞
где p( x ) – плотность распределения, при условии, что интеграл сходится.
Математическое ожидание называют средним значением случайной величины, а также центром распределения.
С в о й с т в а м а т е м а т и ч е с к о г о о ж и д а н и я 1. Математическое ожидание заключено между наименьшим зна-
чением а величины и наибольшим значением b: a ≤ M (X ) ≤ b .
2. Математическое ожидание постоянной равно этой постоянной:
M (C ) =C .
171
3.Постоянный множитель можно выносить за знак математического ожидания: M (CX ) =CM (X ).
4.Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:
M (X +Y ) = M (X ) +M (Y ) .
5. Математическое ожидание произведения двух н е з а в и с и - м ы х случайных величин равно произведению их математических
ожиданий:
M (XY ) = M (X ) M (Y ).
Свойства 4 и 5 распространяются на n случайных величин X1, X2, ..., Xn .
Отклонением случайной величины называют разность X − M ( X ). Математическое ожидание отклонения равно нулю:
M (X −M (X )) = M (X ) −M (M (X )) = M (X ) −M (X ) = 0 .
Дисперсия случайной величины
Дисперсией (или рассеянием) случайной величины Х называют математическое ожидание квадрата ее отклонения:
D(X ) = M ((X −M (X ))2 ) , D(X ) = M (X2 )−(M (X ))2 . С в о й с т в а д и с п е р с и и
1.Дисперсия постоянной величины равна нулю: D(C ) = 0 .
2.Постоянный множитель можно выносить за знак дисперсии,
возводя его в квадрат: D(CX ) =C2D(X ) .
3.Дисперсия суммы двух независимых величин равна сумме их дисперсий: D(X +Y ) = D(X ) +D(Y ) .
4.Дисперсия разности двух независимых величин равна сумме их
дисперсий; D(X −Y ) = D(X ) +D(Y ) .
Выражения для дисперсии при соответствующем законе распределения (Х принимает конечное множество значений, счетное множество, является непрерывной: обозначения: a = M (X ), p( x ) – плотность распределения):
n
D( X ) = ∑ ( xk −a)2 pk ;
k=1
∞
D( X ) = ∑ ( xk −a)2 pk
k=1
при условии, что ряд сходится;
+∞
D(X ) = ∫ ( x −a)2 p( x )dx ,
−∞
если этот интеграл сходится.
172

Средним квадратическим отклонением σ(X ) случайной величины Х называют корень квадратный из ее дисперсии.
σ(X ) = D(X ) .
Некоторые другие числовые характеристики
Ковариацией двух случайных величин Х и Y называют математическое ожидание произведения их отклонений
cov ( X, Y ) = M ((X − M ( X )) (Y − M (Y ))) . Для ковариаций верны равенства:
cov ( X, Y ) = M ( XY ) − M ( X ) M (Y ), cov ( X, X ) = D( X ), cov ( X, Y ) = cov (Y, X ), D( X +Y ) = D( X ) + D(Y ) +2cov ( X, Y ).
Если случайные величины независимы, то cov ( X, Y ) = 0 . Если cov ( X, Y ) ≠ 0 , то случайные величины зависимы.
Коэффициент корреляции ρ( X, Y ) случайных величин Х, Y опре-
деляется формулой ρ( X, Y ) = cov ( X, Y ) .
σ( X )σ(Y )
С в о й с т в а к о э ф ф и ц и е н т а к о р р е л я ц и и: 1) ρ( X, Y ) ≤1 ; 2) если величины Х и Y независимы, ρ( X, Y ) = 0; 3) если Y = AX + B, то ρ( X, Y ) =1.
Начальным моментом kEго порядка случайной величины Х называют число νk , определяемое формулой νk = M (X k ), а центральным моментом – число Mk = M (( X −a)k ) . Математическое ожидание
и дисперсия случайной величины Х – частные случаи моментов:
ν1 = M (X ), M2 = D(X ).
Некоторые законы распределения случайных величин
Вероятность того, что в серии из n испытаний событие А появится ровно k раз (и не появится n – k раз) выражается формулой Бернулли.
Ρk,n |
=Cnk pkqn−k , где Cnk = |
n(n −1)...(n −(k −1)) |
, или Cnk = |
n! |
|
, |
|
k! |
k!(n −k)! |
||||||
|
|
|
|
||||
где р – вероятность события А, q – вероятность события A (q=1− p). Закон распределения дискретной случайной величины, определяемый формулой Бернулли, называют биномиальным. Для этого за-
кона M (X ) = np, D(X ) = npq , σ(X ) = npq .
173

|
|
|
|
|
|
|
Геометрическим распределением |
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
называют распределение, определяе- |
||||
|
|
|
|
|
|
мое формулой P ( X = m)= (1− p)m−1 p |
||||
|
|
|
|
|
|
(0 < p <1) , m =1, 2, 3, ... . Для такого |
||||
|
|
|
|
|
|
распределения |
M (X ) = |
1 |
, D( X ) = |
|
|
|
|
|
|
p |
|||||
|
|
|
|
|
|
= (1− p) . |
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
p2 |
|
|
|
|
|
|
|
|
|
|
Случайную |
величину |
называют |
|
|
|
|
Рис. 13.4 |
|
равномерно распределенной на отрез- |
|||||
|
|
|
|
ке |
[α, β] , если |
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
1 |
, α ≤ X ≤ β; |
|
|
|
|
|
|
|
p( X ) = |
|
|
|
|
|
|
|
|||
(β−α) |
|
|
|
|
|
|
||||
|
|
|
X < α, X > β. |
|
|
|
|
|||
|
0, |
|
|
|
|
|
||||
|
В этом случае M (X ) = |
(α+β) , |
D(X ) = (β−α)2 . |
|
||||||
|
|
|
|
|
2 |
12 |
|
|
|
|
Нормальным распределением (или распределением Гаусса) назы-
вают распределение случайной величины Х, определяемое формулой
|
|
1 |
−(x−a)2 |
|
|
P ( X ) = |
|
e 2σ2 |
(σ > 0) , |
||
σ |
2π |
||||
|
|
|
где a = M (X ) , σ2 = D( x ). График функции P (X ) называют нормальной кривой или кривой Гаусса. На рис. 13.4 изображены три кривых при одном и том же а и различных σ.
Для нормального распределения
P (α < X <β) = Φ(β−σα)−Φ(ασ−a ),
|
|
x |
t2 |
|
|
где Φ(X ) – функция Лапласа Φ( x ) = |
1 |
∫ e− |
2 |
dt . |
|
2π |
|||||
|
0 |
|
|
Правило трех сигм выражается равенством
P ( X −a < 3σ) = 0,9973 .
(Модуль отклонения нормальной величины не превышает утроенного среднего квадратичного отклонения).
174

13.4. Комбинаторика и вероятность
Комбинаторика изучает способы подсчета числа элементов в конечных множествах. Формулы комбинаторики используют при непосредственном вычислении вероятностей.
Множества элементов, состоящие из одних и тех же элементов и отличающиеся друг от друга только их порядком, называют перестановками этих элементов. Число возможных перестановок из n элементов обозначают через Pn ; это число равно n! (читается энEфакториал):
Pn = n!, где n! =1 2 3 ... n.
По определению полагают 0!=1.
Размещениями называют множества, составленные из n различных элементов по m элементов, которые отличаются либо их составом, либо их порядком. Число всех возможных размещений определяется формулой
Anm = n(n −1)(n −2)...(n −m +1) .
Сочетаниями из n различных элементов по m называют множества, содержащие m элементов из числа заданных, и которые отличаются хотя бы одним элементом. Число сочетаний из n элементов по m выражается формулой
Cnm = |
n! |
|
. |
|
m!(n −m)! |
||||
|
|
|||
По определению полагают Cn0 =1.
Числа перестановок, размещений и сочетаний связаны равенством
Cnm = APnm m
Примеры
1.Сколькими различными способами могут разместиться на ска-
мейке 5 человек?
В соответствии с формулой Pn = n! получаем P5 =1 2 3 4 5 =120.
2.Сколькими способами можно избрать 3 лица на три одинаковые должности из десяти кандидатов?
Применяя формулу Cnm = |
|
|
n! |
|
, получаем |
|||||
m!(n −m)! |
||||||||||
|
|
|
|
|||||||
C3 |
= |
10! |
|
|
= |
10! |
= 10 9 8 =120 . |
|||
3!(10 −3)! |
|
|||||||||
10 |
|
3!7! |
|
1 2 3 |
||||||
|
|
|
||||||||
175
3. На пяти одинаковых карточках написаны буквы И, К, М, Н, С. Карточки перемешиваются и наугад раскладываются в ряд. Какова вероятность того, что получится слово МИНСК?
Из пяти различных элементов можно составить P5 перестановок: P5 = 1 2 3 4 5 = 120 . Значит, всего равновозможных исходов будет 120, и благоприятствующих данному событию – только одно. По
формуле классической вероятности получаем P ( A) = 1201 = 0,008, где событие А – появление слова МИНСК.
4. На отрезке натурального ряда от 1 до 20 найти частоту простых чисел.
На указанном отрезке находятся следующие простые числа: 2, 3, 5, 7, 11, 13, 17, 19; всего их 8. Так как n = 20 , m = 8 , то искомая частота
W= 208 = 0,4 .
5.При стрельбе по мишеням частота попаданий W = 0,75 . Найти
число попаданий при 40 выстрелах.
Из формулы W = mn следует, что m = Wn . Поскольку W = 0,75,
n = 40 , то m = 0,75 40 = 30 . Следовательно, было получено 30 попаданий.
6. Проведены три серии многократных подбрасываний монеты. Подсчитывалась частота появлений цифры (событие А), получены следующие результаты:
n |
m |
W (A) = m |
|
|
n |
4040 |
2048 |
0,5069 |
12000 |
6019 |
0,5016 |
24000 |
12012 |
0,5005 |
Приведенные данные свидетельствуют о том, что частота появления цифры на верхней стороне монеты (когда она упадет) при достаточно больших n незначительно отличается от вероятности появления цифры при однократном испытании
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P ( A)= 1 = 0,5, так как в этом случае m = 1, n = 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
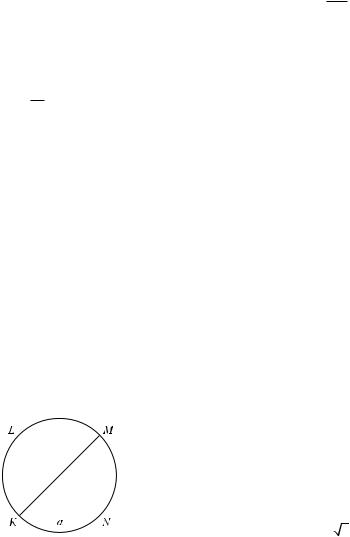
7. В круг вписан квадрат (рис. 13.5). В круг |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
наудачу брошена точка. Какова вероятность того, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
что точка попадет в квадрат? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Введем обозначения: событие А – попадание |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
точки в квадрат, R – радиус круга, а – сторона |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вписанного квадрата, причем a = 2R (так как |
|
|
|
|
Рис. 13.5 |
|
|
|
|
KM 2 = KN 2 + NM 2 , т.е. 2a2 = 4R2 , a2 = 2R2 ). Как |
||||||||||
176

известно, площадь круга S = πR2, а площадь квадрата выражается фор-
мулой S1 = 2R2. По формуле геометрической вероятности P ( A) = S S1
x2 + y2 =1 , а об49 16
ласть g – эллипсом |
x2 |
+ |
y2 |
=1 (рис. 13.6). В область G брошена точ- |
|||||
|
|
||||||||
25 |
|
|
9 |
|
|
|
|
|
|
ка. Найти вероятность того, что точка попадет в область g? |
|||||||||
Как известно, площадь эллипса |
x2 |
+ |
y2 |
=1 равна S = πab. В данном |
|||||
a2 |
|
||||||||
|
|
|
|
|
|
|
b2 |
||
случае SG = π 7 4 = 28π, |
Sg = π 5 3 =15π . Следовательно, P ( A) = |
||||||||
=1528ππ = 1528 = 0,536 .
9.Подбрасывается два игральных кубика. Найти вероятность события А – «сумма выпавших очков не превосходит четырех».
Событие А есть сумма трех несовместных событий B2, B3, B4 и заключается в том, что сумма очков равна соответственно 2, 3, 4. Пос-
кольку P (B2 ) = 361 , P (B3 ) = 362 , P (B4 ) = 363 , то по теореме сложения вероятностей несовместных событий получим:
P ( A) = P (B2 ) +P (B3 ) +P (B4 ) = 361 + 362 + 363 = 366 = 61 .
З а м е ч а н и е. Тот же результат можно получить непосредственно. Действительно, событию А благоприятствуют 6 элементарных исходов: (1,1), (1, 2), (2, 1), (1,3), (3,1), (2, 2). Всего элементарных исходов, образующих полную группу событий, n = 36, поэтому
P ( A) = 366 = 61 .
10. Вероятность попадания при стрельбе по мишени для первого спортсмена рана 0,85, для второго – 0,8. Спортсмены независимо друг
от друга сделали по одному выстрелу. Найти |
|
вероятность того, что в мишень попадет хотя |
|
бы один спортсмен. |
|
Введем обозначения событий: А – «по- |
|
падание первого спортсмена», В – «попада- |
|
ние второго спортсмена», С – «попадание |
|
хотя бы одного из спортсменов». Очевидно, |
|
A +B =C , причем события А и В совмест- |
Рис. 13.6 |
177

ны, но независимы. По теореме сложения вероятностей Ρ( A + B) = = P ( A) + P (B) − P ( AB) в данном случае находим:
P (C ) = (0,85 +0,8) −0,85 0,8 = 0,97 .
11. Симметричная монета подброшена три раза. Какова вероятность того, что «цифра» появится два раза.
Введем обозначения: Аk – «выпадение цифры при kEтом подбра-
сывании (k = 1, 2, 3), Ak – соответствующие противоположные события», А – «выпадение двух цифр при трех подбрасываниях», тогда
A = A1A2A3 + A1A2A3 + A1A2A3 . Поскольку слагаемые в правой части попарно несовместны, то по теореме сложения вероятностей несовместных событий
P ( A) = P (A1A2A3 ) + P (A1A2A3 ) + P (A1A2A3 ).
Принимая во внимание независимость событий A1, A2, A3 , находим искомую вероятность
P ( A) = P ( A1 )P ( A2 )P (A3 ) + P ( A1 )P (A2 )P ( A3 ) + P (A1 )P ( A2 )P ( A3 ) =
=12 12 12 + 12 12 12 + 12 12 12 = 83 = 0,375.
12.В урне находятся 8 красных и 6 голубых шаров. Из урны последовательно без возвращения извлекаются 3 шара. Найти вероятность того, что все 3 шара голубые.
Введем обозначения событий: A1 |
– «первый шар голубой», A2 – |
|||||||||||||||||||||||
«второй шар голубой», A3 |
– «третий шар голубой», А – «все три ша- |
|||||||||||||||||||||||
ра голубые», тогда A = A1A2A3 . По теореме умножения вероятностей |
||||||||||||||||||||||||
P ( A A A ) = P |
( A ) |
P ( A / A ) P ( A / A A ) . Поскольку |
P ( A ) = |
6 |
, |
|||||||||||||||||||
|
||||||||||||||||||||||||
1 |
2 |
3 |
|
|
|
1 |
|
2 |
1 |
|
|
|
|
3 |
1 |
2 |
1 |
14 |
|
|||||
|
|
|
|
5 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
||
P ( A |
/ |
A ) = |
|
, P |
( A |
/ A A ) = |
|
, то |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2 |
|
1 |
13 |
|
3 |
1 |
2 |
12 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
P ( A) = |
|
6 |
|
5 |
|
4 |
= |
|
5 |
= 0,055. |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
14 13 12 |
91 |
|
|
|
|
||||||||||
З а м е ч а н и е. Эту вероятность |
можно найти |
|||||||||
P ( A) = m |
. Поскольку в данном случае |
|
|
|||||||
n |
|
|
|
|
|
|
|
|
|
|
|
n =C3 |
= |
14! |
, m =C3 |
= |
|
6! |
|
, P ( A) = |
C63 |
|
14 |
3!11! |
6 |
|
3!3! |
C143 |
||||
|
|
|
|
|||||||
ипо формуле
,то
P ( A) = |
6! |
: |
14! |
|
= 6! 3! 11! |
= 6! 11! |
= |
|
4 5 6 |
= |
5 |
= 0,055. |
|
3!3! |
3!11! |
12 13 14 |
91 |
||||||||||
|
|
14! 3! 3! |
14! 3! |
|
|
|
|||||||
178

13. В каждом из трех ящиков находится по 30 деталей. В первом ящике 27, во втором 28, в третьем 25 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Какова вероятность того, что все три извлеченные детали окажутся стандартными.
Вероятность того что из первого ящика вынута стандартная деталь (событие А) P ( A) = 2730 = 109 . Вероятность того, что из второго ящика вынута стандартная деталь (событие В) P (B) = 2830 = 1415 . Вероятность того, что из третьего ящика вынута стандартная деталь (событие С)
P (C ) = 25 |
= 5 . По теореме умножения независимых событий А, В, С |
||||
30 |
6 |
|
|
||
P ( ABC ) = |
|
9 |
14 |
5 |
= 0,7. |
|
|
||||
|
10 15 |
6 |
|
||
14. На распределительной базе находятся электрические лампочки, изготовленные на двух заводах. Среди них 60 % изготовлено на первом заводе и 40 % – на втором. Известно, что из каждых 100 лампочек, изготовленных первым заводом, 95 является стандартными, а из 100 лампочек, изготовленных вторым заводом, 85 удовлетворяют стандартам. Определить вероятность того, что взятая наугад лампочка будет стандартной.
Обозначим через А событие, состоящее в том, что взятая лампочка является стандартной. Введем две гипотезы: H1 – «лампочка изготовлена первым заводом», H2 – «лампочка изготовлена вторым заводом». Из условия задачи следует, что P (H1 ) = 0,6, P (H2 ) = 0,4; P ( A / H1 ) = 0,95, P ( A / H2 ) = 0,85 . По формуле полной вероятности при n = 2 P ( A) = P (H1 )P ( A / H1 ) + P (H2 )P ( A / H2 ) получаем
P( A) = 0,6 0,95 + 0,4 0,85 = 0,57 + 0,34 = 0,91.
15.На фабрике машины a, b, c производят соответственно 20 %, 35 %, 45 % всех изделий. В их продукции брак составляет 3 %, 2 %, 4 %. Какова вероятность того, что случайно выбранное дефектное изделие произведено машинами a, b, c соответственно.
Пусть событие А состоит в том, что случайно выбранное изделие
является дефектным, а H1, H2, H3 – события, состоящие в том что изделие произведено машинами a, b, c соответственно.
События H1, H2, H3 образую полную группу событий. Числа 0,20, 0,35, 0,45 (20 %, 35 %, 45 %) являются вероятностями этих событий, т.е. P (H1 ) = 0,20 , P (H2 ) = 0,35, P (H3 ) = 0,45. Аналогично, числа 0,03, 0,02, 0,04 (3 %, 2 %, 4 %) будут условными вероятностями события А
179
