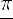Билеты экзамен
.pdf
Вопрос 1.41
Двугранный угол — пересечение двух полупространств, образованных непараллельными плоскостями
Линейный угол двугранного угла — пересечение данного двугранного угла и плоскости, перпендикулярной его ребру
Угол между плоскостями — наименьший из двугранных углов, образованных при пересечении данных пересекающихся плоскостей
Вопрос 1.42
Две плоскости называются взаимно перпендикулярны, если они образуют прямые двугранные углы.
Признак перпендикулярности плоскостей. Если одна из двух плоскостей проходит через прямую перпендикулярно другой плоскости, то эти плоскости перпендикулярны.
Свойства перпендикулярных плоскостей:
1.Если прямая лежит в одной из двух взаимно перпендикулярных плоскостей и перпендикулярна линии их пересечения, то эта прямая перпендикулярна другой плоскости.
2.Если прямая, проведенная через точку одной из двух взаимно перпендикулярных плоскостей, перпендикулярна другой плоскости, то она лежит в первой из них.
3.Если две плоскости, перпендикулярные третьей плоскости, пересекаются, то прямая их пересечения перпендикулярна третьей плоскости.
Вопрос 1.43
Степень с целым показателем: 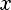
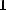

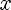
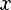
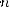

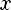
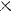
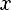
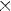
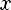
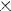
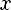 (n раз)
(n раз)
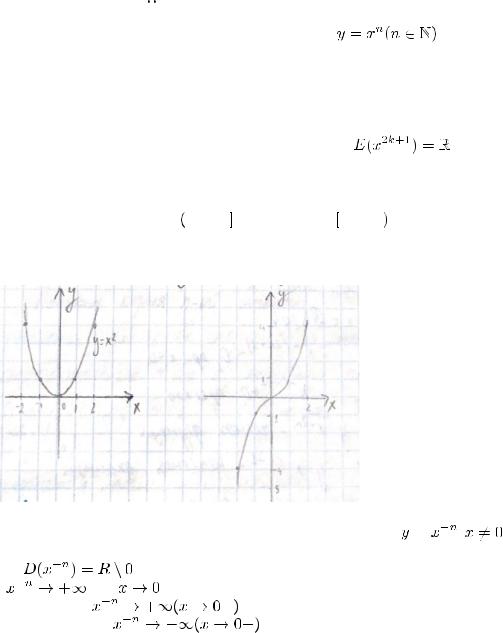
Степенная функция с натуральным показателем
1.Вариант: n — чётная (n = 2k)
2.Вариант n — нечётная (n = 2k + 1)
Свойства 1) 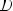






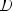








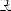
2) Вертикальных асимптот нет 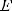










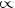

3) 


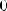




4)при n = 2k — чётная, при n = 2k + 1 - нечётная
5)y = x^n — непериодическая
6)при n = 2k убывает на 
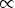

 , возрастает на
, возрастает на 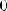


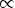
при нn = 2k + 1 возрастает на 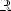
7) при n = 2k функция ограничена снизу (нулём), но не ограничена сверху при n = 2k + 1 функция неограничена ни сверху, ни снизу
Степенная функция с целым отрицательным показателем |
, |
|
Свойства |
|
|
1) |
(0 — вертикальная асимптота) |
|
при |
|
|
при n = 2k |
|
|
при n = 2k + 1 |
|
|
2)при n = 2k 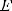











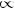
 при n = 2k + 1
при n = 2k + 1 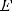









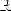
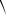

3)


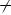

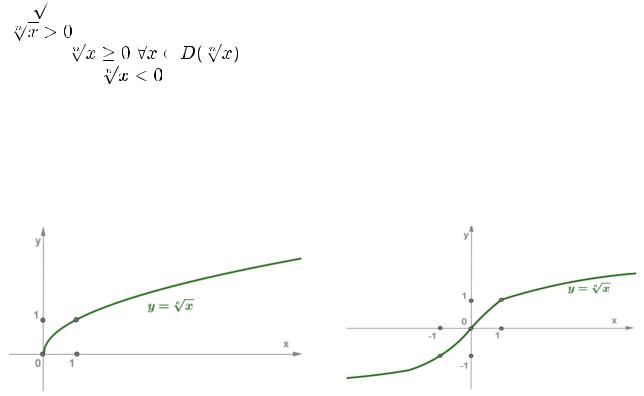
Вопрос 1.44
Понятие корня n-ой степени
1)для n = 2k корнем n-ой степени из неотрицательного числа a называется такое неотрицательное число b (обозначается 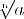 , то
, то 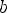


 )
)
2)корнем нечётной степени из числа a называется такое число b (обозначается
 ), n-ая степень которого равно a
), n-ая степень которого равно a
Арифметическим корнем n–й степени из неотрицательного числа a называется неотрицательное число, n–я степень которого равна a.
Алгебраическим корнем n–й степени из данного числа называется множество всех корней из этого числа. Алгебраический корень чётной степени имеет два значения: положительное и отрицательное.
Функция 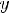

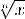
Свойства
1)при n = 2k 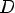

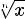






 при n = 2k + 1
при n = 2k + 1 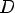

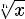


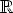
2)при n=2k 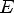

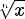






 при n=2k + 1
при n=2k + 1 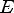

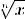


3)
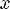

 при x=0
при x=0
при x > 0
n = 2k: |
|
n = 2k + 1^ |
при x < 0 |
4)n = 2k: общего вида n = 2k + 1: нечётная
5)непериодическая
6)монотонно возрастает на всей области определения
7)n = 2k: ограничена снизу нулем, сверху неограничена n = 2k+1: не ограничена ни сверху, ни снизу

Вопрос 1.45
Степень положительного числа с рациональным показателем
Пусть a > 0, а p/q — рациональное число (q >=2), по определению число a в степени p/q есть арифметический корень степени q из a в степени p
Свойства
Пусть a и b— положительные числа, r, r1 и r2 — рациональные числа, тогда:
1) 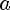


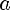



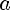


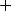

 2)
2) 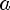


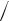
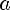



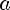




 3)
3) 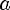





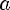




 4)
4) 
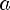
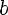



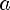

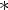
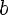

5) 
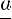



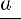
Степенью положительного числа a с иррациональным показателем α
называют выражение a^α, значение которого равно пределу последовательности a^α0, a^α1… , где α0, α1, α2...- последовательные десятичные приближения иррационального числа α.
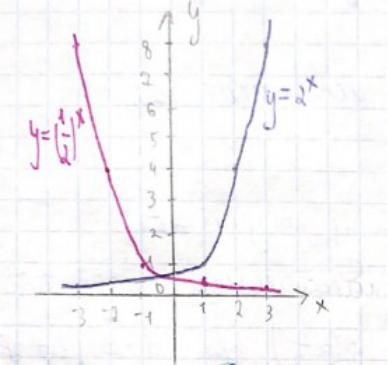
Вопрос 1.46
Показательная функция — функция вида 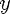

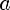
 , где a>0, a
, где a>0, a 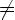 1
1
Свойства
1) 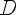

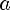



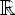 2)
2) 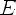

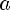






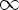
 3)
3) 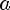

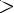

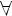
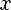

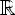
4)общего вида
5)непериодическая
6)при a > 1 — монотонно возрастает, при 0<a<1 монотонно убывает
7)ограничена снизу нулем, сверху не ограничена
8)общая точка всех показателей — (0;1)
9)задает одно-однозначное соответствие
Вопрос 1.47
Функция 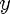

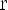
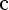

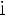
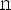
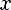
1)D(f) = -1 <= x <= 1
2)E(f) = 
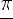

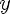

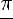
3)монотонно возрастает
4)максимумы: x = 1, y = 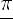
5)минимумы: x = -1, y = 

6)y = 0 при x = 0
7)x = 0 при y = 0
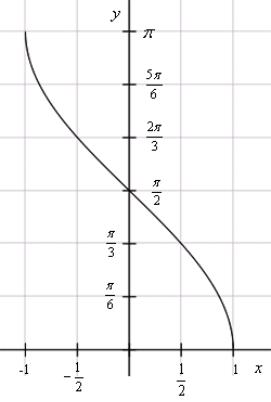
Вопрос 1.48
Функция 

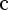
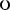

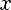
Свойства:
1)D(f) = -1 <= x <= 1
2)E(f) 
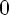

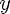
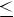

3)монотонно убывает
4)максимумы: x = -1, y = 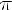
5)минимумы: x = 1, y = 0
6)y = 0 при x = 1
7)x = 0 при y = 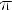
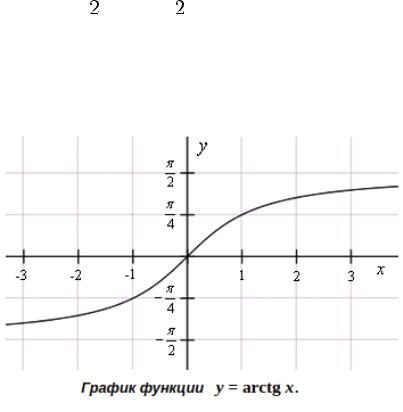
Вопрос 1.49
Функция 

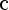
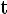
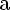

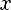
Свойства:
1) 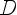

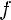


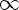
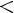
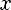
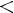
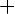
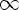 2)
2) 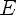

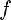
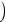


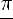
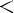
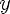
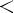

3)монотонно возрастает
4)максимумов минимумов нет
5)y = 0 при x = 0
6)x = 0 при y = 0
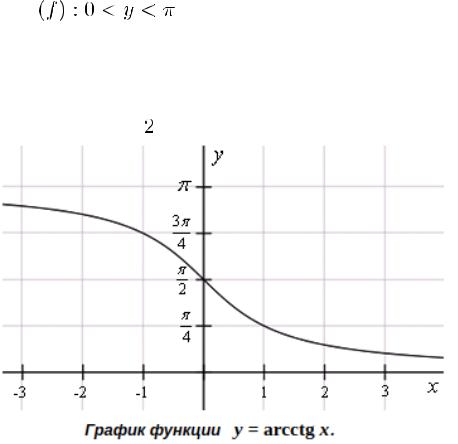
Вопрос 1.50
Функция y = arcctg x
Свойства:
1) 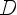

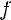
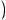


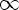
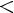
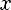
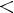


2) 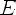
3)монотонно убывает
4)максимумов минимумов нет
5)нулей нет
6)x = 0 при y =