Билеты экзамен

Вопрос 1.31

Формула дополнительного аргумента

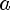
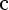
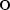
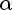
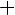
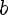
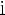
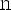
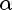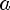
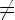
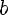
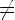
Рассмотрим выражение , при условии или Тогда это выражение можно разделить на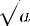

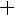
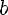
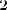
Введём вспомогательный аргумент и такой, что ;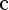

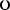
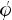
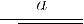Такой угол существует, тк 1)

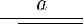
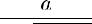
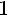
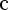
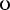
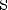
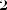
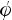
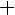
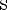
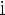
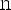
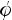
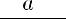
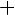
2) 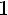Тогда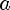

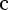
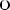
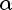
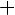
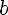
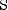
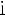
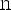
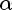
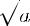
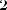
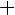
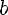
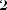
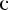
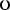
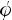
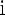
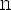
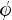
Если взять наоборот ; 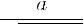, то получим

Аналогично выводятся формулы

Вопрос 1.32

Алгебраическое выражение вида Pn(x) = anxn + an-1xx-1 + ….. + a1x + a0 называют многочленом степени n при

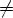
Степенью многочлена называется наибольший показатель степени этого многочлена. Член, содержащий эту степень, называется старшим.

Сложение и вычитание многочленов. При сложении (вычитании) многочленов происходит сложение (вычитание) коэффициентов при равных степенях многочленов. (приведение подобных членов). При сложении(вычитании) многочленов разных степеней получается многочлен большей степени. При сложении(вычитании) многочленов одинаковой степени получается многочлен степени, не превышающей степени исходных многочленов.

Умножение многочленов. Чтобы умножать многочлен Pn(x) на многочлен Rm(x) нужно каждый одночлен первого многочлена умножить на каждый одночлен другого многочлена(раскрыть скобки). Полученные произведения сложить(привести подобные слагаемые).

Корень многочлена. Число 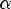называется корнем многочлена Pn(x), если Pn(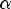) = 0

Вопрос 1.33

Деление на многочлен с остатком

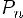
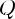
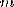
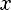
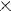
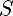
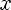
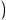
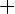
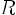
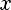
Разделить многочлен Pn(x) на многочлен Qm(x) с остатком означает представить Pn(x) в виде 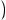, где степень многочлена R(x) < m (меньше степени делителя)

При этом Pn(x) — делимое, Qm(x) — делитель, Sn-m(x) — частное, R(x) — остаток

Теорема Безу

Остаток от деления многочлена Pn(x) на линейный двухчлен (x-a) равен значению многочлена в точке a (Pn(a))

Следствие 1

Если a — корень многочлена, то Pn(x) делится нацело на (x-a)

Следствие 2

Если a1 и a2 — два различных корня многочлена, то этот многочлен делится нацело на квадратный трехчлен (x-a1)*(x-a2) = x^2 — (a1+a2)x + a1*a2

Вопрос 1.34

Кратность корня многочлена. Число 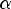называется корнем иного члена Pn(x) кратности K, если Pn(x) кратно (x - 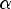)k, но Pn(x) не кратно (x - 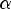)k+1

Теорема о целых корнях многочлена с целыми коэффициентами. Целые корни многочлена с целыми коэффициентами являются делителями свободного члена.

Теорема о рациональных корнях многочлена с целыми коэффициентами.

Пусть рациональный корень многочлена Pn(x) = anxn + an-1xx-1 + ….. + a1x + a0. С целыми коэффициентами представлен в виде несократимой дроби P/q

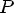
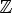
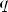
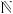
. Тогда числитель дроби является делителем свободного члена, а знаменатель — делителем коэффициента при старшей степени. (a0 кратно p; an кратно q)

Вопрос 1.35

Дробно-рациональная функция — функция, представляющая собой алгебраическую дробь, у которой числитель и знаменатель — многочлены некоторой степени

Правильная дробь — дробь, у которой степень многочлена в числителе меньше степени многочлена в знаменателе

Простейшая дробь — правильная рациональная дробь, у которой знаменатель является степенью неприводимого многочлена (не имеет общих делителей с числителем)

Теорема

Всякая рациональная дробь представима, при том единственным образом, в виде суммы многочлена и правильной дроби

Теорема

Если 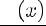- правильная несократимая рациональная дробь, а её

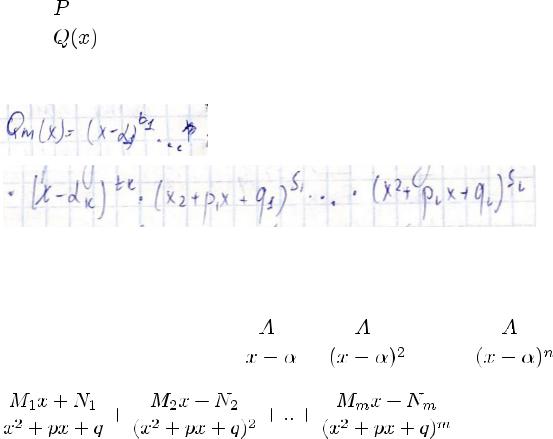
знаменатель после разложения на неприводимые многочлены имеет вид

то рассматриваемая дробь может быть представлена, притом единственным образом, в виде суммы простейших рациональных дробей, причём каждой степени n линейного множителя (x-a)n

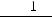
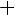
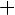
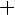
соответствует разложение 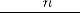, а каждой степени квадратного трёхчлена соответствует разложение

Вопрос 1.36

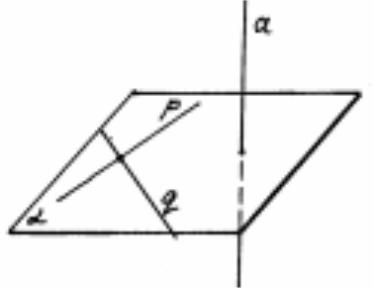
Понятие угла между параллельными, пересекающимися и скрещивающимися прямыми.

1.Угол между параллельными прямыми — 0 градусов

2.Угол между пересекающимися прямыми — меньший из двух углов

3.Угол между скрещивающимися прямыми — меньший угол между двумя пересекающимися прямыми, которые соответственно параллельны заданным скрещивающимся прямым

Вопрос 1.37

Прямая называется перпендикулярной к плоскости, если она перпендикулярная к любой прямой, лежащей в этой плоскости.

Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к этой плоскости.

Вопрос 1.38

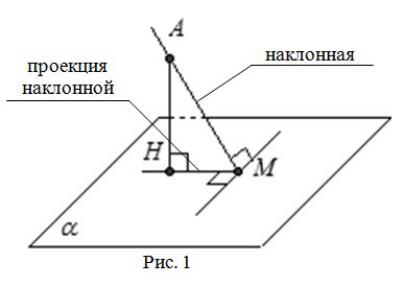
Теорема о 3-х перпендикулярах. Если прямая, лежащая на плоскости, перпендикулярна проекции наклонной на эту плоскость , то данная прямая перпендикулярна и самой наклонной.

Обратная теорема о 3-х перпендикулярах. Если на плоскости проведена прямая перпендикулярно наклонной, то эта прямая перпендикулярна проекции наклонной.

Вопрос 1.39

Расстоянием между двумя фигурами называется расстояние между ближайшими точками этих фигур (если такие точки есть). Расстояние от точки до фигуры является частным случаем расстояния между фигурами, когда одна фигура — точка. Расстояние между фигурами будем обозначать | F1F2 |, где F1 и F2 — данные фигуры.

Расстояние между скрещивающимися прямыми — это расстояние между одной из этих прямых и плоскостью, проходящей через вторую прямую параллельно первой.

Вопрос 1.40

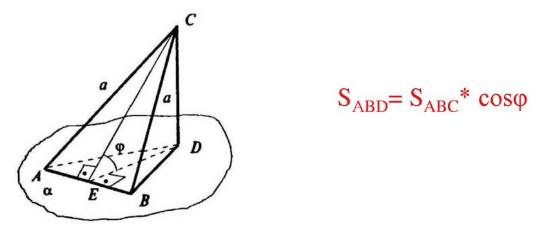
Теорема о площади ортогональной проекции многоугольника.

Площадь ортогональной проекции многоугольника на плоскость равна площади проецируемого многоугольника, умноженной на косинус угла между плоскостью многоугольника и плоскостью проекций.