
Билеты экзамен
.pdf
Вопрос 1.21
Определение функций |
и тд |
1)Числу 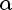 становится в соответствие точка P
становится в соответствие точка P тригонометрической окружности
тригонометрической окружности
2)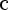
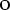
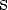
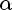 = x*P
= x*P = проекция ox P
= проекция ox P

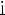
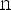
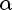 = y *P
= y *P = проекция oy P
= проекция oy P
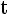
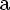
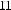
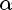 = y *P
= y *P / x * P
/ x * P = y/x
= y/x 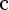

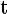
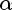 = x * P
= x * P y *P
y *P = x/y
= x/y
Число b, равное ординате единичного радиуса, построенного описанным способом, обозначается 
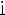
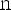
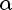 и называется синусом угла α.
и называется синусом угла α.
Число a, равное абсциссе конца единичного радиуса, построенного описанным способом, обозначается 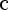
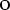
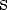
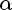 и называется косинусом угла α.
и называется косинусом угла α.
Функция tgx=sinx/cosx при x≠π/2+πk, kЄZ, называется котангенсом угла x. Область определения функции tgx это все действительные числа, кроме x=π/2+πn, nЄZ.
Функция ctgx=cosx/sinx при x≠πk, kЄZ называется котангенсом угла x. Область определения функции ctgx = -все действительные числа кроме точек x=πk, kЄZ.
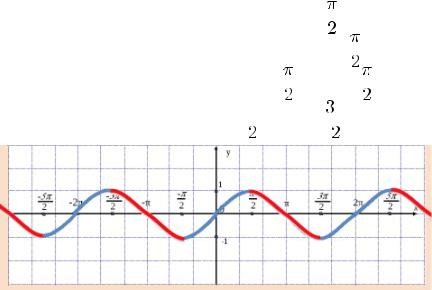
Вопрос 1.22
Свойства функции y = sin x:
1.Область определения - R
2.Область значений - [-1; 1]
3.Функция переодическая с периодом 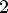
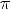
4.Функция нечётная
5.y = 0 при 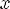

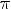
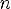 ,
, 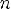

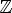
6.y > 0 при 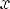



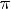
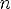

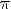


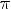



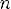
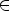

y < 0 при 


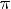

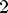
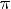
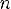


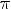

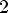
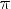
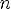




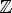
7.Наибольшее значение y = 1 при 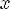



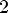
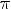
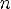

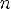

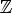 Наименьшее значение y = -1 при
Наименьшее значение y = -1 при 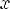




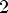
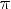
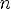

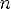

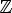
8.Функция возрастает при 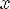






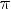
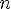




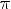
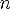


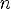

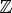 Функция убывает при
Функция убывает при 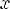


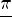


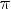
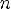

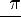

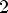
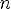



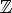
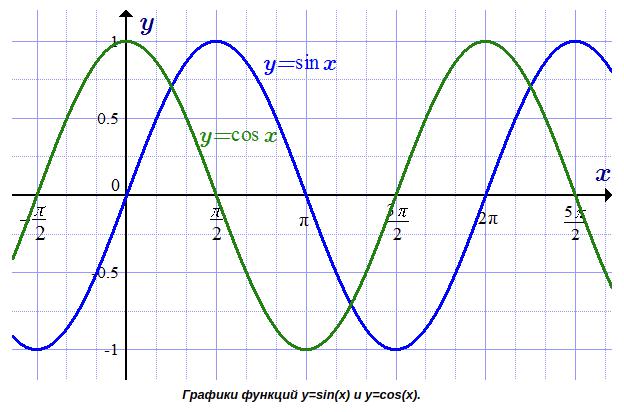
Вопрос 1.23
Свойства косинуса
D(f) = 
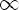
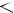
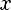
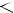
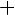
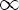 E(f) = -1 <= y <= 1
E(f) = -1 <= y <= 1
Возрастание -π + 2πn <= x <= 2πn Убывание 2πn <= x <= π + 2πn Макс; мин: x=2πn; x = π + 2πn Нули: x = π/2 + πn
Чётная Период = 2π
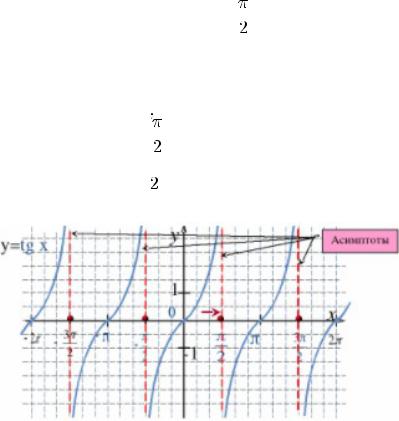
Вопрос 1.24
Свойства функции y = tg x:
1.Область определения - 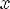
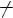


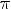
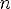

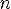

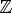
2.Область значений — R
3.Функция переодическая с периодом 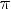
4.Функция нечетная
5.y = 0 при 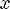

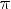
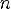
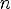

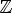
6.y > 0 при 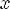





 и при сдвиге на
и при сдвиге на 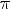
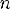

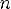

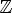 y < 0 при
y < 0 при 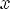



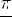


 и при сдвиге на
и при сдвиге на 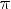
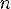

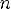

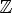
7.Возрастает на всей области определения
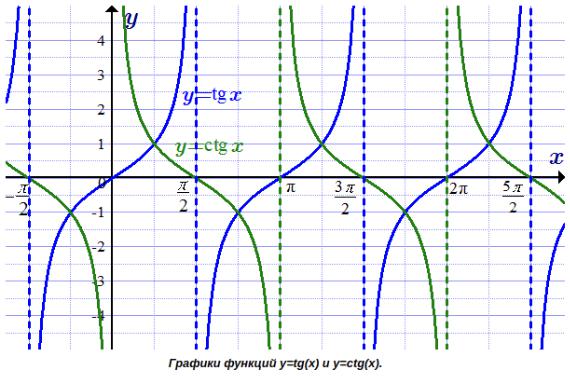
Вопрос 1.25
Свойства котангенса
D(f) = 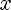
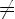
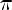
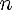
E(f) = 
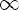

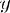
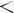
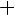
 Возрастание - Убывание πn < x < π + πn Макс; мин: -
Возрастание - Убывание πn < x < π + πn Макс; мин: -
Нули: x = π/2 + πn
Нечётная Период = π
Вопрос 1.26
Основное тригонометрическое тождество: 
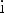








Формулы сложения:

Вопрос 1.27
Формулы приведения

Вопрос 1.28
Формулы двойного угла: |
Формулы половинного аргумента: |
Формулы понижения степени: |
Универсальная тригонометрическая |
|
подстановка: |
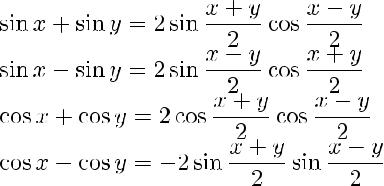
Вопрос 1.29
Формулы преобразования суммы (разности) тригонометрических функций в произведение
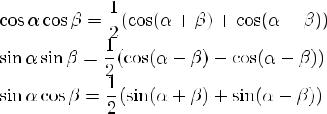
Вопрос 1.30
Формулы преобразования тригонометрических функций в сумму или разность:
