Билеты экзамен

Вопрос 1.1

Пересечение множеств – это их общая часть, то есть множество C всех элементов, которые принадлежат как множеству A, так и множеству B.

Объединение множеств – множество C, состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств (или A или B)

Разность множеств – множество C, которое состоит из всех элементов, принадлежащих A и не принадлежащих B

Дополнением множества A называется множество элементов, состоящее из всех элементов, не принадлежащих множеству A, но принадлежащих универсальному множеству.

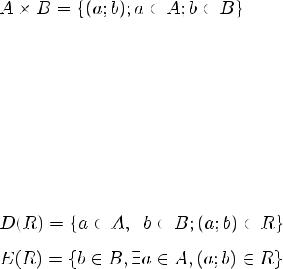
Вопрос 1.2

Упорядоченной парой называется объект (a;b), который состоит из двух элементов и в котором определенно какой из элементов считать первым (первой компонентой / координатой), а какой вторым (второй компонентой / координатой)

Декартовое произведение двух множеств A и B называется множество A x B, элементами которого являются всевозможные упорядоченные пары (a;b), 1-е компоненты которого принадлежат A, а 2-е компоненты принадлежат B.

Соответствием R между A и B называют любое подмножество декартового произведения AxB.

Область определения соответствующая R называется любое подмножество 1-х компонентных пар, принадлежащих R, а множество области значения называется множеством 2-х компонентных пар, т. е.

Вопрос 1.3

Соответствием R между A и B называют любое подмножество декартового произведения AxB

Область определения соответствующая R называется множеством 1-х компонентных пар, принадлежащих R, а множество области значения называется множество 2-х компонентных пар, то есть:

Способы задания соответствий:

1)перечисление

2)характерист. Свойствами

Виды соответствий:

1)Одно-однозначное – у каждого элемента из области определения единственный образ, и у каждого из области значений единственный прообраз

2)Много-однозначное – у каждого элемента из области определения единственный образ, но для некоторых элементов из области значений несколько прообразов

3)Одно-многозначное – у каждого элемента из области значений единственный прообраз, но существует хотя бы один x, у которого хотя бы 2 образа

4)Много-многозначное – у хотя бы одного элемента из области определения есть хотя бы 2 образа, и у хотя бы одного элемента из области значений есть хотя бы 2 прообраза

Виды соответствий 2:

1)Для любого x из области определения 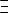! Y из области значения R, yRx.

2)Для любого y из области значения ! X из области определения R, xRy.

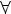
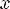
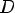
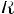
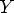
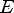
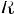
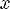
Соответсвие R называется много-однозначным(M-I), если: 1. 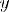2.

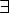
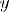
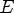
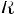
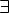
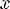
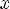
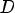
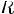
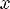
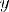
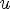
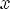
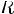
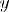
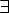
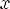
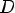
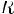
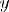
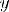
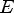
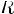
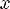
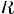
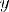
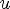
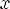
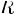
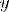
Соответствие R называется одно-многозначным(I-M), если: 1. 2.

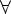
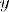
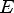
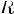
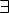
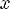
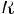
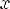
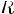
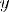
Соответствие R называется много-многозначным(M-M), если: 1.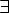

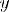
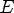
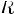
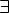
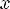
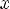
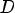
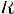
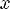
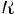
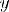
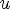
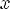
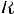
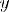
2.

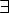
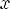
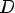
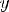
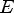
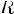
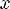
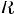
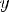
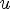
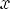
Вопрос 1.4

Соответствием R между A и B называют любое подмножество декартового произведения AxB.

Соответствием между множествами x и y называется

функциональным (функцией) если оно одно-однозначное или многооднозначное.

X - множество первых элементов упорядоченных пар, называемо

областью определения функции.

Y - множество вторых элементов упорядоченных пар, называемо

областью значения функции.

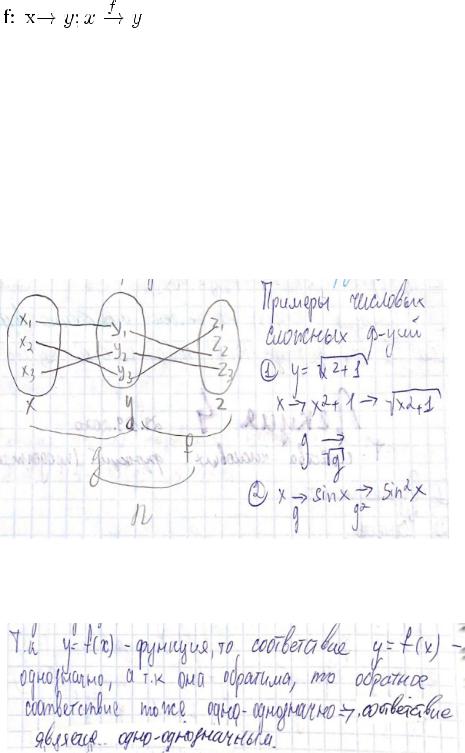
Вопрос 1.5

Функциональное соответствие — соответствие между множествами x и y, если оно одно-однозначно или много-однозначно

Обратная функция: если соответствие y = f(x) является функцией, и обратная к нему y = f-1(x) так же является функцией, то y = f-1(x) называется функцией, обратной к y = f(x)

Сложная функция:

Пусть функция f: y → z, a функция g: x → y Причем E(g) является подмножеством D(f) E(g) <= D(f)

Тогда существует функция n(x) = f(g(x)

n: x → z — называемая сложной функцией

Критерии обратимости функции:

1) Функция y = f(x) обратима <=> когда y = f(x) одно-однозначное соответствие Док-во:

м

2) Если соответствие y = f(x) — одно-однозначное, что обратное ему соответствие тоже одно-однозначное => оно является функцией => y = f(x) — обратимая чтд

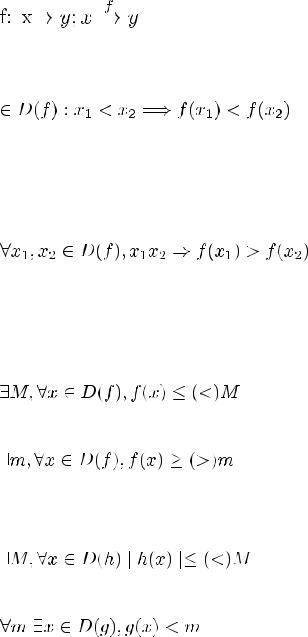
Вопрос 1.6

Функциональное соответствие — соответствие между множествами x и y, если оно одно-однозначно или много-однозначно

Функция y = f(x) называется монотонно возрастающей, если для (x1;x2) – любая пара чисел,

Функция y = g(x) не является монотонно возрастающей если 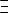(x1;x2) из D(f), такая что x1 < x2, но f(x1) > f(x2)

Функция y = f(x) называется монотонно убывающей, если

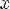
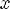
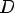
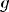
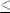Функция y = g(x) не является монотонно убывающей, если , x1 < x2, но f(x1) f(x2)

Функция y = h(x) называется ограниченной сверху, если

Функция y = h(x) называется ограниченной снизу, если

Функция y = h(x) называется ограниченной, если она и сверху и снизу ограничена.

Функция y – f(x) называется неограниченной снизу, если

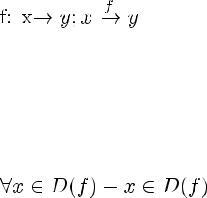
Вопрос 1.7

Функциональное соответствие — соответствие между множествами x и y, если оно одно-однозначно или много-однозначно

Функция y = f(x) называется чётной, если

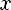
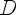
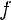
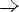
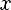
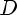
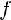
, то есть D(f) симметрична относительно Oy f(-x) = f(x)

Функция называется нечётной, если

, то есть симметрична относительно точки O

g(-x) = -g(x)

Если функция не является ни чётной, ни нечётной, то она называется функцией общего вида

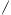
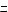
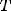
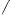
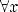
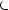
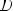
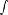
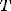
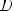
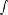
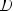
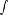
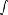
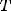
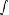
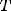
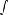
Периодическая функция — функция y = f(x) называется периодической, если существует число T выполняется Число T в этом случае называется периодом функции, а наименьшее положительное из этих T называется основным периодом функции

Вопрос 1.8

Если соответствие y = f(x) является функцией, и обратное к нему

y = f -1(x) также является функцией, то y = f -1(x), называется функцией обратной к y = f(x)

Достаточное условие обратимости функции - функция обратима тогда и только тогда, когда она является строго монотонной, то есть строго возрастает или строго убывает на всём своём промежутке.

Свойства графиков взаимно обратных функций:

1.D(f) совпадает с областью значений E(g) D(f) = E(g)

2.E(f) = D(g)

3.f(g(x)) = x 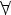x D(g)

4.g(f(x)) = x 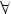x D(f)

Вопрос 1.9

Функция y = f(x) называется чётной, если

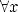
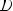
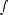
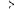
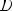
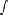
, то есть D(f) симметрична относительно Oy f(-x) = f(x)

Функция называется нечётной, если

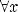
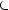
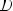
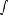
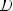
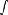
, то есть симметрична относительно точки O g(-x) = -g(x)

Теоремы о графиках чётных и нечётных функций:

1)график чётной функции симметричен относительно оси Oy

2)график нечётной функции симметричен относительно начала координат (точки (0;0))

Арифметические теоремы о чётных и нечётных функций

1)сумма (разность) двух чётных функций является чётной на пересечении D(f) и D(g)

2)сумма (разность) двух нечётных функций является нечётной функцией

3)произведение (частное) двух чётных функций является чётной

4)произведение (частное) двух нечётных функций является чётной

5)произведение (частное) чётной и нечётной функций является чётной

Вопрос 1.10

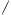
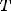
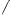
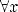
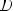
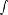
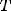
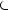
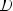
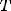
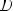
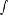
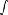
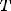
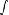
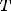
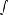
Периодическая функция — функция y = f(x) называется периодической, если существует число T выполняется Число T в этом случае называется периодом функции, а наименьшее положительное из этих T называется основным периодом функции

Теоремы о периодических функциях:

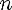
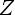
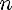
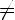
Теорема 1. Если T0 - основной период функции y = f(x), то все числа вида nT0 и только они являются периодами функции y = f(x)

Теорема 2. О периоде функции y = f(kx), если T – период функции y=f(kx) (при k 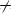0), будет число