Добавил:

Dolin_TOP Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский технический университет связи и информатики

Предмет:

Высшая математика

Файл:

Вышмат

.pdf

Скачиваний:

Добавлен:

04.12.2024

Размер:

950.34 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1110 11 > Следующая >>>

Вариант 25

В примерах с 1 по 14 решить задачи в соответствии с условиями варианта задания:

в примерах 1- 9, 11 найти общее решение (общий интеграл) или частное решение дифференциального уравнения;

в примере 10 написать общее решение дифференциального уравнения

со специальной правой частью, не находя числовых значений неопределенных коэффициентов частного решения;

в примере 12 решить дифференциальное уравнение с помощью формулы Тейлора (найти первые три ненулевых члена разложения по формуле Тейлора);

в примерах 13-14 решить геометрическую и физическую задачу, путем составления дифференциального уравнения.

25.1xy2 x dx x2 y y dy 0; y 0 1.

25.2x y 2 dx x y 4 dy 0.

25.3y 2xy xe x2 .

25.4xdx ydy xdyx2 yydx2 .

25.5y xex ; y 0 0,y 0 0.

25.6yy y 3 .

25.7 y 1 lny y 1 lny y 2 0; y 0 y 0 1.

25.8y 2y 9y 18y 0; y 0 1,y 0 3,y 0 9.

25.9y 2y 5y e xsin2x.

25.10y 2y 5y 4xe-x -68cos2x x.

25.11y y e2ex2x 1.

25.12 y 2xy2 e3x ;

y 0 1.

25.13Записать уравнения кривых, для которых длина отрезка, отсекаемого нормалью в точке M x; y на оси Ox , равна y2 / x .

25.14Изолированному проводнику сообщен заряд q0 1000 CGSE единиц.

Вследствие несовершенства изоляции проводник постепенно теряет свой заряд. Скорость потери заряда в данный момент пропорциональна наличному заряду проводника. Какой заряд останется на проводнике по истечении времени t 10 мин, если за первую минуту потеряно 100 CGSE единиц?

Вариант 26

В примерах с 1 по 14 решить задачи в соответствии с условиями варианта задания:

в примерах 1- 9, 11 найти общее решение (общий интеграл) или частное решение дифференциального уравнения;

в примере 10 написать общее решение дифференциального уравнения

со специальной правой частью, не находя числовых значений неопределенных коэффициентов частного решения;

в примерах 13-14 решить геометрическую и физическую задачу, путем составления дифференциального уравнения.

26.1 tgxsin2 ydx cos2xctgydy 0.

26.2xy y xe x .

26.3y 1 x22x y 1.

26.43x2 1 lny dx x3 2y dy.

26.5x4 y x3 y 1; y(1) 0,y (1) 0 .

26.6y tgx y 1.

26.7	y			2			0 2.
26.7	y		1 y y		y ;	y 0 y	0 2.

26.8y V 6y IV 9y 0; y 0 y 0 y 0 y 0 0,y IV 0 27.

26.9y y x2.

26.10y 4y 24e2x 4cos2x 8sin2x.

26.11y y ctgx.

26.12y 4 xy y x2; y 0 y 0 y 0 y 0 1.

26.13Записать уравнения кривых, для которых длина отрезка, отсекаемого нормалью в точке M x; y на оси Oy , равна x2 / y .

26.14Пуля входит в брус толщиной 12 см со скоростью 200 м/с, а вылетает из него, пробив его, со скоростью 60 м/с. Брус задерживает движение пули, сила сопротивления которого пропорциональна квадрату скорости движения. Найти время движения пули через брус.

Вариант 27

В примерах с 1 по 14 решить задачи в соответствии с условиями варианта задания:

в примерах 1- 9, 11 найти общее решение (общий интеграл) или частное решение дифференциального уравнения;

в примере 10 написать общее решение дифференциального уравнения

со специальной правой частью, не находя числовых значений неопределенных коэффициентов частного решения;

в примерах 13-14 решить геометрическую и физическую задачу, путем составления дифференциального уравнения.

27.11 ex yy ex ; y 0 1.

27.2xdy ydx ydy.

27.3 xy 2x2

y 4y.

27.43x2 6xy2 dx 6x2 y 4y3 dy 0.

27.5y xsinx; y 0 y 0 y 0 0 .

27.6x2 y '' y ' 2

27.7	y	y	;		0 2.

		y
				y 0 1,y

27.8y 2y y 0; y 0 0,y 0 2,y 0 3.

27.9y 4y xsin2x .

27.10y 4y 3ex sin2x 7cos2x.

27.11y y secx.

27.12 y x e y ;

y 0 0.

27.13 В точке с ординатой 2 кривая наклонена к оси Oy под углом 45 . Любая

ее касательная отсекает на оси абсцисс отрезок, равный по длине квадрату ординаты точки касания. Записать уравнение данной кривой.

27.14 Круглый цилиндрический бак с вертикальной осью, диаметром 2R и высотой H наполнен водой. Из бака вода вытекает через круглое отверстие диаметром 2a в дне бака. Определить время опорожнения бака.

Вариант 28

В примерах с 1 по 14 решить задачи в соответствии с условиями варианта задания:

в примерах 1- 9, 11 найти общее решение (общий интеграл) или частное решение дифференциального уравнения;

в примере 10 написать общее решение дифференциального уравнения

со специальной правой частью, не находя числовых значений неопределенных коэффициентов частного решения;

в примерах 13-14 решить геометрическую и физическую задачу, путем составления дифференциального уравнения.

28.13ex tgydx 1 ex dy 0. cos2 y

28.22x3y y(2x2 y2).

28.3x2 xy y; y 1 0.

28.4sin2y x x dx y siny22x dy 0.

28.5x2 y xy 1.

28.6x 1 y x 2 y x 2 0.

28.7y 1 y 2 ; y 0 y 0 0.

28.8y y y y 0; y 0 1,y 0 0,y 0 1.

28.9y 4y 3y xex .

28.10y y x2 3 ex 6sinx 3cosx .

28.11y y 1/ ex 2 .

28.12 y y y 2 y3 x;

y 0 1, y 0 0,5.

28.13Кривая y y(x) проходит через начало координат. Середина отрезка ее нормали, заключенного между любой точкой кривой и осью абсцисс, лежит на параболе y2 ax . Составить уравнение указанной кривой.

28.14Моторная лодка движется в спокойной воде со скоростью v0 20км/ч. На

полном ходу ее мотор выключается и через 40 с после этого скорость лодки уменьшается до v1 8км/ч. Сопротивление воды пропорционально скорости

движения лодки. Определить скорость лодки через 2 мин после остановки мотора.

Вариант 29

В примерах с 1 по 14 решить задачи в соответствии с условиями варианта задания:

в примерах 1- 9, 11 найти общее решение (общий интеграл) или частное решение дифференциального уравнения;

в примере 10 написать общее решение дифференциального уравнения

со специальной правой частью, не находя числовых значений неопределенных коэффициентов частного решения;

в примерах 13-14 решить геометрическую и физическую задачу, путем составления дифференциального уравнения.


29.1	y cos x 2y cos x 2y ; y 0 /4.
29.2	xy y			y2		x2 .
29.3	x y y ex .
29.4			xdy			y
			xdy			y		1 dx.
		x	2 2		2	y	2	1 dx.
		x	y	x		y

29.5y yx .

29.6x y 1 y 0.

29.7	yy				2	;		0 1.
			2yy lny y				y 0 y

29.8y IV 5y 4y 0; y 0 1,y 0 4,y 0 1, y 0 16.

29.9y 2y 2y e xcosx.

29.10y y 2ex 2sinx 6cosx.

29.11y 4y 1/sin2x.

29.12 y y cos x 2cos y;

y 0 0.

29.13 Кривая y y(x) проходит через точку (0;1) и обладает тем свойством, что

в каждой ее точке тангенс угла касательной к этой кривой равен удвоенному произведению координат точки касания. Найти кривую y y(x).

29.14 Определить время, необходимое для установления одинакового уровня жидкости в сообщающихся сосудах, если в начальный момент уровень жидкости в первом сосуде находился на высоте h1 от отверстия, а во втором – на высоте

h2 h1 h2 .Площадь горизонтального сечения первого сосуда равна S1, второго - S2 , а площадь отверстия – s.

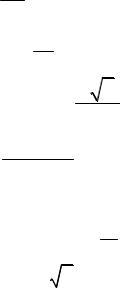
Вариант 30

В примерах с 1 по 14 решить задачи в соответствии с условиями варианта задания:

в примерах 1- 9, 11 найти общее решение (общий интеграл) или частное решение дифференциального уравнения;

в примере 10 написать общее решение дифференциального уравнения

со специальной правой частью, не находя числовых значений неопределенных коэффициентов частного решения;

в примерах 13-14 решить геометрическую и физическую задачу, путем составления дифференциального уравнения.

30.1yyx ey 0; y 1 0.

30.2y xy22 2.

30.3y 2xy cos2 2yx .

30.42 x2 2 y dx 2dy 0.

30.5y 1/ 1 x2 ; y 0 y 0 0

30.6y 1 ln x yx' 2 ln x;y 1 12, y ' 1 1

30.7 y 1/

y; y 0 y 0 0.

30.8y IV 10y 9y 0; y 0 1,y 0 3,y 0 9,y 0 27.

30.9y y cos2x.

30.10y y 2x 5 ex 6cosx 5sinx.

30.11y y ex / ex 1 .

30.12	y yex x y 2 ; y 0 1, y 0 y 0 1.
30.13	Кривая проходит через начало координат и лежит в полуплоскости y 0.

Каждый прямоугольник, ограниченный осями координат и перпендикулярами к ним, делится на две части, причем площадь части прямоугольника, находящейся под кривой, в 2 раза меньше площади части прямоугольника, находящейся над кривой. Найти уравнение кривой.

30.14 Цепь длиной L = 4 м соскальзывает с гладкого горизонтального стола. В начальный момент движения со стола свисал конец цепи длиной а = 0,5 м. Пренебрегая трением, найти время соскальзывания всей цепи по столу.

4. Решение типового варианта

1. y 3x 2y 5

Уравнение сводится к уравнению с разделяющимся переменными путем замены

u 3x 2y 5, где u u(x) новая неизвестная функция;

2y 3x u 5;

y 23 x 12u 52 ;

y 23 12u . Тогда уравнение примет вид

23 12u u ;

12u 23 u ; u 3 2u .

Разделяем переменные:

3 2u

;

dx .

d (3 2u)

Интегрируем обе части:

dx c ;

x c ;

1ln

3 2u

x c ; ln

3 2u

2x c

, (где

2c новая произвольная

постоянная);

3 2u

e 2x c1

e 2x ec1

e 2xc

; 3 2u c

e 2x c

e 2x ( c

ec1

положительная постоянная,

постоянная любого знака)

2u 3 c e 2x

;

u 3 1c e 2x y 3 x 1

1c e 2x 5

3 x

1c e 2x

5 3, или,

2 2

2 4

обозначая 14c3 как новую произвольную постоянную c , y ce 2x 32 x 74 –

общее решение исходного уравнения (легко проверить, что при c 0 это тоже решение этого уравнения).

2. xy y (x y)ln

x y

; y(1) e 1

Разделим обе части уравнения на x :

. Теперь видно, что

ln 1

уравнение является однородным и решается путем замены u

, где u u(x)

новая неизвестная функция. y ux ; y u x u

и уравнение примет вид

u x u u (1 u)ln(1 u);

u x (1 u)ln(1 u). Решаем полученное уравнение с

разделяющимися переменными: du x (1 u)ln(1 u);

dx ;

u)ln(1 u)

dx c ;

d ln(1 u) ln

(записываем произвольную

(1 u)ln(1 u)

ln(1 u)

постоянную в таком виде); ln

ln(1 u)

c2x

;

ln(1 u)

c2x

;

ln(1 u) c2x ,

или ln(1 u) cx ( c2

с произвольная постоянная); 1 u ecx ; u ecx 1;

y ux x(ecx 1). Для решения исходной задачи Коши подставим в эту формулу

x 1: 1(ec 1) e 1 ec e ;

c 1 y x(ex 1).

3. y (2x y3)y

По теореме о производной обратной функции y yx

. Тогда

y (2x y3)

; x y 2x y3 ;

x y2 . Последнее уравнение является

линейным по x , находим из него x

как функцию от y : x x(y), используя,

например, метод Бернулли решения линейных уравнений. А именно, ищем

функцию x

в виде x uv , где u u(y),

v v(y). Тогда x

u v uv

; u v

u v

. Для нахождения функции v потребуем,

чтобы v

v 0.

Из этого уравнения с разделяющимися переменными dv

v ;

dy ;

dv 2

dy c ; ln

2ln

; ln

cy2

; v cy2

. Так как нам

достаточно знать хотя бы одну такую функцию v , то положим в последнем

равенстве c 1:v y2 . При такой функции v получаем для u u(y)

уравнение

u v y2 ;

u y2 y2 ;

u 1 u(y) 1dy y c и x uv (y c)y2 . Таким образом,

общий интеграл исходного уравнения имеет вид y3 cy2 x 0.

2 dx (x

1)cos y dy 0

sin y

cos2y 1

Проверим, что это уравнение является уравнением в полных дифференциалах:

x cos y

;

sin y

sin2 y

(x2 1)cos y

2x cos y

x cos y

. Тогда исходное

cos2y 1

2sin2 y

sin2 y

cos2y 1

уравнение можно записать в виде du 0 , и общий интеграл этого уравнения имеет вид u(x, y) c . Для нахождения функции u используем формулу

x	y
u(x,y) P(x,y)dy Q(x0,y)dy .
x0	y0

В качестве точки (x0, y0 ) можно взять любую точку, в которой функции P(x,y)

Q(x,y) непрерывны вместе со своими частными производными. Возьмем, например, x0 0, y0 2 . Тогда

u(x,y) x

dx y

cos y

1 y d sin y

cos2y 1

2 sin

0 sin y

2sin y

1 . Таким образом, общий

2sin y

интеграл

исходного уравнения имеет вид

c , или

2sin y

x2 4x sin y 1 (2c 1)sin y 0 , или, беря

2c 1 за новую постоянную,

x2 1 (4x c)sin y 0 .

2xy y y 2 4; y( 1)

8,8; y ( 1) 3

В уравнении отсутствует неизвестная функция y , поэтому порядок уравнения можно понизить путем замены y z , где z z(x) новая неизвестная функция. Тогда y z и уравнение примет вид 2xzz z2 1. Это уравнение с разделяющимися переменными и решается как все такие уравнения:

;

2zdz

;

2xz dx

z2 4

;

z2 4

;

z2 4 c x ; z

	d(z2 4)	ln x ln c ;
	z2 4

c1x 4 . Таким образом,

c1x 4 . Подставляя сюда

x 1, имеем:

4 c1 . Значит, знак перед

корнем должен быть «–» и 9 4 c1 ;

c1 5 y

4 5x . Интегрируем по x :

4 5xdx c2 15

4 5xd (4 5x) c2

1 2(4 5x)2

(4 5x)3 c

. Подставим в это равенство

x 1:

8,8

27 c

(4 5x)3

26 – общее

решение исходного уравнения.

6. xy y 2xy 2

В уравнении, опять-таки, отсутствует x , поэтому сделаем замену

y z , где

z z(x) новая неизвестная функция, уравнение для которой имеет вид

2xz

; z x 2z

. Это уравнение Бернулли. Будем решать его методом

вариации произвольной постоянной. Решим соответствующее однородное

уравнение

: dx

; z

x ;

c ;

; ln

;

z cx .Теперь будем искать решение уравнения Бернулли по той же формуле

z cx , считая, что в ней c c(x). Тогда

;

c 2c

;

z c x c x

c x

dx x 2c

;

2xdx ;

2xdx c1 ; c

c1 ;

x2 c

d(x2 c )

Таким образом y

и y

x2 c

12ln x2 c1 c2 . Итак общее решение исходного уравнения имеет вид y 12ln x2 c1 c2 .

7. y4 y3 y 1 0; y(0)	2; y (0)	2
		2

Так как в уравнении отсутствует независимая переменная x , то сделаем замену

y z , где z z(y) новая неизвестная функция (то есть

y становится

переменной, а z ищется как функция от y ). Тогда

y (yx )x (yx )y

z z

zdz

y4 1

уравнение принимает вид y

z z 1

0 ; y

; dy

. Разделяем

переменные:

y4 1

c ;

zdz

c; z2

( 2c

произвольная постоянная);

2y2

y 2 y2

c . Из этого равенства найдем знак перед корнем и

постоянную c , используя оба начальных условия: при x 0

1 c

знак «+», возводим обе части в квадрат: 12 2 12 c1 c1 2 и

y	y2	1	2			1	2		1		. В окрестности точки				x 0 выражение

					y			y
		2				y			y
		y
1	0, так как					1		2		1		0, тогда	y	1		y2	1	. Опять
y y				y(0) y(0)						2				y y			y

100

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1110 11 > Следующая >>>

Соседние файлы в предмете Высшая математика

#
05.12.20241.48 Mб1Билеты экзамен.pdf
#
04.12.2024950.34 Кб1Вышмат.pdf
#
04.12.202412.93 Mб36ОТВЕТЫ К ЗАЧЕТУ 1 СЕМ.docx
#
04.12.202416.63 Кб2Список вопросов для экзамена по высшей математике.docx