I: Interval of stiffeners (cm)

IT Do'

^a= 2/

say a²< 1 approximately

p* = 2.4£

= 0, but simi- dn

Number of wrinkles (n) is obtained from

larly to the above, an integer closest to the value obtained from the following formula can be taken:

n = 1.63

I Do' \o sfDo' \°-²ⁱ ( I I \ H

R.V. Southwell’s formula

_E,/( tt⁴ /r«\⁴ «²-l pV

^P* r„(n*(n²-l) ( /) 12(1 - r?) \.rj

Say n² - 1 = n² approximately

P‘=²-^59£-7&^: .

2) Stiffeners

24E,Z

^Pk~ (l-p?)Do'³/

where I: Moment of inertia of combined sections of stiffeners (cm⁴)

1. 

   pressure

   Tensile stress due to internal

PD PD

^a~ 2t ^Or 2(/o-c)

where a: Stress (kgf/cm²)

. P: Maximum hydraulic pressure at a place to determine stress (kgf/cm²)

Tensile stress is generally calculated by the above formula. When bedrocks are strong enough to share part of the internal pressure, cal­culation should be made by the following equation.

where X: Sharing ratio of internal pressure by bedrock

E_s: Elastic modulus of steel (=2.1 x 10⁶ kgf/cnri) a_s: Coefficient of linear expansion of steel (= 1.2 x 10~V°C)

AT: Temperature change of steel penstock (= 0~20°C) Coefficient of plastic deformation of concrete (permissi­ble to take as = 0)

E_c: Elastic modulus of concrete (=2.1 x 10⁵ kgf/cm²)

D^. Excavation diameter of tunnel (cm)

0/. Coefficient of plastic deformation of bedrock

E_t: Elastic modulus of bedrock (kgf/cm²) m_g: Poisson’s number of bedrock (= 5) is usually taken as 0.5.

Sharing ratio of internal pressure by bedrock differs greatly depend­ing on the physical properties of bedrock, initial gaps between a pen­stock and concrete and so forth.

If bedrock is sound with no cracks, and its elastic modulus is fairly large, it can share the internal pressure to a great extent.

But there are a lot of unknown factors in bedrock. It is not uniform ■' and there may exist such a defective portion as a partial dislocation. It is not always sure to secure a situation close to a theoretical compu­tation. Therefore, a condition to the effect that “the pipe shell stress due to the internal pressure should not exceed the yield point of material even if it is assumed that the bedrock does not share an internal pres­sure,” is provided in many cases. Examples of the above are listed in Table 1.16-2.

Table 1.16-2 Example of Pressure Shared by Bedrock

Power station	! Kiso	T" ■ ■ Kisenyama		Shintoyone		Okutataragi;Okuyoshinc			Shiniakase		Okujahagii ||oni,awa Tamahara No.2 . L.. 1 —						Shimogo
Power (MW)	116	466		1,125		1,212 : 1,206			1,280		780 I 600				I 1,200		1,000
	1								1 •				1
Effective head (m) Discharge (mJ/s)	225.9	220		203		383.4 ;Gen.) 376	! 505		230		I 404.6 ! 567.0				518		387
	(Gen.) 60	(Gen.) 248 (Pump) 220		(Gen.) 645 (Pump) 600			(Gen.) 288		(Gen.) 644i|(Gen.) 234			| (Gen.) 140		(Gen.) 276 (Pump) 210		(Gen.) 314 (Pump) 252
						(Pump) 25? JlPunip) 229.,			J — ♦		1 ...		■(Pump) 110
Number of penstock lines	1	2		5		4 6 «									4		4
									4		J		2
Max. design head (m)	306	350		364		630	840		380		620		815		827		620
Internal diameter (m)	4.0-3.2	5.9-4.5 3.4		5.0 J.8 (No. 1, 2)		6.3-4.9 3.45-2.5	53-4.3 2.7-I.8		8.0-5.65 3.3		6.2 3.2		. 6.0-4.9 3.5-2.I •		5.5—4.2 2.9-2.1		5.7-4.4 2.9-2.3
Length (m)	249.3	342.1		313.6		641.3	786.7		336.4		850.8		921.3		916.6		719.3
Length of pressure shared by bedrock (m)	78	46		110		Nearly whole! 457 length			2+4.4 J		278		1 220.9		200		667
Design sharing ratio of internal pressure («?.)	40	26.3		40		35-48	r ■ ■ ■ 22-31		58-6?		24-47		14-22		22-41		20-45
Aciuai sharing ratio of internal pressure (%)	69-75	. 62-68		81-89		57-88	50-70		—■		■ —■•		—		—		—
Design clastic modulus of bedrock (kgf/nr)	30,000	20,000		75,000		30,000- 50,000	30,000-- 40,000		60,000		14,000- 60,000		25,000		30,000- 50,000		30,000- 60,000
Pipe shell material	HW45	SM50B SM58Q		SM58Q		SM50B SM58Q i	SM50B SM58Q HT80		SM50B SM58Q		SM50B SM58Q HT80		SM4IB SM58Q HT80		SM50B SM58Q HT80		SM58Q
Year of completion	1968	1970		1972		1975	1980		1981		1981		Under construc­tion		Under construc­tion		Under construc­tion

2. Local bending stress due to the restraint of the pipe shell displacement by means of stiffeners.

where A;. Ring’s sectional area = l,h_r + r(1.56V7^r + t_r) (cm²)

Fig. 1.16-4 Stiffener’s Section

3. Temperature stress

where a_t2: Stress due to temperature change (kgf/cm²) a: Coefficient of linear expansion (1.2 x 10^_5/°C) E: Elastic modulus of steel 2.1 x 10⁶ (kgf/cm²)

AT: Temperature change (°C)

4. Stress due to Poisson’s effect

Because of restraint of longitudinal displacement of a pipe, longitu­dinal stress corresponding to the circumferential stress is generated by Poisson’s effect.

where a_n: Stress due to Poisson’s effect (kgf/cm²) v: Poisson’s ratio of steel (= 0.3) o_r: Circumferential stress (kgf/cm²)

PD n a_r= (1 -X)

2t

5. Stress due to external pressure and critical buckling pressure

(1) Without stiffeners

E. Amstutz’s formula is generally used. In addition, E.W. Vaughan’s formula and Montel’s formula are also used. Vaughan’s formula is the one to have modified Amstutz’s analysis, and Mon­tel’s formula is an empirical equationby assuming that the buck­ling is largely affected by an error of “out of roundness”.

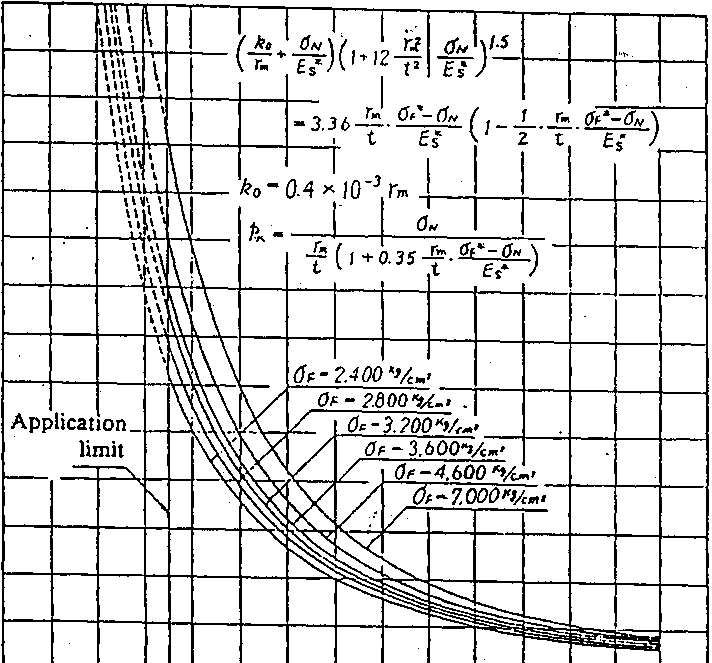
E. Amstutz’s formula (this formula conforms to an actual case within the range of Zel>35)

f k₀ . a_N \ | _t r_m² oh V^s

t² ’&¹/ -

. - ^r_m ctf -on . 1 r_m <j_F*-a_N\

t E_s* \ 2 t E* ]

where k$. Gap between concrete and external surface of pipe (cm). k_Q is usually taken as 0.4 x 10"³r_m.

(cwlT+U^V.-

where a_a: Allowable stress of material (kgf/cm²)

■q: Joint efficiency

u_N: Circumferential direct stress at deformed pipe shell portion (kgf/cm²)

On

With o_N given from this formula, pk can be determined by the following equation:

Pk =

—11+0.35— °^F

f \ t Dr

: %C>1

140

120

100

QO

60

40

20

140

O0 a a o

0 20 40 60 50 100 120

Ratio of embedded pipe’s radius to shell thickness (r_m/t)

Fig. 1.16-5 Critical Buckling Pressures of Embedded Pipes without Stiffeners (by E. Amstutz’s formula).

E;W. Vaughan’s Formula

0F Oct , I /Cq Oct \ l"m

i I'm Op Q_cr

¹ t 24o_c, ^=U

2E_t* op- OcA r_m ⁺ E/ )] t²

Montel’s formula

where u: Relative error of a radius measured with the range of a. 5jO° center angle (cm)

. _;, _t J: Gap between concrete and external surface of pipe (cm) (2) With, stiffeners

A. Pipe shell proper

S. Timostjepko’s formula is generally used.

S. Timoshenko’s formula

. 2n^z-\-v_s\

^1+-TT

7r²/o

p? ' t^{2 3 4}

' 'I ■ ]

x«i~(i+n—

■ i. fr*

1.56*Jr_mz

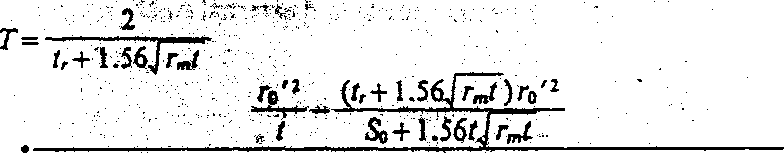
3 Irt)' \^u sinh ffl+sin 0/ 2r_o^z2

[3(lrr.?)l’’^!\ > I cosh 0/-COS 0/ ⁺ So+1.56/Jr„r ^3=—

Sar»tr(t±h^ , . _i -

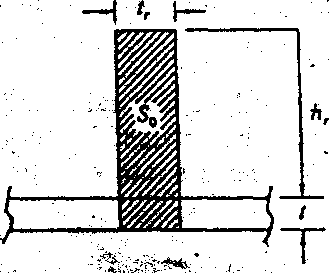
Fig. 1.16-6 . Cross Section of Stiffener

where Modified interval of stiffeners (cm)