Метод Т-матриц / download

BiCGScattering-FFTSolutionT-MatrixfromMethodInhomogeneousfor Solving Bodiesfor the

J. H. Lin and W. C. Chew

y

Electromagnetics Labora

Department of Electrical and Computetor Engineering

University of Illinois

Urbana, IL 61801

Abstract

ciently solv

three

A BiCG-FFT T-Matrix algorithm is prop sed to

scattering problems of inhomogene us bodi

. The memory stor-

dimensionalbo of various size

are shown.

It is also

demonstrated

that the matrix

condition

umber for ne grids is

the same as that for

coarse grids.

ge is of

(

) (N is the

umber of unknowns) and

each iteration in BiCG

requires

O(Nlog N) operations. A go d agr emen

between the numerical

xact solutions is observed. T

converg nce

rate

f

lossless and lossy

1. Introduction

c elds

y

bodies is a

T

scattering of

researcmethod of solving thelectromagnetinho oge eous body probleminhomogeneousby app ximating th

topic that nds applicatio

n man

elds. In this paper, w

bo y with

all

diel

ctric

cubes.

The dielectric cubespropose

then approximated by equivolume spheres [1-4]. In this

nner, the T matrix

[5,6] of eac

individual phere can be found in closed form. A set of

linear

inhomogeneousalgebraicrom ea of the spheres. By

using

T-ma rix

theamplitudesGreen'

method of moments, suc

easilysingularity has to be handled with c ution [7-9].

equations can

deriv

to solv for the scat ering

function singularity problem is

voided, while other form

s, such as

When the inhomogeneous

body thisdiscre ized

into ulation

ar grid,

res ltant equation has

block-Toeplitz structure.

An iterativ

solver suc

as BiCG (bi-c njugate

gradient) method [10,11]

be

to solve

is us d,

solution of the matrix equati

iteratively. Whencan iterativregulsolv

the main

of seeking the olution is the cost of performing mat ix-vec or

N is the total

m

of

spheres involved.

ultiplicati

. Exploiting the block-Toeplitz structure,usedw can peerform

90,000 unkn wns issholved on a Sparc 10 w

storage. I is shown

matrix-vectcostr

ltiplication in O(N

g N) operations b

FFT [7-9,12], wherthe

The

method can be

wn to require O(N) memory

. He

ce, it

can be u ed to s lvber fairly large

problems.

A volume

ering problem

because the matrix condition number for the formerorkstationcases scatsmaller than

withr tive

solvers converge faster for lossy bodies

an los less ones.

This is

for the latter ones, as a lossle

could hav

high

Q inte nal

modesA. the simulation results shobodyw, y using

the

T-

formulation,resonancethat

condition number of the resultant matrix is independenmatrixof the mesh size of

File:bicg tt.tex, Date:January 4, 1995

1

bodya

is gridded. Thnerefore,in orderthetoumbachievr ofbetteriterationsresolutiondoes not.

grow when the

2.uniformF ulation and Impl

mentation

uniform array, their scat-

When

umber of scatt rers are

placed on

tering solution

can be

obtained

e ciently by using FFT and an ite ativ

as The total

eld due to an

y of non-iden

scatterers can be written

method.

t

(karra;

X tical

E(r) =

)

+

N

(k ;

) b ;

(1)

i

=

?

0 and r0 is the location

center of the

-th

of the

0

s

s

=1

scatteringspherical

wherescatt rer. (k0;

0

or

) is a row vector containing the v

cident eld while

from

each

. The rst term in (1) comprises the

-scattererterer respe tively.

the second term

i

the

i

eld.

The vectors

and b

contain

is

tra slati

n

matrix

[4,13]scattereto hanged

he

coordinates of all the sphericalharmonics-

ampli udes of the inciden

eld harmonics and the scattered

eld

monicsocusthe

that of the j-th

to obtain

F

ing on

j-th

erer, w

can use the addition theorem or the

E(r) = <g

t

(k ;scatterer) a

<g

t

(k ; r )

N

b

0

j

js

s

0

j

X

ji

i

+

1

(k ; r

) b

(2)

Looking at the above, w

:i=6 j

that the

0woj

j

are inciden w v

impinging on the j-th

Therefore,

the third termsis the

scattered

eld

o the j-th scatterer.

the amplitude

of the third term must be

T matrix of

he j-th

scatterer,

. .,

T

.

Here,

T

is diagonalscattererfor th

related to the total amplitude of the rst

worst terms via the isolated

spherical

scatterer. Consequently,whilehave

j(1)

2

N

j(1)

3

6

7

b

= T

a

+

X

b

;

j = 1; ; N:

(3)

j

4

js

s

ji

i5

j(1)

1

Essentially, we

h the

i=6 j

condition at the surface of the j-th scat-

Equation (3) could beboundarewritteny

as

terer inst ad atmtheatcenter of the scatterer. This explains why this formulation

avoids the singularity probl m.

N

T

bj

? Tj(1)

X

ji

bi

=

j(1)

js as

(4)

1

2

i=6 j

or

B ?

T

A B =

T

S;

(5)

where

A

T and

are block matrices, and B and

S are block vectors whose

block elements are given by

T

;

a)

T]

=

ij

A]

ij

(6b

(1)

(6d)

[S]jij= js

s:

B]

;

if j =6

c

= b ;0;

otherwise;

(5) can be s lved w th iterative methods lik

the bi-conjugate gradi-

be in the matrix-vector m

A Bmajor. F a dense

rix, the cost of

suc

matrix-vector multipl plicationrequires O(N

2Mcomputational2) oper ions, where

M

Eisquationh dimension of the

matrices.

cost

ould

en (BiCG) method. In such

me hod, the

ij

grid, then

=

When the scattering centers are

(r ?rj ). The translation matrix is onlyplacedfunction ofiform?rj . When the for-

0

lock, the block-Toeplitz summationatrix is convertedEquation

Toeplitz-block matrix

0

sum

. I

such

0

0

ij

withulation

is imple

A

can be expressed as

m

ted, the

in

(4) is actually replaced

a block-Toeplitzdimensionalatrix. By grouping the elemencase,of same harmonics into

one(i. . eacthreeblock is T

. Then the fast Fourier tr

sform (FFT) meth

an be used to expedite the matrix-v

multiplication A B with operati n

count of O(NM logoeplitz)N .

ector , it possesses only electric dipole

If the

a

small c

matrix spheresdurthermto

orreo at onmparedsymmetry.

and

. Note th

0

circulan

matrixTherefore,in the x-

A has be n extended

oments whic cor

spond

the rst

hree harmonics in T .

the

In order to perform the

matrix-v

multipli

ation more e ciently

M = 3 and f

here

only 6 independen

ele

j(1)

ents in the 3 by 3

pr venstoredaliasing. Henc ,

nevcalculaer

matrix-vector m

is required

ij

to

y- and z-directions and zeros have ectorbe padded to the original vect

Fourier transform of

~

only once outside the iteration loop

A, A is

each

forward 3D-FFT correspondingultiplicationth ee

harmonics

nd nallyiterthation,ee inverse

3D-FFT are

carried

out. Then

the product can be

obtained

b disca ding thos

entries with zero-padding in the rst place.

re rst perfo med,thre

th y are multipli

~

the frequency domain

by A

The

memory requiremen

of the method is still O(N) since each block

matrix in A can be represented

by one of its rows or columns.

3. Results and Conclusions

both in Figure 1 for a dielectric layered

A good agreement is observ

sphere and in Figure 2 for a

dielectric3cube [9]. It converges in 53 iterations

References1] sectionJ. H Richmond,hape," IEEE\ScatteringT ans. AyntennasdielectricPropagatcylinder., vol.of13,arbitrarypp. 334cross-341,

arb

shaped bi logical

bodies," IEEE T ans. Microwav

The ry

dosimet

and scattering computation\Electromagneticof tor electromagnetic

elds,"

2]

1965

esay and K. M. Chen,

elds induc

inside

D. E.

3]

T. C.Guo, W. W. Guo and H. N. Oguz, \A

hnique for three-dimensional

IEEEtrarilyT

.

, vol. 29, no. 2, pp. 1636-1641, 1993.

4]

ch , Livol. 22, no. 12, pp. 1273-1280, 1974.

of T-matrix approach for

Y. M. W g and W. C. Chew, \ A

recursiv

5]

Antennas

opMagneticsga . vol

41, no. 12, pp. 1633-1639, 1993.

scattering,"

. C. WatePrman, \Matrix formulation

f

electromagnetic

the solutioansof elec romagnetic scattering by many spheres," IEEE T ans.

6

Pr c. IEEE

vol.

53, pp. 805-811, 1965.

W. C. Chew,

Waves and Fields in Inhomogeneous Media , Van N

[7]

Reinhold,

New Y

1990.

\Fast-F

ransf rm meth d fstrandthe

D. T. Borup and O. P.

calculation of SAR distributiGandhi, in nelyourierdisc tized

of biological

[8]

bodies," IEEE Tork, .

owave Theory Tech., vmodels. 32,

no.

4,

pp.

C. Y. Shen, K. J. Glover,Micr. I. Sancer and A. D. Varv

\ The dis-

crete Fourier

transform

method of solving di erential-in

equations

355-360, 1984.

rans. Antennas Propagat.atsis,vol. 37, no. 8,

in scattering theory," IEEE

pp. 1032-1041, 1989.

weak form

[9] P. Zwamborn and P. M. van den Berg, \The three-dimensio

of the conjugate g adient

FFT method for solving scatteritegraln problems,"

0]

IEEE T ans.

Micr

Theory T ch., vol.

40, no. 9, pp.

1757-1766,

R. Fletcher,

\Co

jugate gradien methods f

inde nite systems,"

Nu

erical Analysis Dundowave

1975, G.

. Watson, Ed. pp. 73-89, Springer-

1992.

of the generalized bi-conjugate gradien

T. K. Sarkar, \On the

ducting plates of

esonanapplicationsize using

the conjugate-gradien

meth

and

method,"

J. Ele

omagn.

Appl., vol. 1, no. 3, pp. 223-

1987.

[11]2

Verlag, New York, 1976.

M. F. Catedra,

J. G. CuevasWavesd L. Nu~no, \A scheme of analyze con-

recursivChew,aggregate T-matrix algorithm,"

in IEEE Antennas andadditionProp -

fast Fourierctransform," IEEE T ans. Antennas Propagat.242,vol. 36,

theory," J. Electromagn. Waves Appl. vol. 6, no. 2, pp. 133-142, 1992.

no

12, pp. 1744-1752, 1988.

[13]4

W.

C.

\Recurrence relation for three dimensional scalar

J. H. Lin and W. C. Chew, \A comparison of the CG-FFT method and the

gation Society International Symposium Digest, pp. 1591-1594, 1992.

5

30

25

20

15

(dB)

10

Bi−RCS

5

0

−5

−10

−15

−20

0

20

40

60

80

100

120

140

160

180

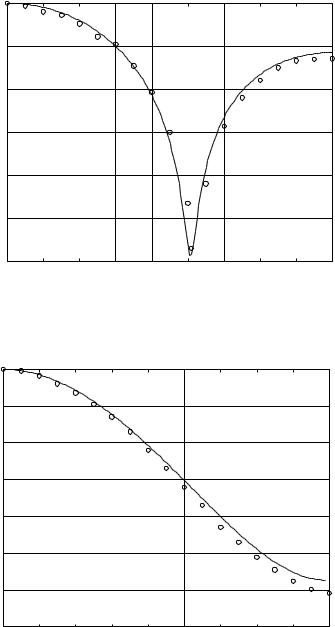
Figure 1. The Bi-RCS of a

theta layered scatterer. The solid

is

from the Mie series solution; the dash line is the numerical solution. lineH re,

b = 0:5

;

r1

= 1:2; a = 1:0

0

and

= 2:4. A 30 30 30 grid is used.

0

spherically2

6

= 0

0

−5

−10

dB −15

−20

−25

−30

20

40

60

80

100

120

140

160

180

0

theta (deg.)

(a) The far eld kE k as a function of

= 90

0

−1

−2

−3

dB

−4

−5

−6

−7

20

40

80

100

120

140

160

180

0

the

( eg.)

(b) The far eld kE k as a function of

Figure 2. The far elds as a function of

for a lossless dielectric

cube with r = 9

k0

= 60:628319: T

solid

the BiCG-FFT T-matrix method and the symbols represent the results by

Zwamborn and vandden Berg. A 7 7 7 gridcomputedislinesed.

7

number of iterations

102

Lossless medium

Lossy medium

101

102

103

104

105

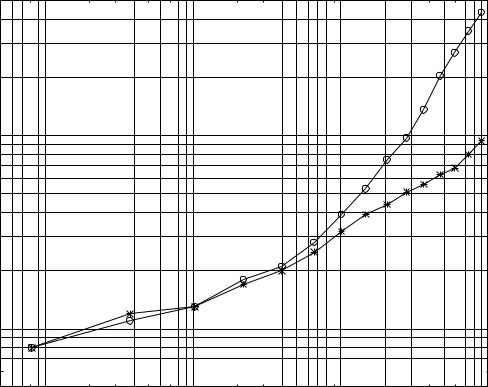
Figure 3. The

um

number of unknowns

of iterations vs. number of unknowns for lossless

cubes of r

= 9:0 and berfo

lossy cubes of r

= 9:0 + i3:0.

−260

−280

−300

−320

(dB)

Bi−RCS

−340

−360

−380

−400

−420

30

60

90

120

150

180

theta

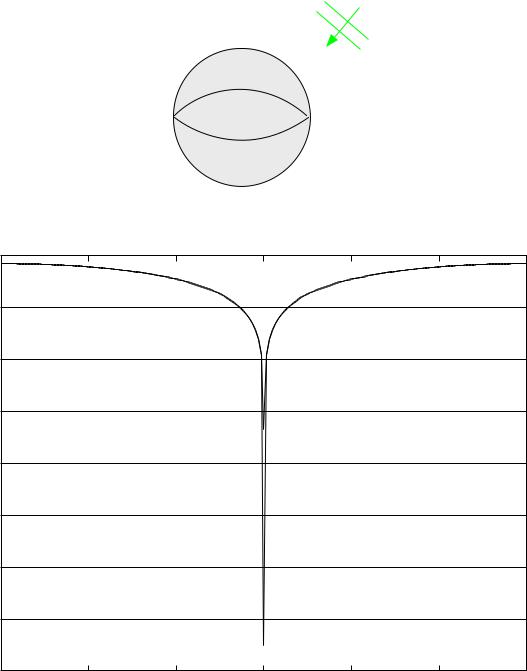
Figure 4. The Bi-RCS of a dielectric sphere. The solid line is from the Mie

series solution; the dash line is the numerical solution. Here, the radius =

?5

0

and r = 4:0. A 16 16 16 gird is used.

10

9