
глоссарий
.docxГЛОССАРИЙ
Элементы векторной алгебры
|
Понятие |
Содержание |
|
Вектор |
Направленный отрезок |
|
Модуль
вектора
|
Длина отрезка, изображающего вектор |
|
Коллинеарные
векторы
|
Если они лежат на одной прямой или на параллельных прямых |
|
Сонаправленные векторы |
Коллинеарные, направленные в одну строну |
|
Противоположные векторы |
Коллинеарные, равной длины, направленные в разные стороны |
|
Равные векторы |
Сонаправленые и одинаковой длины |
|
Единичный вектор |
Длина вектора равна единице |
|
Орт
вектора
|
Единичный
вектор, сонаправленный вектору
|
|
Проекция
вектора
|
Число,
определяемое по формуле
|
|
Координаты вектора |
Проекции вектора на оси системы координат |
|
Скалярное
произведение векторов
|
Число,
равное произведению длин этих векторов
на косинус угла между ними:
|
Аналитическая геометрия на плоскости
|
Понятие |
Содержание |
|
Прямоугольная система координат |
Задается двумя на плоскости и тремя в пространстве взаимно перпендикулярными числовыми осями (ось абсцисс, ось ординат, ось аппликат) |
|
Полярная система координат |
Задается выходящим из полюса лучом (полярная ось) с масштабным отрезком |
|
Окружность |
Множество точек на плоскости, равноудаленных от точки, называемой центром окружности |
|
Эллипс |
Множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, большая чем расстояние между фокусами |
|
Гипербола |
Множество точек плоскости, разность расстояний от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, меньшая чем расстояние между фокусами |
|
Парабола |
Множество точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой |
Введение в математический анализ
|
Понятие |
Содержание |
|
Функция y=f(x) |
Зависимость
f,
при которой каждому x |
|
Числовая последовательность xn |
Функция, заданная на множестве натуральных чисел xn=f(n) |
|
Предел числовой последовательности xn |
Число
а,
если для любого положительного числа
ε найдется такое натуральное число
N,
что при всех
n>N
выполняется |
xn
–
а|<
ε. Записывают
|
|
Сходящаяся числовая последовательность |
Имеет предел, причем всегда единственный |
|
Предел
функции f(x)
в точке xo,
т.е.
|
число А, если для любого положительного числа ε найдется положительное число δ, что при всех x: |x-xo|< δ, x≠xo выполняется неравенство |f(x)-A|< ε; |
|
y=f(x) непрерывная в точке xo |
Если
существует предел функции в этой точке
и он равен значению функции в этой
точке:
|
|
Производная функции y=f(x) в точке x |
Предел
отношения приращения функции к
приращению аргумента, когда приращение
аргумента стремится к нулю:
|
|
Дифференциал функции y=f(x) в точке x |
Главная
часть приращения функции:
|
Интегральное исчисление
|
Первообразная функции f(x) на интервале (a;b) |
Функция
F(x):
|
|
Неопределенный интеграл от функции f(x) |
Совокупность
всех первообразных функции f(x).
|
|
Определенный интеграл от f(x) на [a;b] |
Число
I,
как предел интегральной суммы, не
зависящий ни от способа разбиения
отрезка [a;b]
на частичные отрезки, ни от выбора в
них точек
|
|
Несобственные интегралы |
Определенные интегралы от непрерывной функции, но с бесконечным промежутком интегрирования или определенный интеграл с конечным промежутком интегрирования, но от функции, имеющей на нем бесконечный разрыв |
Дифференциальные уравнения
|
Понятие |
Содержание |
|
Дифференциальное уравнение (ДУ) |
Уравнение, связывающее независимую переменную, искомую функцию и ее производные |
|
Решение ДУ |
Функция, которая при подстановке в уравнение обращает его в верное тождество |
|
Порядок ДУ |
Порядок наивысшей производной, входящей в ДУ |
|
Интегральная кривая ДУ |
График всякого решения ДУ |
|
ДУ первого порядка |
Уравнение,
связывающее независимую переменную,
искомую функцию и ее производную:
|
|
ДУ второго порядка |
Уравнение
вида:
|
|
Общее решение ДУ первого порядка |
Функция
|
|
ДУсРП |
Уравнение
вида:
|
|
ОДУ первого порядка |
Уравнение
|
|
ЛДУ первого порядка |
Уравнение
вида:
|
|
ЛОДУ 2-го порядка с постоянными коэффициент. |
|
|
ЛНДУ второго порядка |
|
Комплексные числа
|
Понятия |
Содержание |
|
Комплексное число z |
Выражение
вида z=x+iy
(алгебраическая
форма),
i2
=
-1, x;y |
|
Тригонометрическая форма комплексного числа |
|

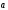
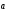 и
и
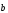
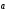
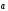
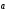 на ось l
на ось l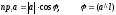
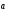 и
и
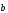

 D
ставится в соответствие единственное
значение y
D
ставится в соответствие единственное
значение y E
E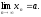
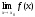
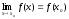
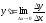
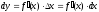

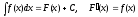
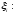
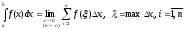
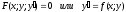
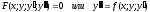
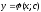 ,
которая является решением ДУ при
каждом с
(с=const),
и для любого начального условия
,
которая является решением ДУ при
каждом с
(с=const),
и для любого начального условия
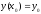 константа
константа
 определяется однозначно
определяется однозначно
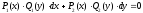
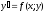 ,
если f(x;y
) – однород.
функция нулевого порядка, т.е.
,
если f(x;y
) – однород.
функция нулевого порядка, т.е.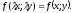
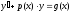

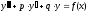
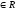
 модуль
и аргумент комплексного числа.
модуль
и аргумент комплексного числа.