
Лабы (Мосичев) / Лабораторная работа №31
.docxМинистерство цифрового развития, связи и массовых коммуникаций российской федерации
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
(МТУСИ)
Кафедра теории электрических цепей
Лабораторная работа №31
по дисциплине
«Электротехника»
на тему
Исследование на ЭВМ характеристик источника постоянного напряжения
Выполнил: студент группы БББ0000 факультета ИТ Фамилия И.О.
Проверил: к.т.н. Мосичев А.В.
Москва 2023г.
Цель работы:
С помощью программы Micro-Cap исследовать входные амплитудно-частотные (АЧХ) и фазочастотные (ФЧХ) характеристики RL-цепи. Сравнить АЧХ и ФЧХ, полученные с помощью программы Micro-Cap, с аналогичными характеристиками, полученными расчетным путем.
Исходные данные:
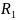 = 129 Ом – сопротивление резистора;
= 129 Ом – сопротивление резистора;
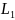 = 45 мГн – индуктивность катушки;
= 45 мГн – индуктивность катушки;
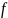 = 2, 4, 6, 8, 10, 12, 14 кГц – частоты;
= 2, 4, 6, 8, 10, 12, 14 кГц – частоты;
Е = 0,9 В – действующая ЭДС источника гармонического сигнала.
Расчётные формулы:
Модуль и фаза входного сопротивления:
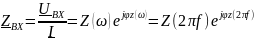 ,
,
где
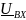 – комплексное входное напряжение;
– комплексное входное напряжение;
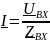 – комплексный входной ток;
– комплексный входной ток;
UR = R • I – комплексное напряжение на резисторе;
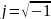 – мнимая единица;
– мнимая единица;
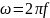 – угловая частота;
– угловая частота;
f – частота;
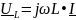 – комплексное напряжение на катушке;
– комплексное напряжение на катушке;
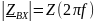 – модуль комплексного входного
сопротивления (АЧХ);
– модуль комплексного входного
сопротивления (АЧХ);
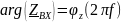 – аргумент (фаза) комплексного входного
сопротивления (ФЧХ).
– аргумент (фаза) комплексного входного
сопротивления (ФЧХ).
С другой стороны, входное сопротивление – это сопротивление со стороны входных зажимов:
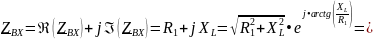
 ,
где
,
где
Re(ZBX) = R1 – резистивное входное сопротивление (равно сопротивлению резистора R1),
Im(ZBX) = XL – реактивное входное сопротивление,
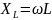 – индуктивное сопротивление катушки
L1.
– индуктивное сопротивление катушки
L1.
fгр =
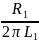 – граничная частота RL-цепи.
– граничная частота RL-цепи.
Предварительный расчёт
Проведём предварительный расчёт и построим графики в программе Scilab.
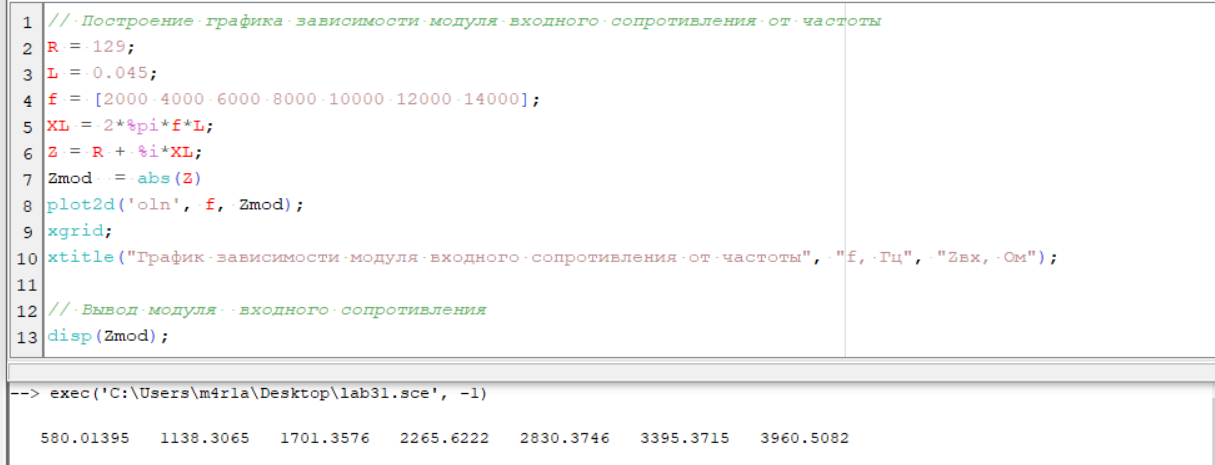
Рисунок 1 – Вычисление и вывод модуля входного сопротивления, построение графика
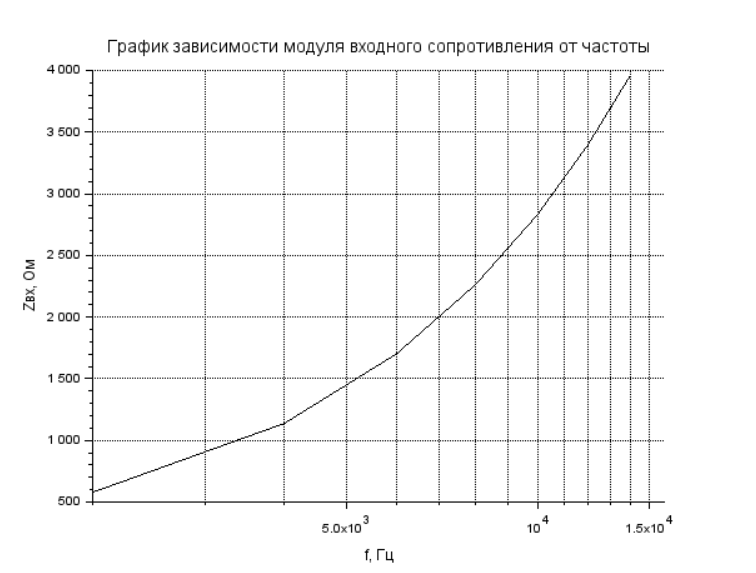
Рисунок 2 – График зависимости модуля выходного сопротивления от частоты
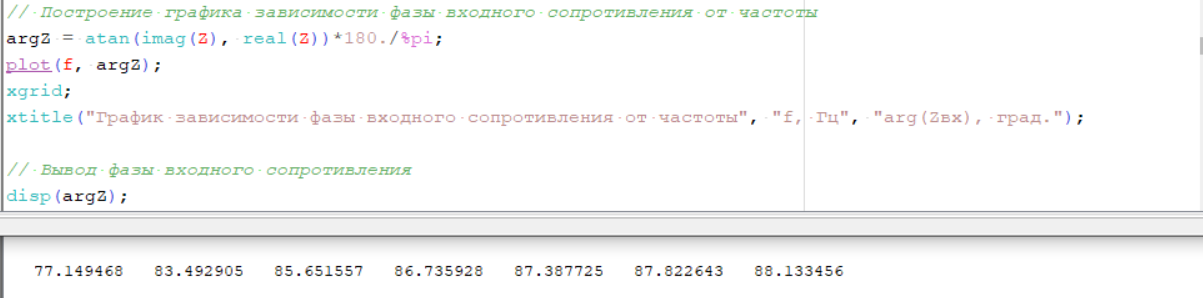
Рисунок 3 – Вычисление и вывод фазы входного сопротивления, построение графика
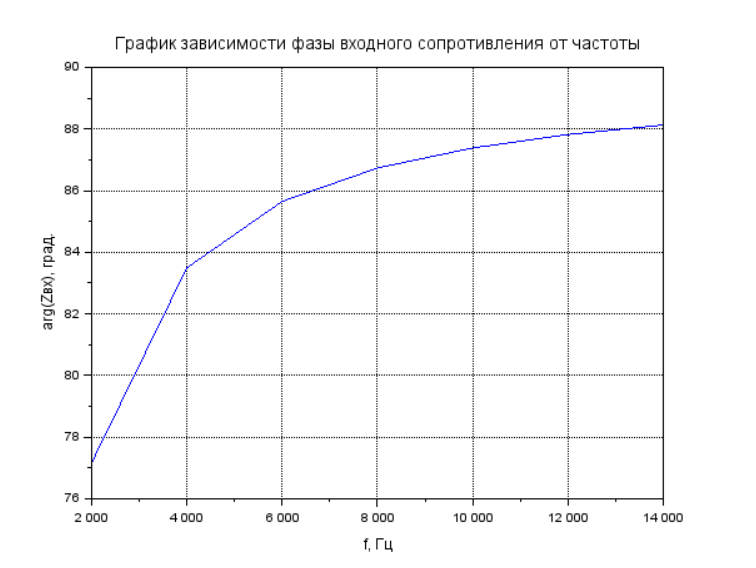
Рисунок 4 – График зависимости фазы выходного сопротивления от частоты
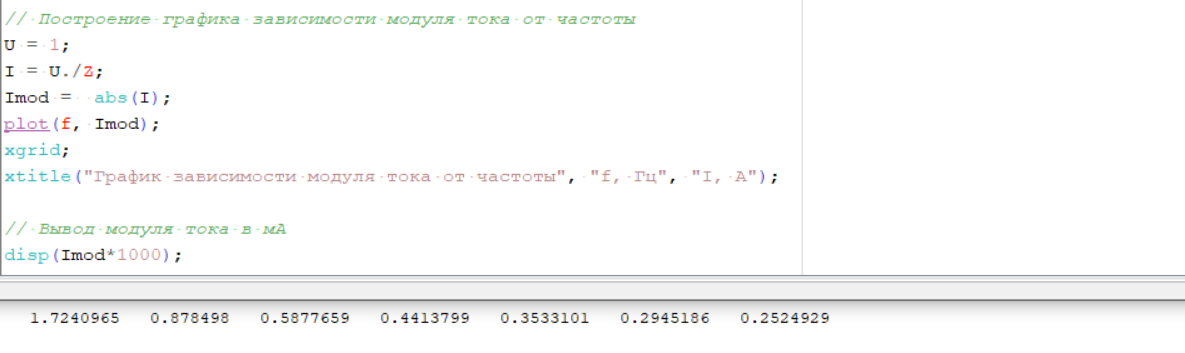
Рисунок 5 – Вычисление и вывод модуля тока, построение графика
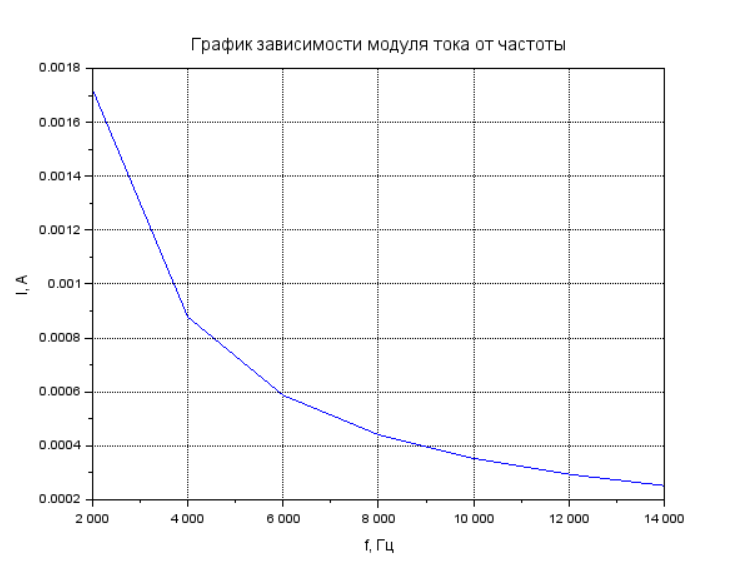
Рисунок 6 – График зависимости модуля тока от частоты
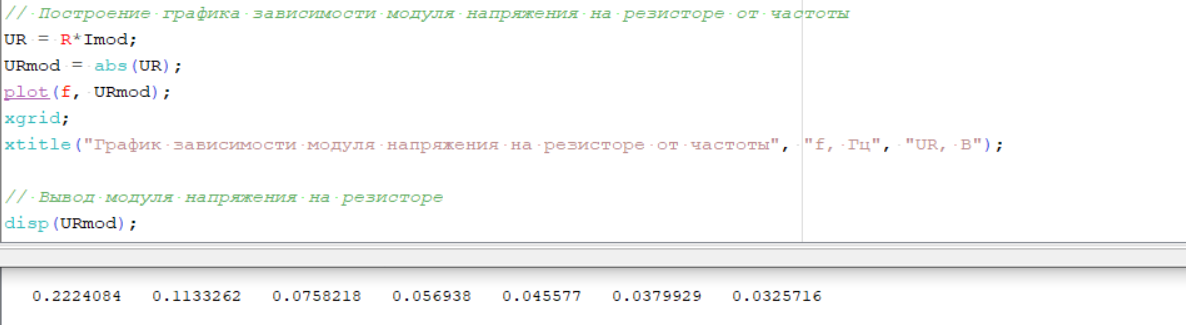
Рисунок 7 – Вычисление и вывод модуля напряжения на резисторе, построение графика
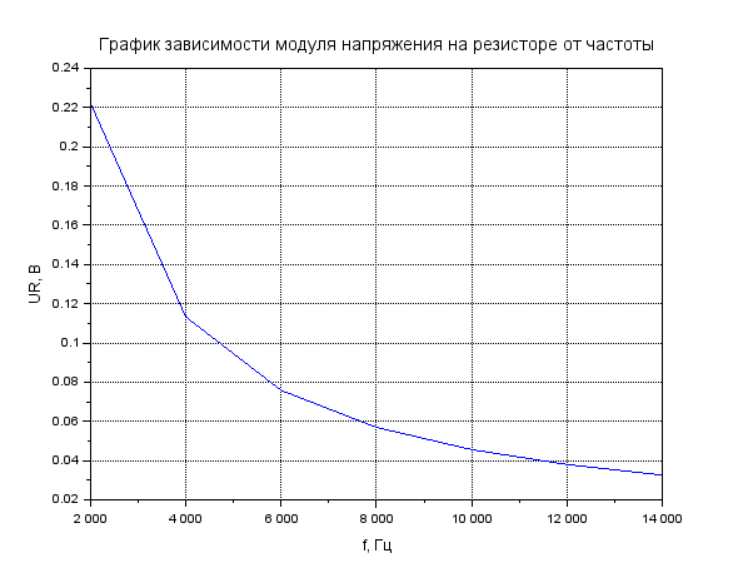
Рисунок 8 – График зависимости модуля напряжения на резисторе от частоты

Рисунок 9 – Вычисление и вывод резистивного сопротивления, построение графика
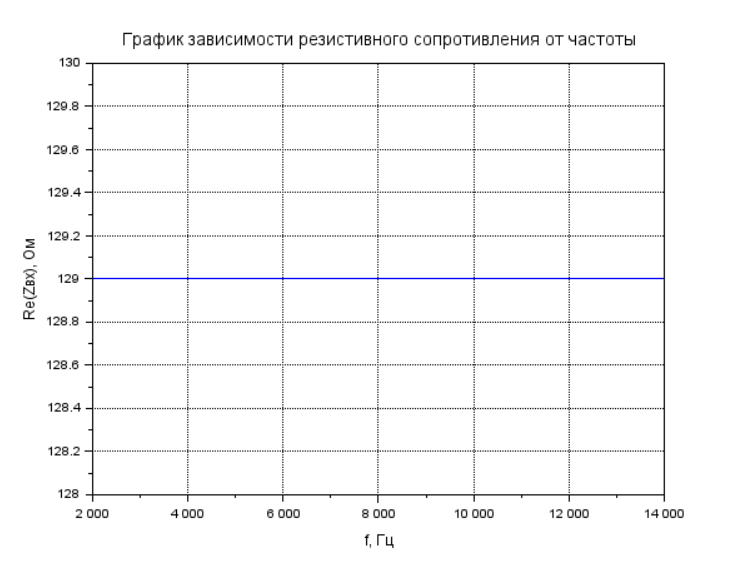
Рисунок 10 – График зависимости резистивного сопротивления от частоты
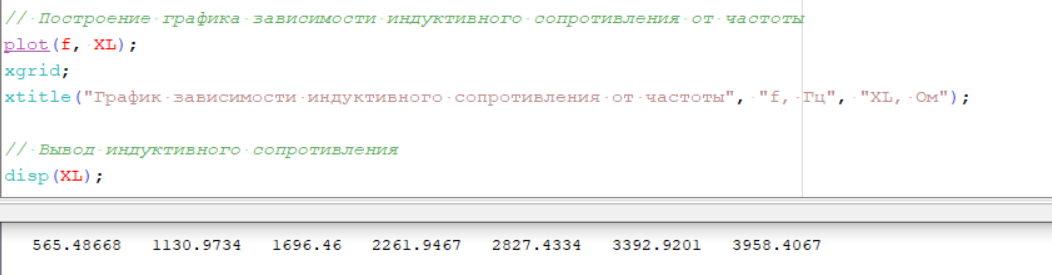
Рисунок 11 – Вычисление и вывод индуктивного сопротивления, построение графика
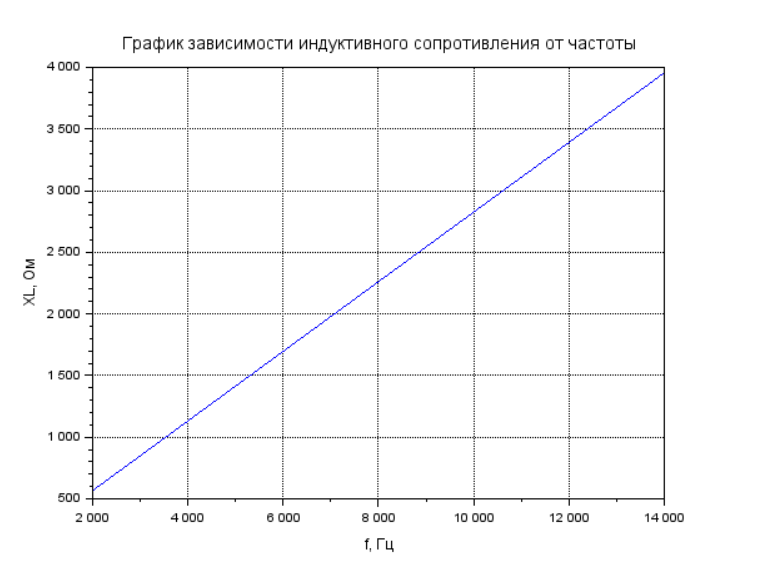
Рисунок 12 – График зависимости индуктивного сопротивления от частоты

Рисунок 13 – Вычисление и вывод модуля напряжения на катушке, построение графика
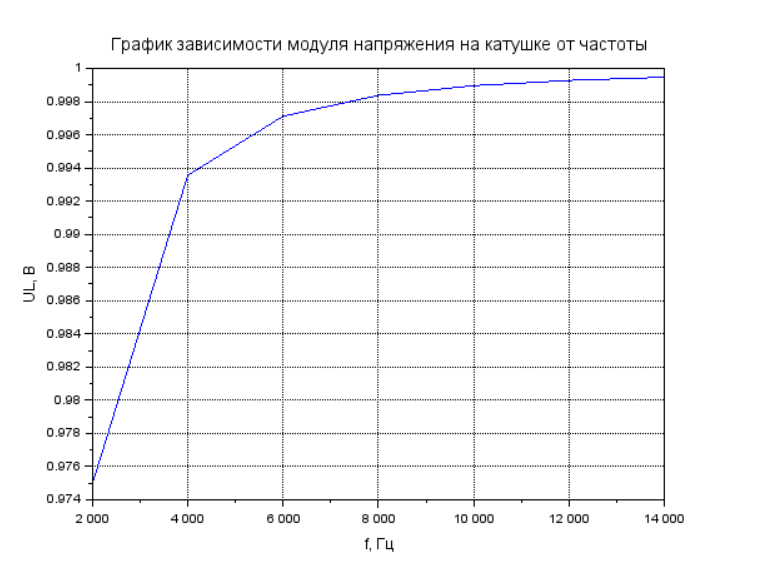
Рисунок 14 – График зависимости модуля напряжения на катушке от частоты

Рисунок 15 – Вычисление граничной частоты и отношения частоты к граничной частоте для каждого случая
2 Экспериментальный расчёт
В программе Micro-Cap воссоздадим схему цепи, построим графики функций и найдём искомые значения, чтобы сравнить их с предварительными расчётами.
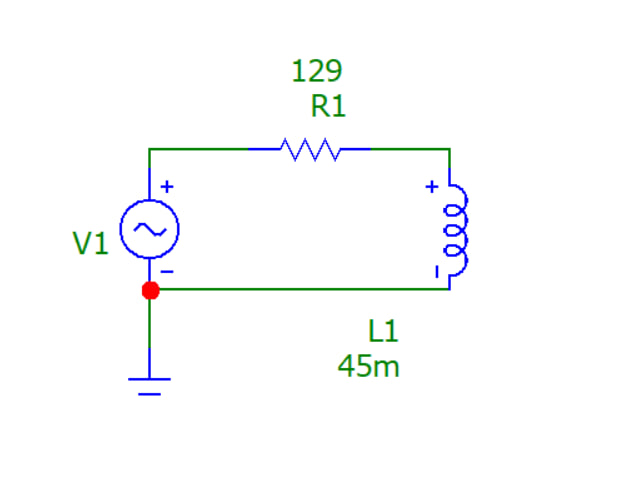
Рисунок 16 – Схема цепи
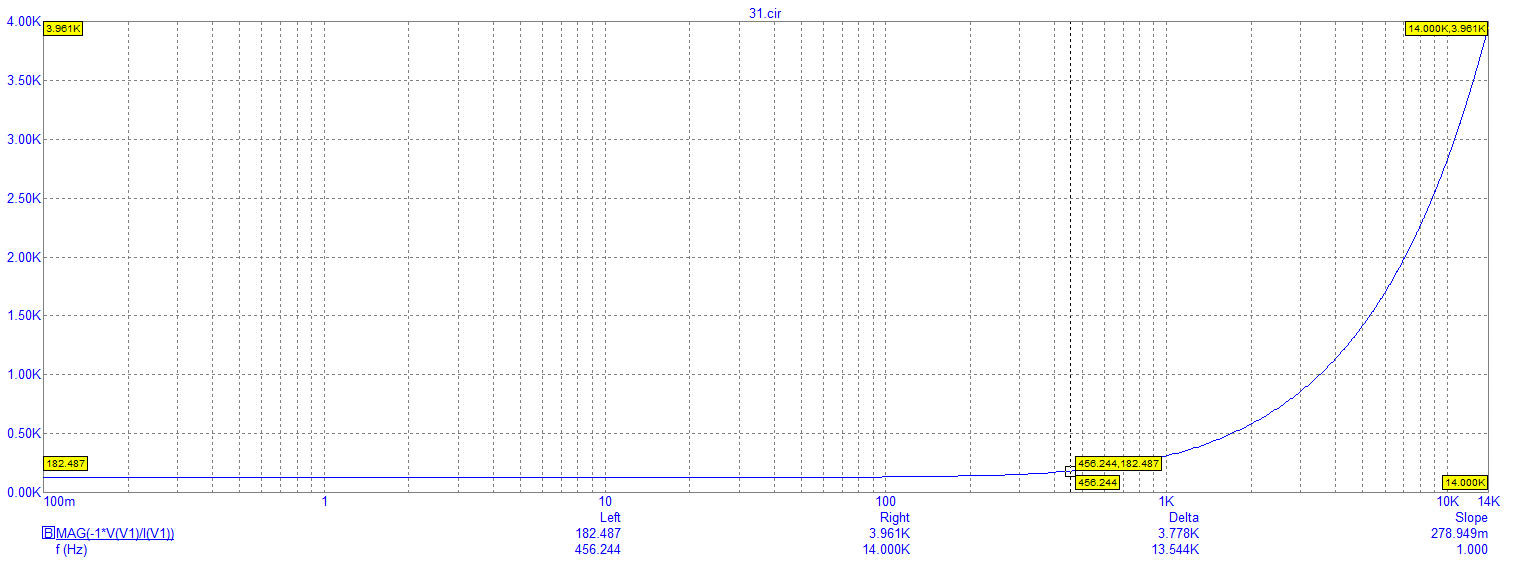
Рисунок 17 – Экспериментально полученный график зависимости модуля входного сопротивления от частоты
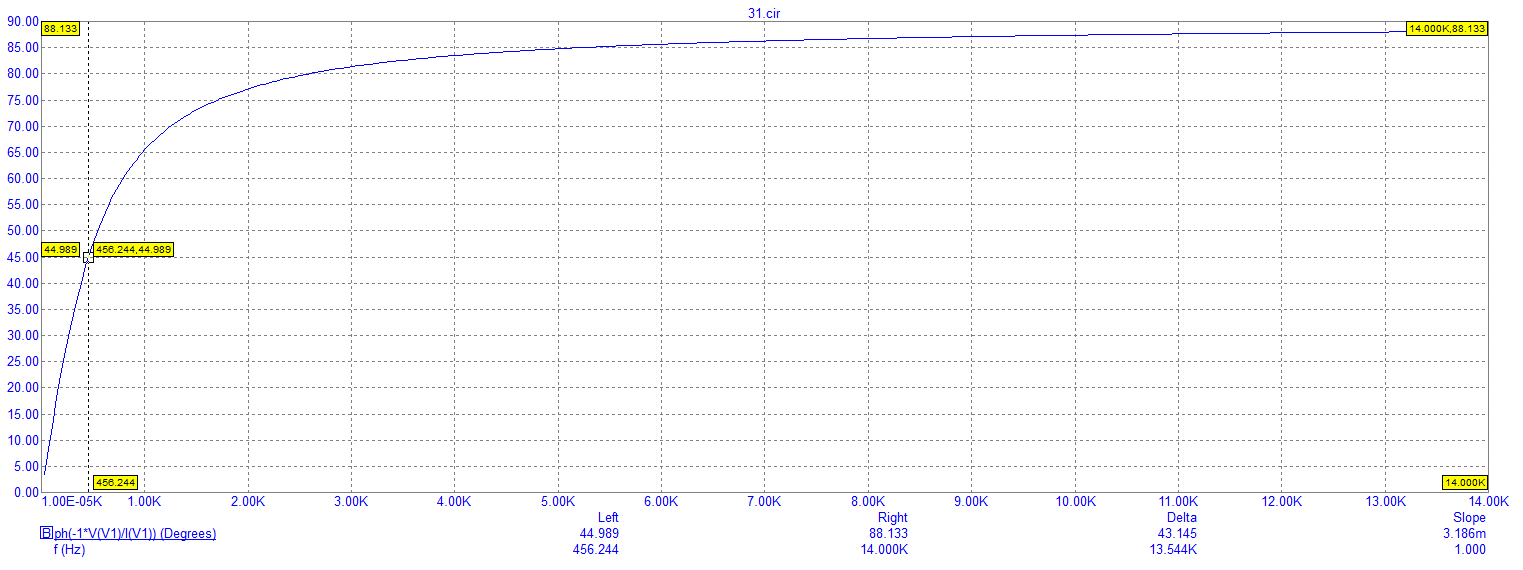
Рисунок 18 – Экспериментально полученный график зависимости фазы входного напряжения от частоты
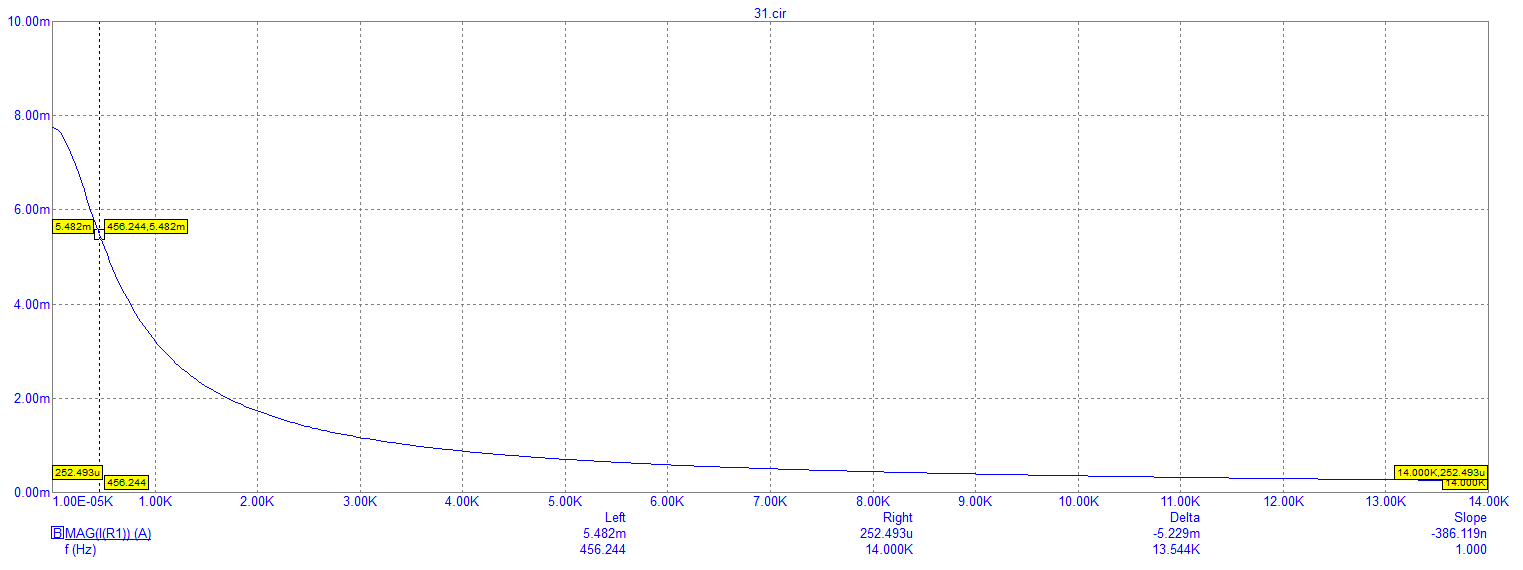
Рисунок 19 – Экспериментально полученный график зависимости модуля тока от частоты
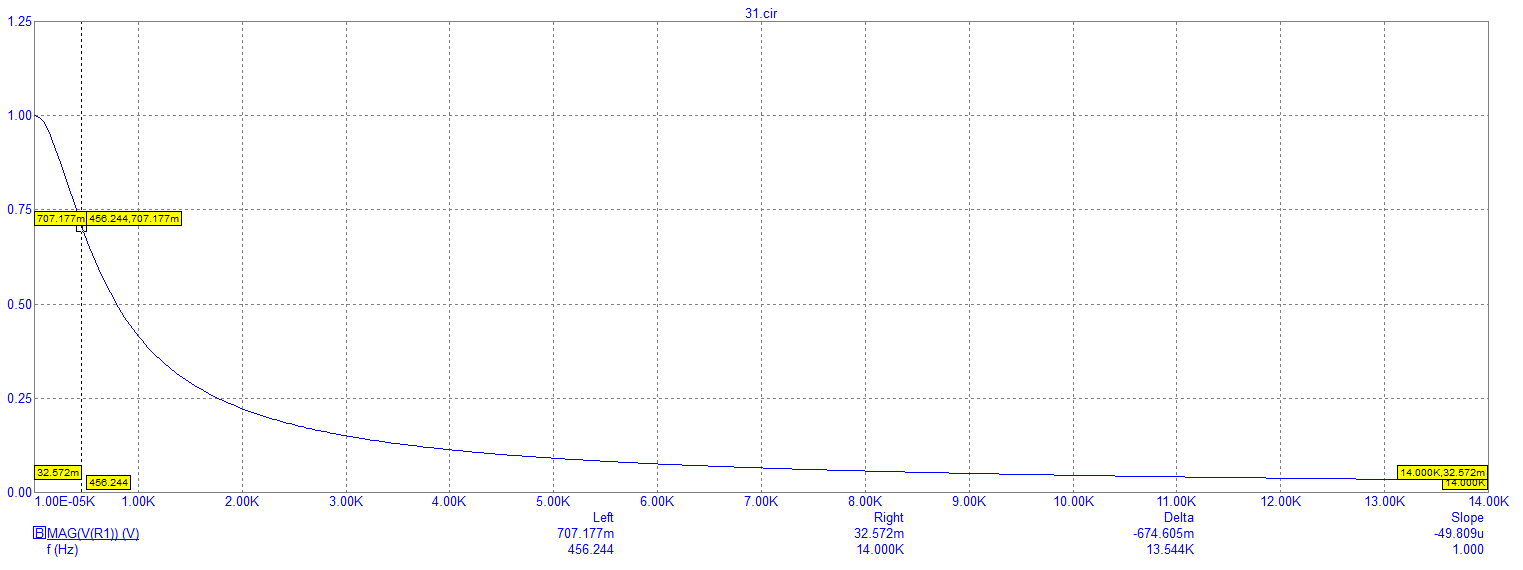
Рисунок 20 – Экспериментально полученный график зависимости модуля напряжения на резисторе от частоты
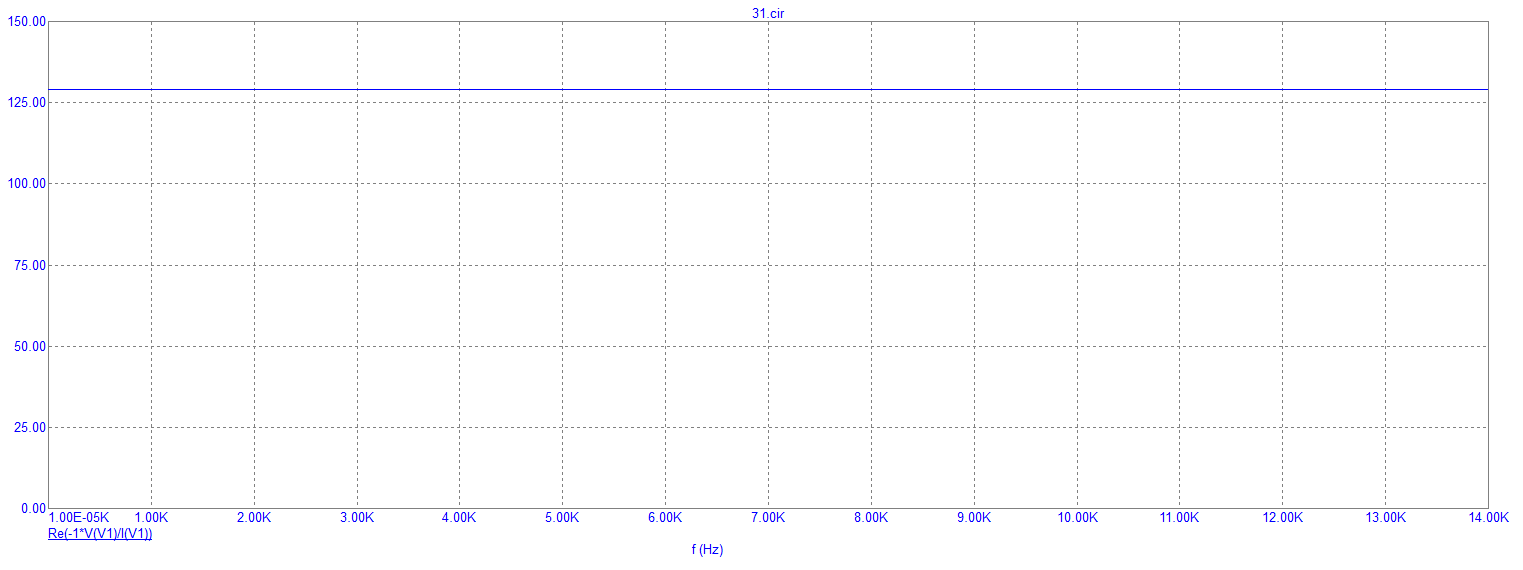
Рисунок 21 – Экспериментально полученный график зависимости резистивного сопротивления от частоты
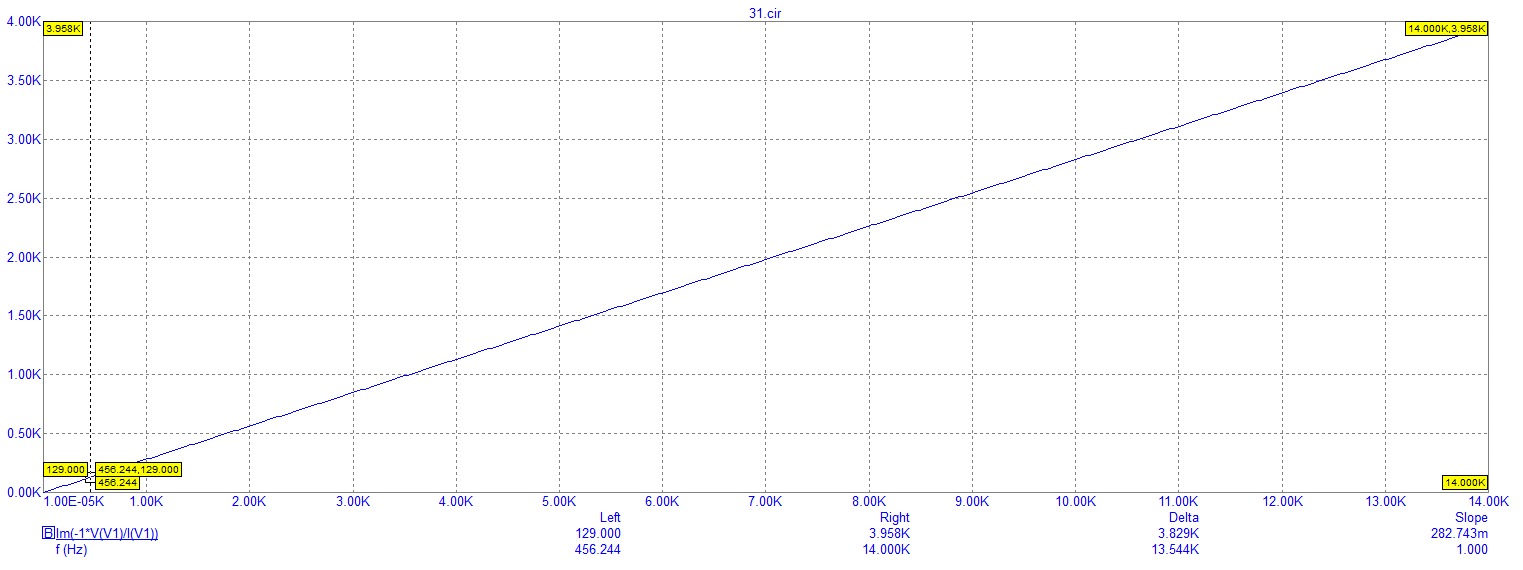
Рисунок 22 – Экспериментально полученный график зависимости индуктивного сопротивления от частоты
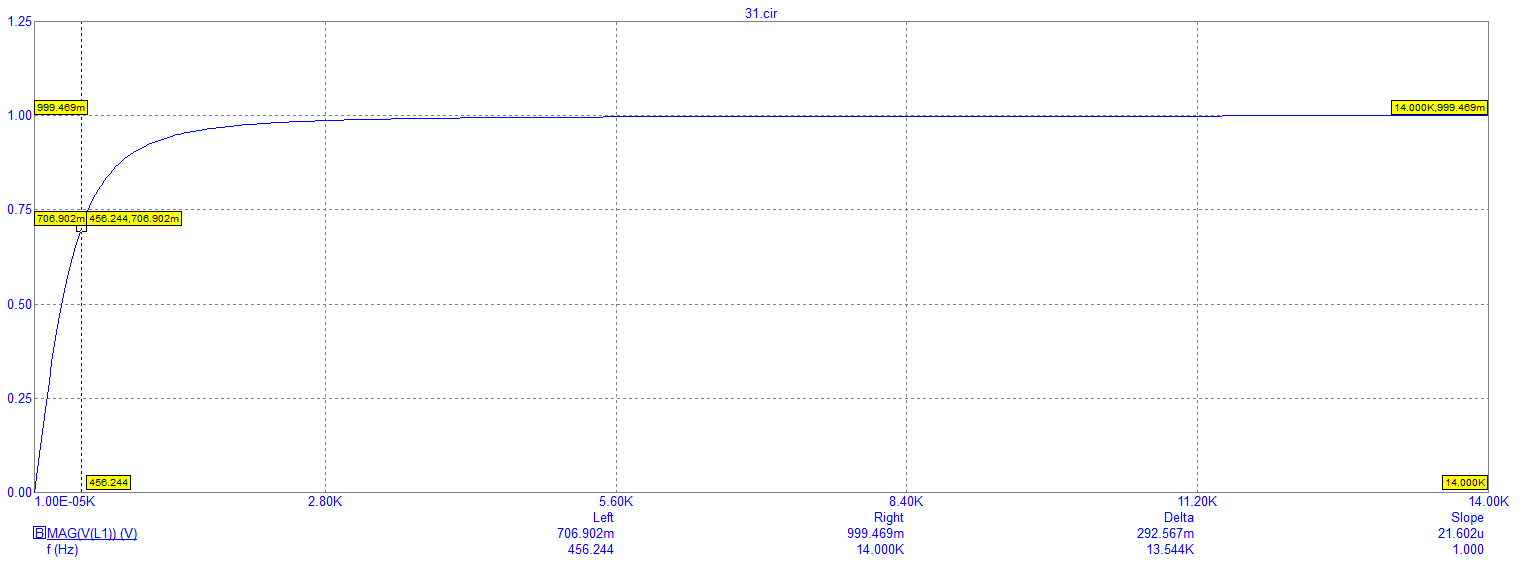
Рисунок 23 – Экспериментально полученный график зависимости модуля напряжения на катушке от частоты
Все значения, найденные по точкам на графиках, внесём в единую таблицу вместе с результатами предварительного расчёта (таблица 1).
Таблица 1 – Полученные данные
По предварительному расчёту |
|||||||||||||
f. кГц |
f/ |
Ом |
Ом |
град. |
I, мA |
В |
мВ |
||||||
2 |
4.384 |
565.49 |
580.01 |
77.149 |
1.724 |
0.222 |
0.975 |
||||||
4 |
8.767 |
1130.97 |
1138.3 |
83.493 |
0.878 |
0.113 |
0.994 |
||||||
6 |
13.151 |
1696.46 |
1701.36 |
85.652 |
0.588 |
0.076 |
0.997 |
||||||
8 |
17.534 |
2261.95 |
2265.62 |
86.736 |
0.441 |
0.057 |
0.998 |
||||||
10 |
21.918 |
2827.43 |
2830.37 |
87.388 |
0.353 |
0.046 |
0.999 |
||||||
12 |
26.302 |
3392.92 |
3395.37 |
87.823 |
0.295 |
0.038 |
0.999 |
||||||
14 |
30.685 |
3958.41 |
3960.51 |
88.133 |
0.252 |
0.033 |
0.999 |
||||||
Получено экспериментально |
|||||||||||||
f. кГц |
, Ом |
, Ом |
, град. |
I, мA |
, В |
, мВ |
|||||||
2 |
565 |
580 |
77.149 |
1,724 |
0,222 |
0,974 |
|||||||
4 |
1131 |
1138 |
83.493 |
0,878 |
0,113 |
0,994 |
|||||||
6 |
1696 |
1701 |
85.652 |
0,588 |
0,076 |
0,997 |
|||||||
8 |
2262 |
2266 |
86.736 |
0,441 |
0,057 |
0,998 |
|||||||
10 |
2827 |
2830 |
87.338 |
0,353 |
0,046 |
0,999 |
|||||||
12 |
3393 |
3395 |
87.823 |
0,295 |
0,038 |
0,999 |
|||||||
14 |
3958 |
3961 |
88.133 |
0,252 |
0,033 |
0,999 |
|||||||
Выводы
В данной работе с помощью программы Micro-Cap мы исследовали входные АЧХ и ФЧХ RL-цепи, сравнили АЧХ и ФЧХ, полученные с помощью программы MicroCap с аналогичными характеристиками, полученными расчетным путем.
Значения и графики, полученные в ходе эксперимента в Micro-Cap, совпадают с данными, полученными в ходе предварительного расчёта в программе Scilab. Это подтверждает корректность проведённого эксперимента и расчётов.
Вопросы для самопроверки
Какая частота называется граничной для RL-цепи?
Граничной частотой fгр называется частота, при которой действительная и мнимая части комплексного входного сопротивления равны.
Каково значение модуля входного сопротивления RL-цепи на граничной частоте?
На граничной частоте действительная и
мнимая части входного сопротивления
равны (в чём несложно убедиться, ведь
=
ωL = 2πfL
= 2*3.14*456.244*0.045=129 Ом), следовательно, модуль
числа
=
 =
=
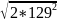 = 129*
= 129* = 182.43 Ом.
= 182.43 Ом.
Также на рисунке 17 отмечено это же значение для граничной частоты:
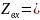 182.43 Ом.
182.43 Ом.
Каково значение аргумента входного сопротивления RL-цепи на граничной частоте?
Т.к.
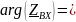
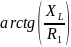 ,
а на граничной частоте
,
а на граничной частоте
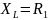 ,
следовательно,
,
следовательно,


По графику на рисунке 18: 45 град.
К чему стремится модуль тока RL-цепи при увеличении частоты?
Стремится к 0, так как он обратно пропорционален модулю входного сопротивления (по формуле ), а модуль входного сопротивления зависит от частоты f.
Это также видно на графике на рисунке 19.
Чему равен модуль входного сопротивления RL-цепи при частоте, равной нулю?
При f = 0 обнуляется мнимая
часть (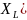 в формуле
в формуле
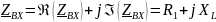 ,
следовательно, модуль входного
сопротивления
,
следовательно, модуль входного
сопротивления
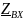 стремится к
= 129 Ом.
стремится к
= 129 Ом.

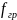
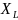 ,
,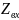 ,
,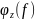 ,
,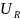 ,
,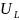 ,
,