
Лабы (Мосичев) / Лабораторная работа №30
.docxМинистерство цифрового развития, связи и массовых коммуникаций российской федерации
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
(МТУСИ)
Кафедра теории электрических цепей
Лабораторная работа №30
по дисциплине
«Электротехника»
на тему
Моделирование на ЭВМ переходных процессов в цепях первого порядка
Выполнил: студент группы БББ0000 факультета ИТ Фамилия И.О.
Проверил: к.т.н. Мосичев А.В.
Москва 2023г.
Цель работы:
С помощью машинного эксперимента исследовать переходные процессы в цепях первого порядка.
Исходные данные:
С1 = 0,25 мкФ = 0,25 ∙ 10-6 Ф – ёмкость конденсатора;
 =
20,40,80,160,320,640,1280,2560,5120 Ом – сопротивление
резистора;
=
20,40,80,160,320,640,1280,2560,5120 Ом – сопротивление
резистора;
L1 = 45 мГн = 45 ∙ 10-3 Гн – индуктивность катушки;
Для неразветвленной RC-цепи на постоянном напряжении:
E1 = 1 В; R1
= 160 Ом; C1 = 0,25 мкФ; t
 [0; 3τRC];
[0; 3τRC];
Для неразветвленной RL-цепи на постоянном напряжении:
E1 = 1 В; R1 = 160 Ом; L1 = 45 мГн; t [0; 3τRL];
Расчётные формулы:
τRC = R * C – постоянная времени RС-цепи;
τRL
=
 – постоянная времени RL-цепи;
– постоянная времени RL-цепи;
 (t) =
(t) =

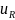 (t) =
(t) =
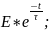
 (t) =
(t) =

i(t) =
 .
.
Предварительный расчёт
Проведём расчёт и построим графики в программе Scilab.

Рисунок 1 – Расчет постоянной времени для неразветвленной RC-цепи

Рисунок 2 – Расчет постоянной времени для неразветвленной RL-цепи
 Рисунок
3 – Расчёт временных зависимостей тока,
а также напряжения на резисторе и
конденсаторе в неразветвленной RC-цепи.
Рисунок
3 – Расчёт временных зависимостей тока,
а также напряжения на резисторе и
конденсаторе в неразветвленной RC-цепи.

Рисунок 4 – Графики зависимостей напряжения на конденсаторе и резисторе от времени

Рисунок 5 – График зависимости тока в RC-цепи от времени

Рисунок 6 – Расчёт временных зависимостей
тока, а также напряжения на резисторе
и катушке в неразветвленной RL-цепи.
Рисунок 7 – Графики зависимостей напряжения на катушке и резисторе от времени

Рисунок 8 – График зависимости тока в RL-цепи от времени
2 Экспериментальный расчёт
В программе Micro-Cap воссоздадим схемы цепей, построим графики функций и найдём искомые значения, чтобы сравнить их с предварительными расчётами.

Рисунок 9 – Схема цепи №1
U,
В
t,
мкc
I,
мА

t,
мкc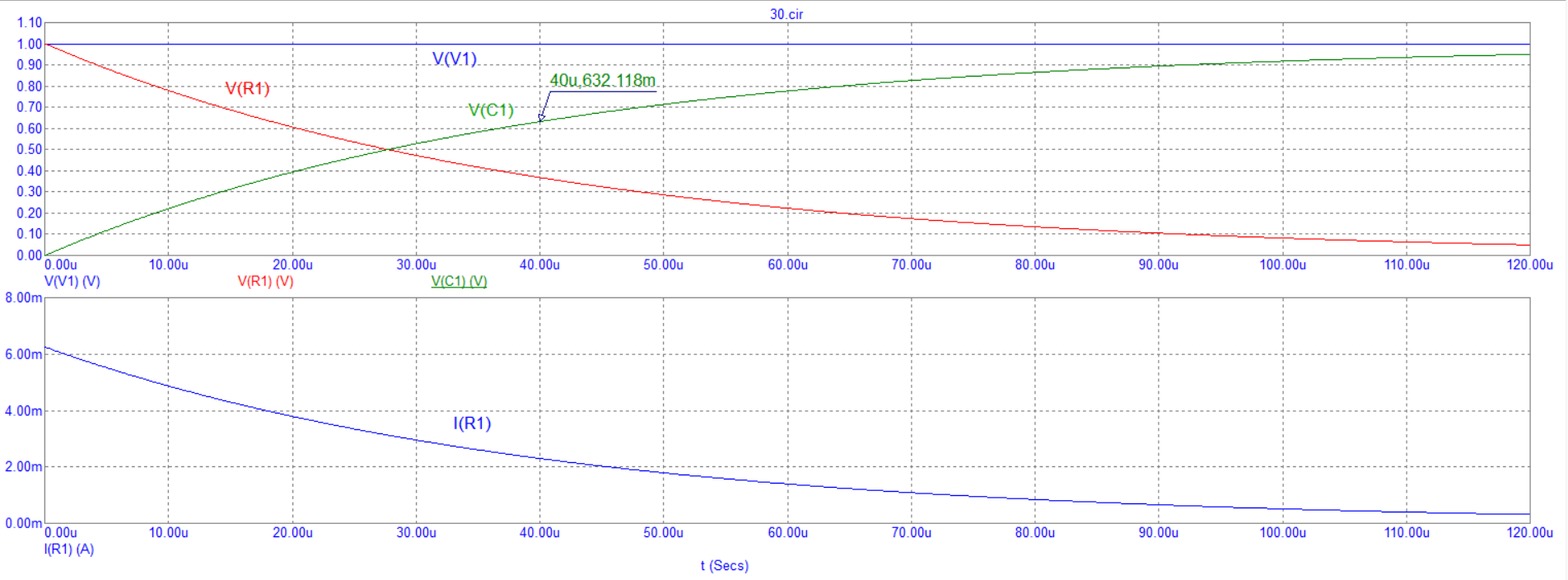
Рисунок 10 – Экспериментально полученные графики зависимости тока, напряжения на резисторе, напряжения на катушке и напряжения источника от времени для RC-цепи

Рисунок 11 – Схема цепи №2
U,
В
t,
мкc
t,
мкc
I,
мА
Рисунок 12 – Экспериментально полученные графики зависимости тока, напряжения на резисторе, напряжения на катушке и напряжения источника от времени для RL-цепи
Все значения, полученные экспериментально (а также значения предварительного расчёта) занесём в таблицу 1.
Таблица 1 – Полученные результаты
По предварительному расчету (C1 = 0,25 мкФ, L1 = 45 мГн) |
|||||||||
R1, Ом |
20 |
40 |
80 |
160 |
320 |
640 |
1280 |
2560 |
5120 |
τRC, мкс |
5 |
10 |
20 |
40 |
80 |
160 |
320 |
640 |
1280 |
τRL, мкс |
2250 |
1125 |
563 |
281 |
141 |
70 |
35 |
18 |
9 |
По экспериментальным данным |
|||||||||
τRC, мкс |
5 |
10 |
20 |
40 |
80 |
160 |
320 |
640 |
1280 |
τRL, мкс |
2250 |
1125 |
563 |
281 |
141 |
70 |
35 |
18 |
9 |
Выводы
В данной работе с помощью программы Micro-Cap мы исследовали переходные процессы в цепях первого порядка, а затем сравнили характеристики, полученные с помощью программы Micro-Cap, с аналогичными характеристиками, полученными расчетным путем.
Значения и графики, полученные в ходе эксперимента в Micro-Cap, совпадают с данными, полученными в ходе предварительного расчёта в программе Scilab. Это подтверждает корректность проведённого эксперимента и расчётов.
Вопросы для самопроверки
Что называется переходным процессом? Приведите пример.
Переходный процесс – это процесс перехода цепи от одного установившегося режима к другому. Например, при включении, переключении, изменении параметров цепи – так как это обусловлено коммутацией в цепи.
Какие цепи называют цепями первого порядка? Приведите пример.
Порядок электрической цепи определяется числом реактивных элементов. Цепь первого порядка (n = 1) включает один реактивный элемент – индуктивность или ёмкость и любое число резистивных элементов и независимых источников питания. Примеры – RL и RC-цепи.
Какой режим называется установившемся? Приведите пример.
Режим называется установившимся, если параметры цепи либо постоянны во времени, либо постоянны по амплитуде тока и напряжения. Как, например, в случае цепи, ещё не подключённой к источнику электросигнала, – то есть цепи, в которой ещё нет токов.
Какой физический смысл постоянной времени тока?
Физически постоянная времени определяет время, в течение которого свободная составляющая тока или свободная составляющая напряжения в цепи уменьшается в e раз:
Uсв(τ)
= Umaxe-1=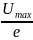 ;
;
Она служит практической мерой продолжительности переходного процесса, так как теоретически переходный процесс длится бесконечно долго, и позволяет сравнивать различные цепи в отношении времени стационарного режима.
Как по графику рассчитать постоянную времени цепи? Приведите пример.
Необходимо найти время, равное постоянной времени, то есть t = τ. тогда, например, формула для RC-цепи:
![]() ,
т.к. t
= τ, следовательно,
,
т.к. t
= τ, следовательно,![]()
По ней мы можем найти значение Uc, которое будет равно ≈ 0,632В, чему соответствует постоянная времени τ = 40 мкс (при R1 = 160 Ом)
Практические задания и задачи к промежуточному контролю
Сформулируйте два закона коммутации.
Первый закон коммутации: В начальный момент времени после коммутации ток в уединенной индуктивности не может измениться скачком и сохраняет такое же значение, как и непосредственно перед коммутацией.
iL(-0) = iL(+0);
Второй закон коммутации: В начальный момент времени после коммутации напряжение на уединенной емкости не может измениться скачком и сохраняет такое же значение, как и непосредственно перед коммутацией.
uC(-0) = uC(+0);
При каких условиях говорят, что в цепи имеют место нулевые начальные значения? Что в этом случае представляют собой катушка и конденсатор в начальный момент?
Если в момент, непосредственно предшествующий коммутации, токи в индуктивностях электрической цепи и напряжения на конденсаторах были равны нулю (то есть iL(-0) = 0 и uC(-0) = 0),
то говорят, что в цепи имеют место нулевые начальные условия.
При нулевых начальных условиях в начальный момент времени конденсатор представляет собой короткое замыкание, а катушка индуктивности – обрыв (холостой ход).
Когда переходный процесс принято считать закончившимся?
Переходный процесс теоретически длится бесконечно долго, но его принято считать закончившимся по истечении времени ty = 3τ.
Это время называется временем установления.
Докажите, что скачок тока в индуктивности в первый момент после коммутации невозможен.
Предположим, что ток iL(t) действительно изменяется скачком, тогда:
 ;
;
 ,
,
Из этого следует, что требуемая мощность:
P =
 L
L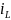 (t)
(t) =
=
 при t = 0
при t = 0
Следовательно, для этого требуется источник с бесконечно большой мощностью, что невозможно на практике.
Какие цепи называют цепями n-го порядка?
Переходные процессы в цепях описываются уравнениями на основе законов Кирхгофа для мгновенных значений напряжения и тока. Для линейных цепей эти уравнения приводятся к линейным дифференциальным уравнениям вида:

Цепи, описываемые дифференциальным уравнением такого типа, называются цепями n-го порядка. Порядок цепи обычно равен числу реактивных элементов цепи.
Опишите классический метод расчёта переходных процессов.
Согласно этому методу, решение дифференциального уравнения (n-го порядка, представленного выше) необходимо искать в виде суммы двух слагаемых:
 ;
;
Где
 – свободная составляющая искомой
функции, т.е. общее решение однородного
дифференциального уравнения при f(t)
= 0;
– свободная составляющая искомой
функции, т.е. общее решение однородного
дифференциального уравнения при f(t)
= 0;
 – установившаяся составляющая, частное
решение исходного уравнения, представляет
собой вынужденный режим, задаваемый в
цепи внешними источниками.
– установившаяся составляющая, частное
решение исходного уравнения, представляет
собой вынужденный режим, задаваемый в
цепи внешними источниками.
Так как в цепи происходят потери энергии на резисторе R, свободная составляющая со временем затухает.
Как связаны между собой мгновенный ток и мгновенное напряжение на R-, L- и С- элементах цепи?
Для резистора R:
uR=RiR,
iR= ;
;
Для катушки индуктивности L:
uR=L ,
,
 ;
;
Для конденсатора C:
 ,
iC=C
,
iC=C ;
;
