
Лабы (Мосичев) / Лабораторная работа №16
.docxМинистерство цифрового развития, связи и массовых коммуникаций российской федерации
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
(МТУСИ)
Кафедра теории электрических цепей
Лабораторная работа №16
по дисциплине
«Электротехника»
на тему
Исследование на ЭВМ резонансных явлений в пассивном и активном последовательном колебательном контуре
Выполнил: студент группы БББ0000 факультета ИТ Фамилия И.О.
Проверил: к.т.н. Мосичев А.В.
Москва 2023г.
Цель работы:
С помощью программы Micro-Cap исследовать характеристики одиночного последовательного пассивного и активного колебательного контура при различных добротностях.
Исходные данные
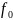 = 4,8 кГц = 4800 Гц – резонансная частота;
= 4,8 кГц = 4800 Гц – резонансная частота;
С = 38 нФ = 38 ∙ 10-9 Ф – ёмкость конденсатора;
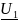 = 1В – комплексное напряжение контура;
= 1В – комплексное напряжение контура;
f ∈ [2; 8] кГц – частота;
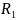 = 160 Ом – сопротивление резистора №1;
= 160 Ом – сопротивление резистора №1;
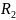 = 640 Ом – сопротивление резистора №2;
= 640 Ом – сопротивление резистора №2;
Расчётные формулы
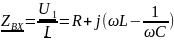 – комплексное входное сопротивление
контура;
– комплексное входное сопротивление
контура;
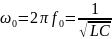 – резонансная частота контура;
– резонансная частота контура;
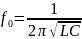 – резонансная частота;
– резонансная частота;
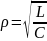 –
характеристическое
сопротивление;
–
характеристическое
сопротивление;
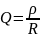 =
=
 –
добротность;
–
добротность;
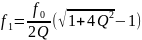 – нижняя
граничная частота;
– нижняя
граничная частота;
 – верхняя
граничная частота;
– верхняя
граничная частота;
П = f2 – f1 – абсолютная полоса пропускания;
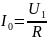 – модуль
входного тока при резонансе;
– модуль
входного тока при резонансе;
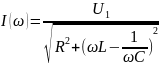 – резонансная
кривая тока при условии, что меняется
только частота источника напряжения.
– резонансная
кривая тока при условии, что меняется
только частота источника напряжения.
Для гиратора:
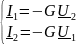 где G
– проводимость гиратора (коэффициент
гирации);
где G
– проводимость гиратора (коэффициент
гирации);
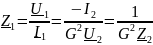 – входное сопротивление нагруженного
гиратора;
– входное сопротивление нагруженного
гиратора;
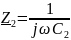 – выходное сопротивление гиратора;
– выходное сопротивление гиратора;
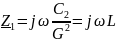 – входное сопротивление гиратора;
– входное сопротивление гиратора;
L
=
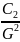 – эквивалентная индуктивность;
– эквивалентная индуктивность;
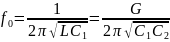 – резонансная частота;
– резонансная частота;
Предварительный расчёт
Проведём предварительный расчёт и построим графики в программе Scilab.
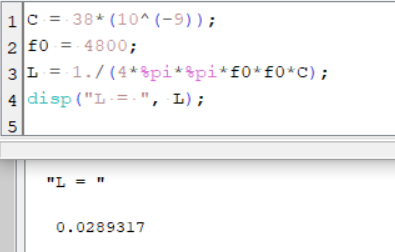
Рисунок 1 – Рассчёт величины индуктивности L
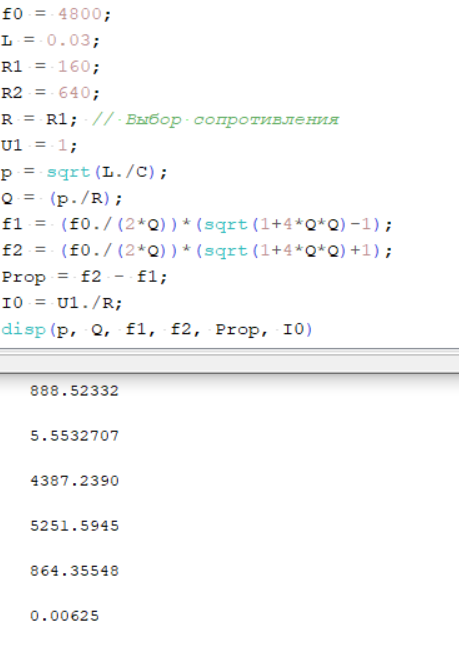
Рисунок 2 – Исходные данные, вычисление
и вывод искомых значений
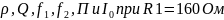
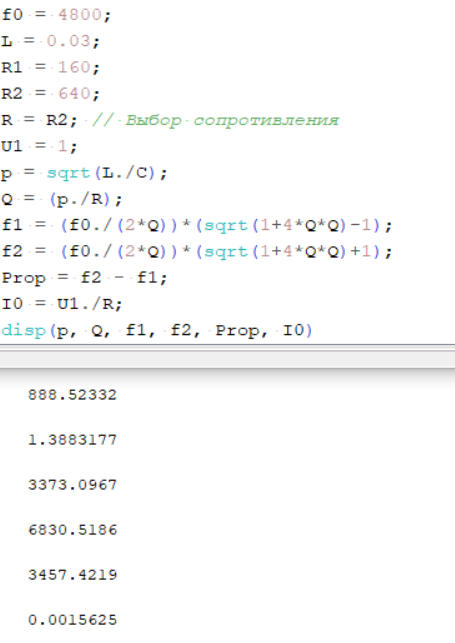
Рисунок 3 – Исходные данные, вычисление
и вывод искомых значений

Рисунок 4 – Построение графиков
зависимостей входного сопротивления
от частоты при
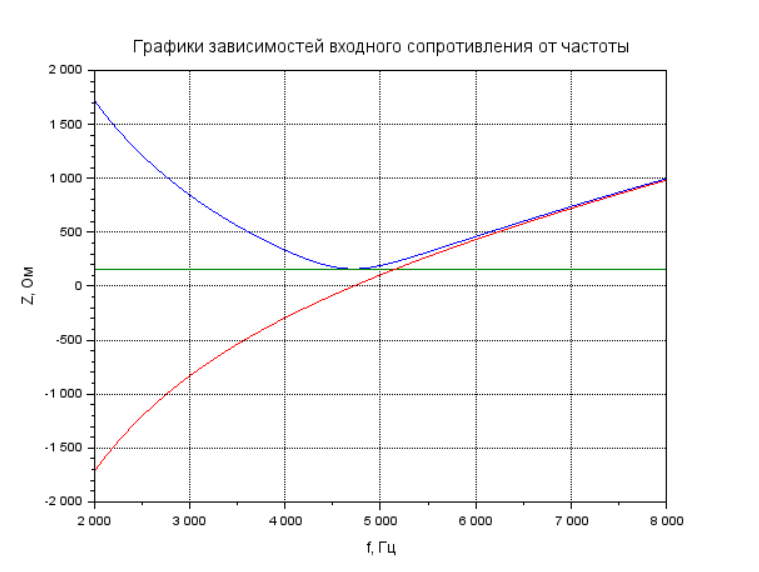
Рисунок 5 – Графики зависимостей входного сопротивления от частоты при
Рисунок 6 – Построение графиков
зависимостей входного сопротивления
от частоты
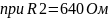

Рисунок 7 – Графики зависимостей входного сопротивления от частоты

Рисунок 8 – Построение графиков зависимостей фазы входного сопротивления от частоты при R1=160 и R2=640

Рисунок 9 – Графики зависимостей фазы входного сопротивления от частоты при R1=160 и R2=640

Рисунок 10 – Построение графиков зависимостей модуля входного тока от частоты при R1=160 и R2=640
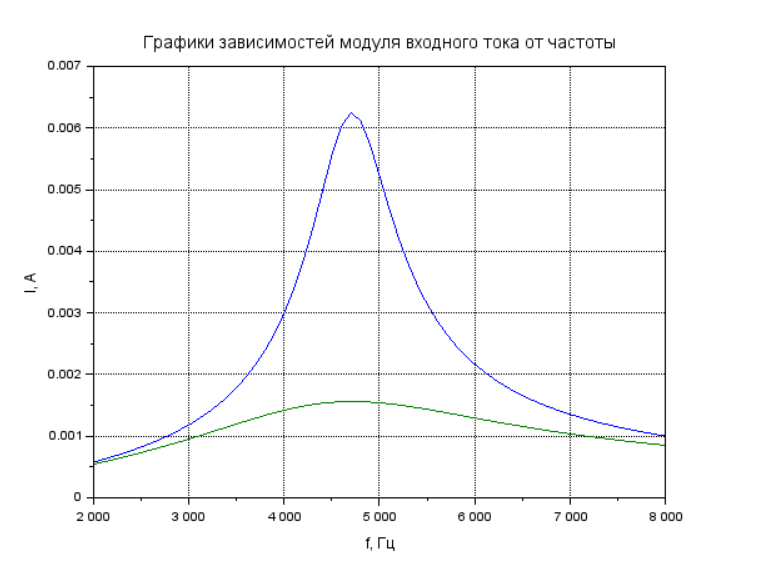
Рисунок 11 – Графики зависимостей модуля входного тока от частоты при R1=160 и R2=640
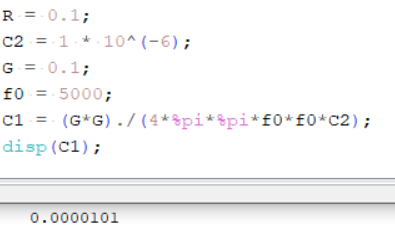
Рисунок 12 – Рассчёт значения ёмкости
 для гиратора
для гиратора
2 Экспериментальный расчёт
В программе Micro-Cap воссоздадим схемы цепей, построим графики функций и найдём искомые значения, чтобы сравнить их с предварительными расчётами.
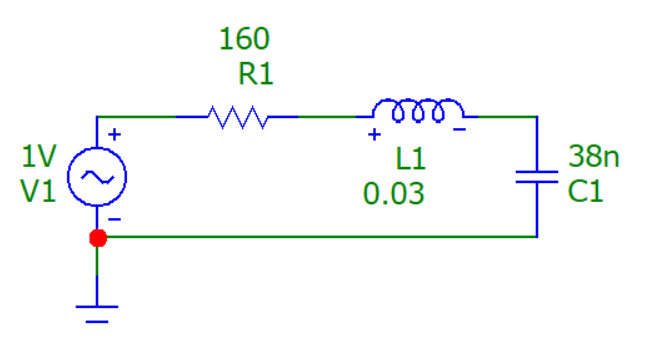
Рисунок 13 – Схема цепи №1
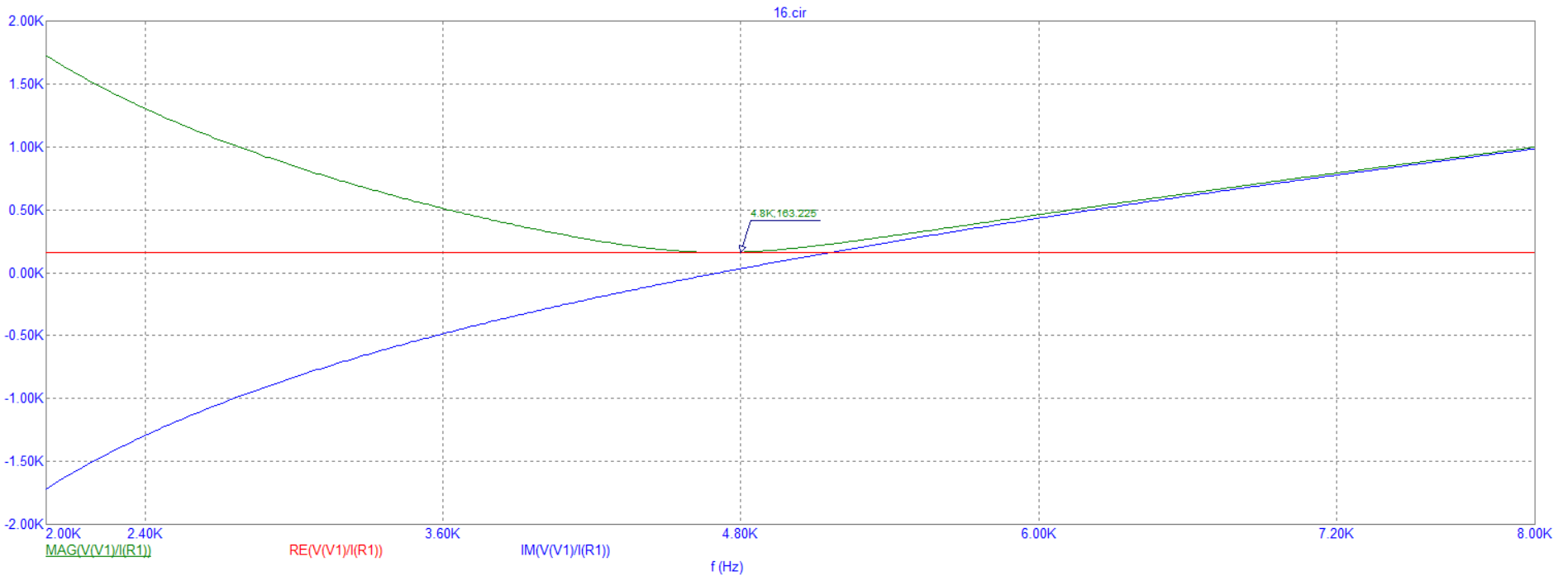
Рисунок 14 – Экспериментально полученные графики зависимостей входного сопротивления от частоты при
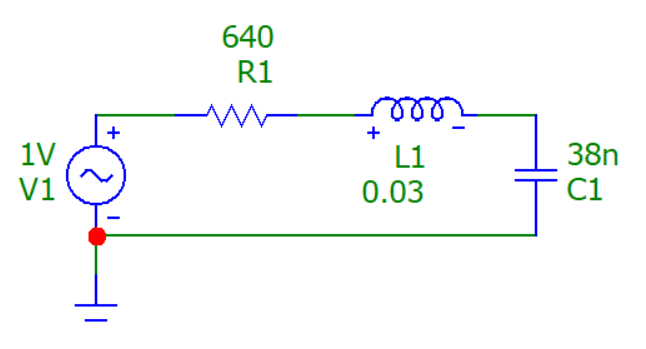
Рисунок 15 – Схема цепи №2 (изменённое значение R)
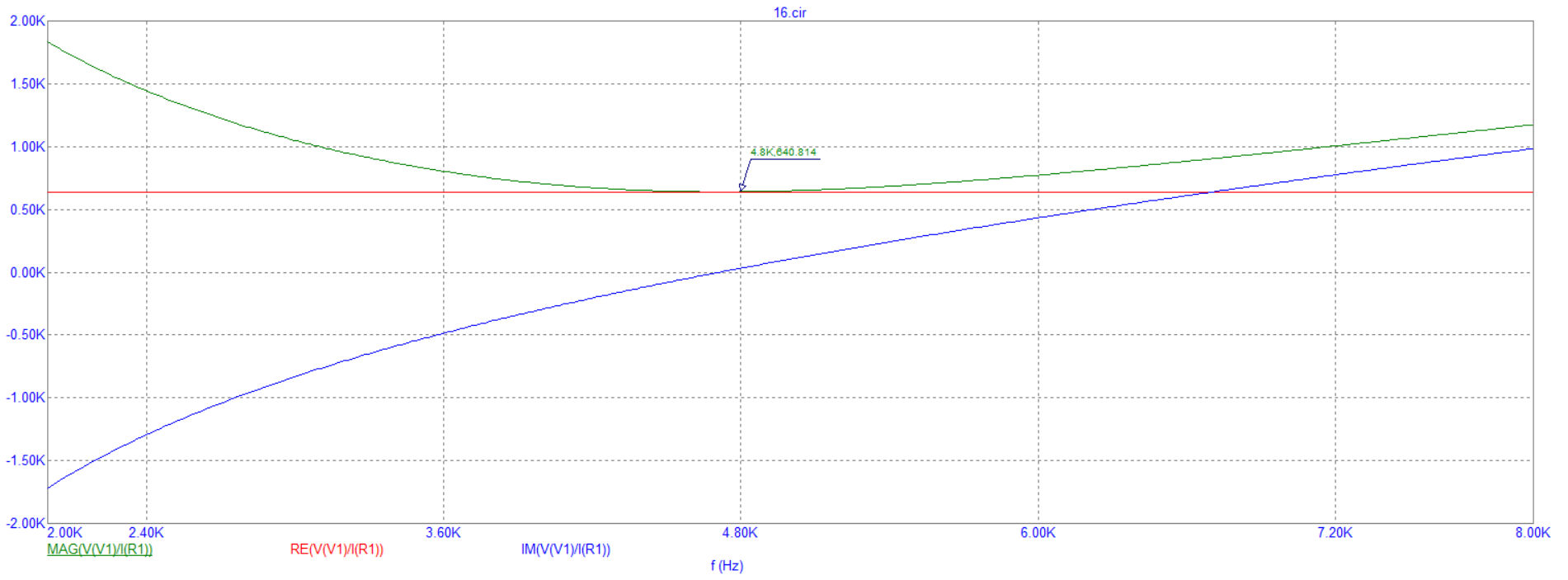
Рисунок 16 – Экспериментально полученные
графики зависимостей входного
сопротивления от частоты при
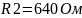
Рисунок 17 – Экспериментально полученные графики зависимостей фаз входного сопротивления от частоты при различных значениях R
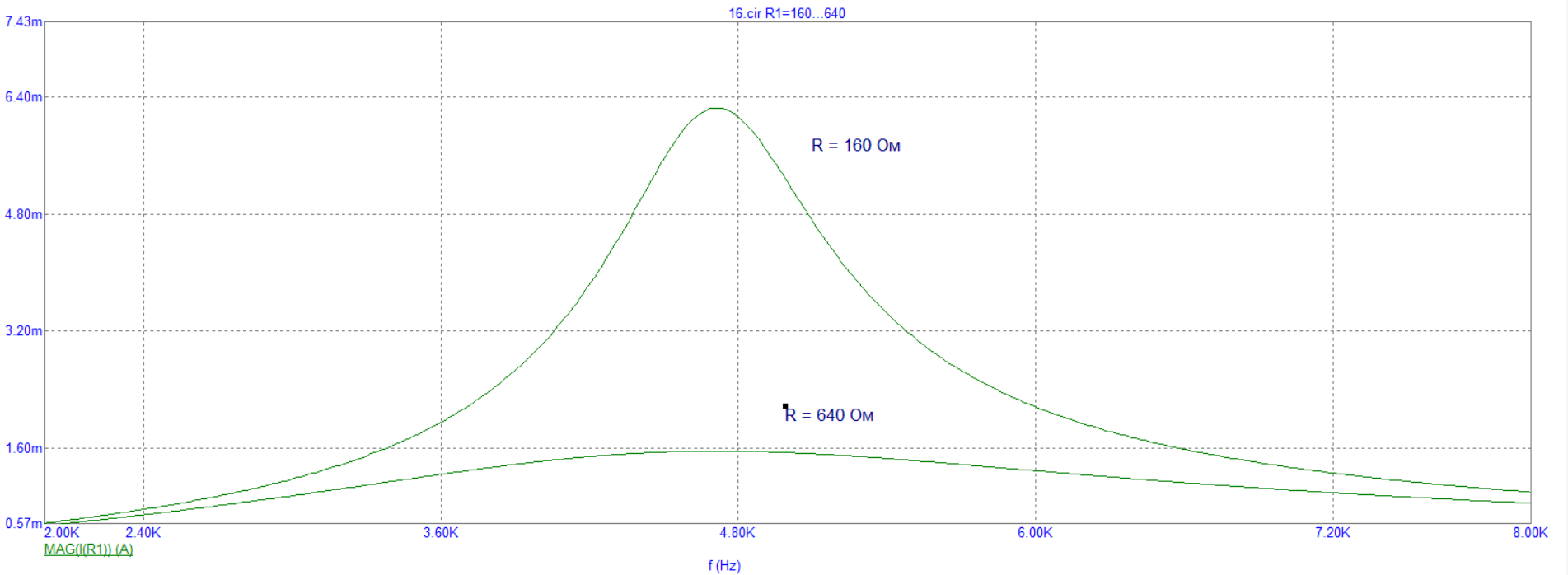
Рисунок 18 – Экспериментально полученные графики зависимостей фаз входного сопротивления от частоты при различных значениях R
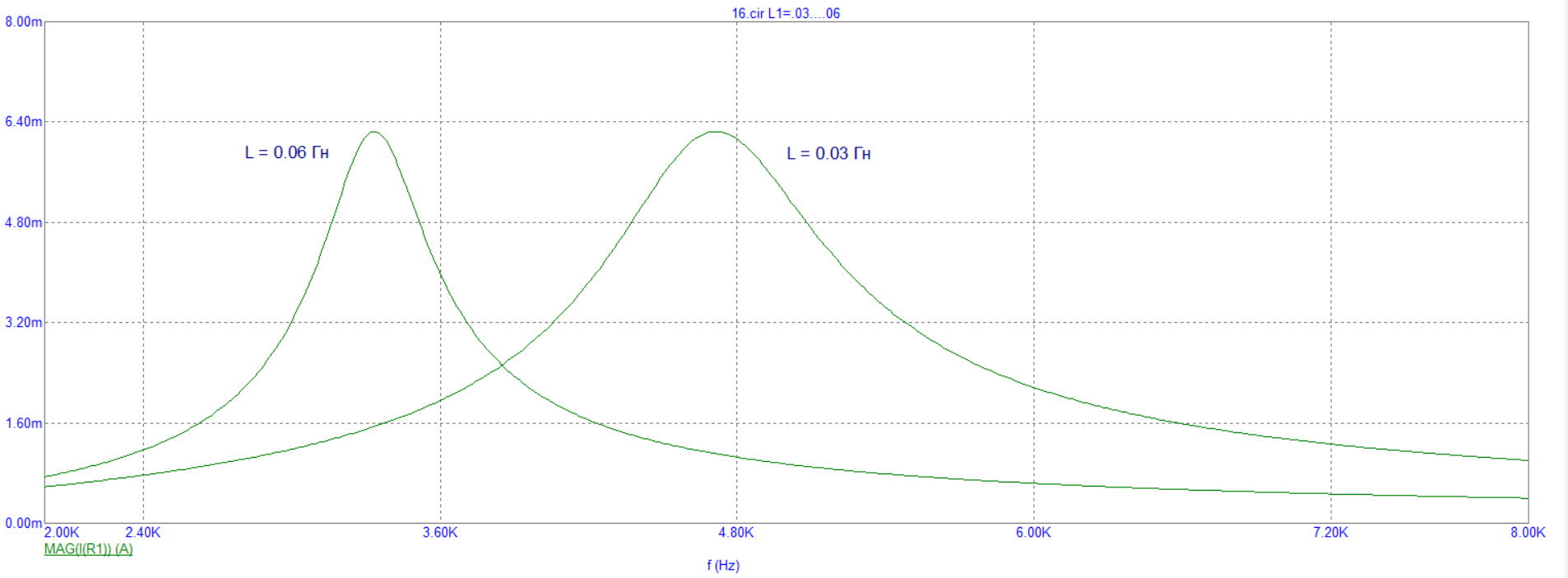
Рисунок 19 – Экспериментально полученные графики зависимостей фаз входного сопротивления от частоты при различных значениях L
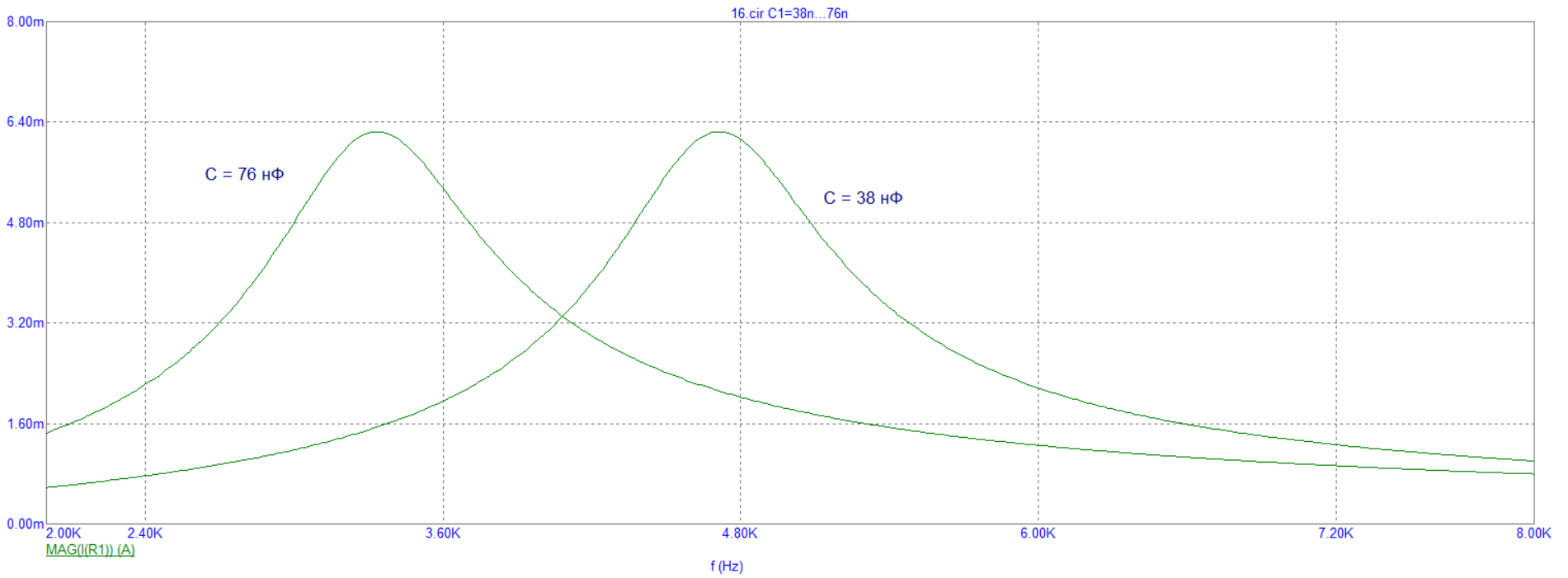
Рисунок 20 – Экспериментально полученные графики зависимостей фаз входного сопротивления от частоты при различных значениях C
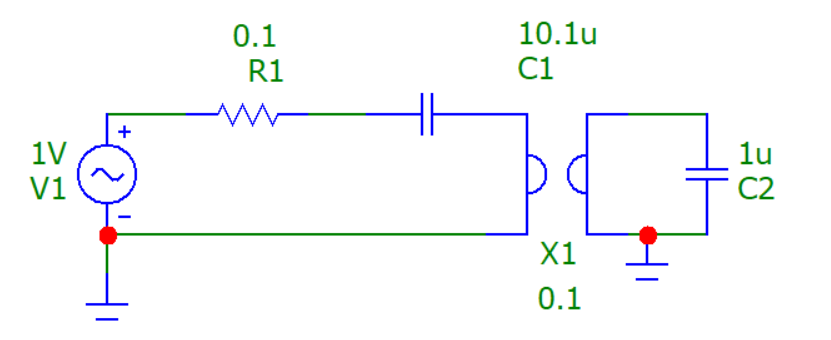
Рисунок 21 – Схема цепи №3 (Гиратор)
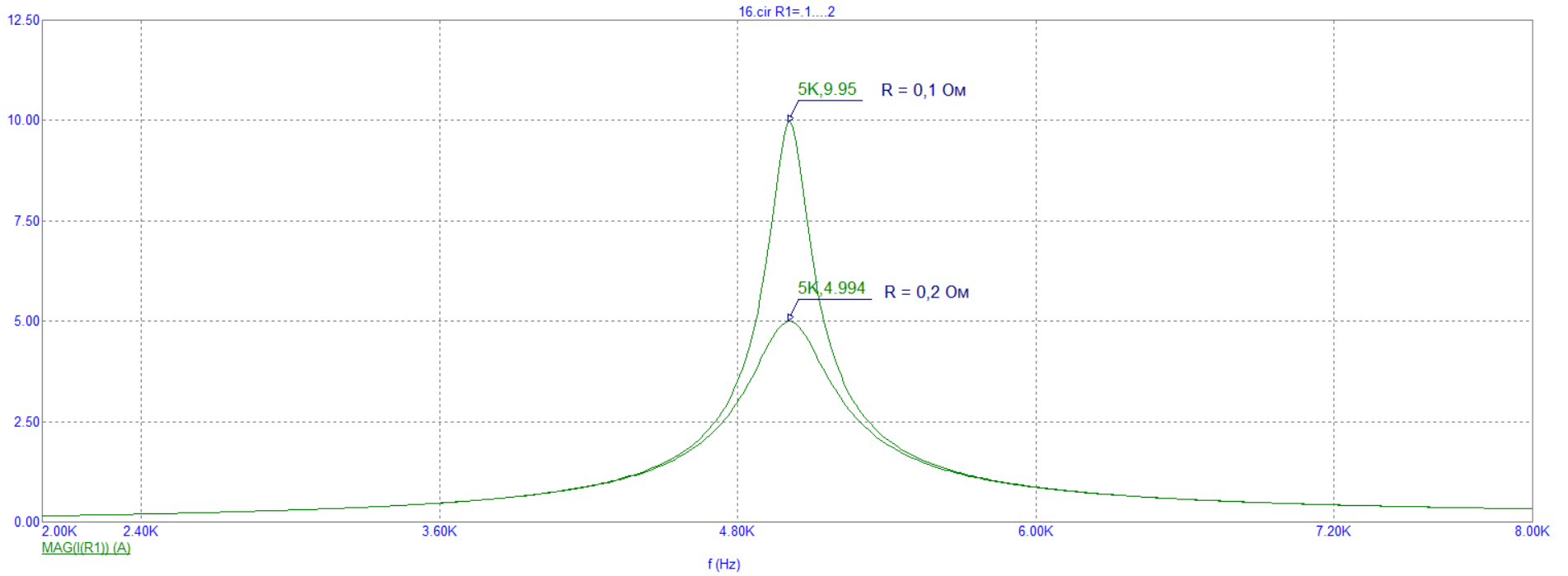
Рисунок 22 – Экспериментально полученные графики зависимостей модуля входного тока гиратора от частоты при различных значениях R
Все значения, полученные экспериментально (а также значения предварительного расчёта) занесём в таблицу 1.
Таблица 1 – Полученные результаты
По предварительному расчету U1 = 1 B, f0 = 4,8 кГц, С = 38 нФ, L = 0,03 Гн |
Получено экспериментально |
||||||||||||||
R, Ом |
|
Q |
f1, кГц |
f2, кГц |
П, кГц |
I0, А |
f0, кГц |
f0, кГц |
I0, А |
f1, кГц |
f2, кГц |
П, кГц |
Q |
||
160 |
888.52 |
5.55 |
4.39 |
5.25 |
0.86 |
0.00625 |
4.8 |
4,72 |
0.00625 |
4.3 |
5.2 |
0,9 |
5,24 |
||
640 |
888.52 |
1.39 |
3.37 |
6,83 |
3.46 |
0.00156 |
4.8 |
4,72 |
0,00155 |
3.3 |
6.75 |
3,45 |
1,37 |
||
Гиратор |
|||||||||||||||
По предварительному расчету U1 = 1 B, f0 = 5 кГц, С2 = 1 мкФ, G = 0,1 См |
Получено экспериментально |
||||||||||||||
R, Ом |
С1, мкФ |
f0, кГц |
|||||||||||||
0,1 |
10,1 |
5 |
|||||||||||||
Выводы
В данной работе с помощью программы Micro-Cap мы исследовали характеристики одиночного последовательного пассивного и активного колебательного контура при различных добротностях, а затем сравнили характеристики, полученные с помощью программы Micro-Cap, с аналогичными характеристиками, полученными расчетным путем.
Значения и графики, полученные в ходе эксперимента в Micro-Cap, совпадают с данными, полученными в ходе предварительного расчёта в программе Scilab. Это подтверждает корректность проведённого эксперимента и расчётов.
Вопросы для самопроверки
Почему резонанс в последовательном пассивном колебательном контуре называется резонансом напряжений?
Закон Ома для действующего значения тока в RLC-контуре:
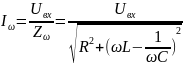 – функция имеет максимум при
– функция имеет максимум при
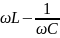 = 0, где
= 0, где
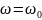 .
Таким образом, X=
.
Таким образом, X=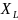 -
-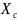 =0.
Так как элементы R L
C подключены последовательно
– по ним течёт один и тот же ток I,
при этом напряжение на конденсаторе
отстаёт от тока на 90º, а напряжение на
катушке – опережает ток на 90º. Таким
образом,
=0.
Так как элементы R L
C подключены последовательно
– по ним течёт один и тот же ток I,
при этом напряжение на конденсаторе
отстаёт от тока на 90º, а напряжение на
катушке – опережает ток на 90º. Таким
образом,
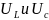 сдвинуты по фазе относительно друг
друга на 180º, то есть действуют напряжения
друг против друга. Поэтому это и называется
резонансом напряжений.
сдвинуты по фазе относительно друг
друга на 180º, то есть действуют напряжения
друг против друга. Поэтому это и называется
резонансом напряжений.
Как рассчитывается резонансная частота сложного пассивного колебательного контура, и как она рассчитывается для схем, содержащих гиратор?
Для сложного пассивного колебательного контура: ;
Для
схем с гиратором:
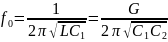
Что такое добротность последовательного пассивного колебательного контура?
Добротность
– это отношение характеристического
сопротивления к резистивному
;
она пропорциональна запасу электромагнитной
энергии в поле при резонансной частоте,
делённому на энергию выделяемого тепла
на сопротивлении R за
первый период T при
резонансной частоте: Q =
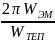 .
.
Добротность
также показывает, во сколько раз
напряжение на индуктивности или на
ёмкости больше входного: Q
=
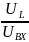 =
=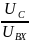 .
.
Также она задаётся отношением резонансной частоты к абсолютной полосе пропускания: Q =
Что такое полоса пропускания последовательного пассивного колебательного контура? Какие существуют способы расчета полосы пропускания?
Полосой пропускания последовательного
пассивного колебательного контура
называется диапазон частот, на которых
передаточная функция составляет 1/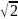 = 0,707 от передаточной функции на резонансной
частоте. Границы полосы пропускания –
те частоты, при которых средняя мощность,
поглощаемая контуром, вдвое меньше
средней мощности, поглощаемой при
резонансе:
= 0,707 от передаточной функции на резонансной
частоте. Границы полосы пропускания –
те частоты, при которых средняя мощность,
поглощаемая контуром, вдвое меньше
средней мощности, поглощаемой при
резонансе:
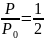 .
.
Передача сигнала должна осуществляться в данной полосе частот – для предотвращения искажений.
Рассчитывается: по разности П = f2 – f1, по графику АЧХ.
Выведите уравнения, с помощью которых рассчитывают входные АЧХ и ФЧХ последовательного пассивного колебательного контура.
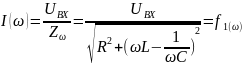 – АЧХ
(а также первая резонансная кривая),
достигает максимума при резонансной
частоте
– АЧХ
(а также первая резонансная кривая),
достигает максимума при резонансной
частоте
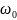 .
.
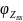 = arctg(
= arctg(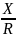 )
= arctg(
)
= arctg(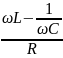 )
= Ф(
)
= Ф(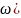 – ФЧХ, при резонансной частоте
= 0.
– ФЧХ, при резонансной частоте
= 0.

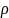 ,
Ом
,
Ом