Лекция 10

Основные понятия и законы, которые должны быть освоены в ходе лекции: дифракция, принцип Гюйгенса – Френеля, зоны Френеля и их свойства; расчет амплитуды и интенсивности световой волны в точке наблюдения; дифракция Френеля на отверстии и на диске; зонные пластинки.

3.3. Дифракция

Дифракция света – комплекс явлений, наблюдаемых при распространении световой волны в среде с резкими оптическими неоднородностями и связанных с нарушением законов геометрической оптики: в результате дифракции свет отклоняется от прямолинейного распространения и, огибая препятствия, оказывается в области геометрической тени. При этом наблюдается пространственное перераспределение интенсивности световой волны – интерференция. Для наблюдения дифракции необходимо, чтобы размеры оптических неоднородностей (преград, экранов, щелей) были соизмеримы с длиной световой волны.

Для объяснения дифракции используют принцип Гюйгенса – Френеля (сформулирован в 1815 г.), в соответствии с которым каждая точка волнового фронта является источником вторичных волн, когерентных между собой. Огибающая этих волн определяет положение волнового фронта в следующий момент времени. В случае распространения света в однородной изотропной среде, вторичные когерентные волны являются сферическими.

Вторичные когерентные волны, накладываясь друг на друга, интерферируют между собой. Учитывая амплитуды и фазы вторичных волн, можно рассчитать амплитуду результирующей волны в любой точке пространства.

В качестве примера объяснения дифракции на основе принципа Гюйгенса – Френеля, рассмотрим преграду с узкой щелью, на которую падает плоская волна (рис. 3.11).

Рис. 3.11

В момент времени фронт волны находится в этой щели и его каждая точка является источником вторичных когерентных сферических волн, проходящих за время dt расстояние . Положение фронта волны в момент времени находится, как огибающая фронтов вторичных волн. Поскольку скорость волны в каждой точке волнового фронта перпендикулярна к нему, то имеются участки фронта волны, обеспечивающие проникновение света в область геометрической тени (см. рис. 3.11). Если размеры этих участков фронта волны соизмеримы с размерами щели, то дифракция света будет наблюдаться. Если же они существенно меньше размеров щели, то свет будет проходить через щель в соответствии с законами геометрической оптики, а явление дифракции будет не заметно [5].

3.3.1. Метод зон Френеля

Рассмотрим точечный источник света S, от которого в однородной среде распространяется сферическая волна, возбуждающая в точке P световое колебание (рис. 3.12).

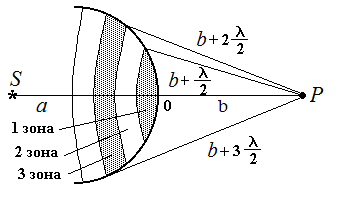
Рис. 3.12

Для нахождения амплитуды световой волны в точке P воспользуемся принципом Гюйгенса – Френеля. Пусть a = 0S – расстояние от точечного источника S света до волнового фронта, а b = 0P – расстояние от фронта волны до точки наблюдения P. Френель разбил волновой фронт на кольцевые зоны – зоны Френеля, построенные так, что расстояния от краев соседних зон до точки наблюдения P отличаются на ( – длина световой волны в той среде, в которой распространяется волна).

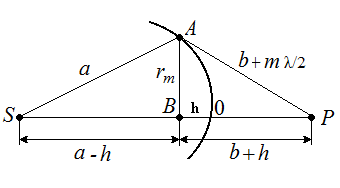
Рис. 3.13

Выражая радиус r_m произвольной зоны Френеля с номером m, с помощью теоремы Пифагора из SAB и ABP, и учитывая, что высота сферического сегмента h мала (см. рис. 3.13) получим:

. (3.18)

Если волна плоская (источник света удален на бесконечность: ), то радиус r_m зоны Френеля с номером m может быть выражен:

(3.19)

Расчеты показывают, что на полностью открытом волновом фронте укладывается огромное количество зон Френеля, причем площади всех зон примерно одинаковы. Однако, с увеличением номера зоны Френеля, уменьшается ее угловой размер (угол, под которым эта зона видна из точки наблюдения) и увеличивается расстояние от нее до точки наблюдения P. Все это приводит к тому, что с увеличением номера зоны амплитуда А_m колебания, возбуждаемого вторичной волной, приходящей от зоны Френеля с номером m, в точке P уменьшается. Таким образом, для амплитуд колебаний, возбуждаемых в точке P наблюдения зонами Френеля, справедливы неравенства

Кроме того амплитуда световой волны, приходящей в точку наблюдения от зоны с номером m может быть выражена в виде

.

Учтем, что согласно построению зон Френеля, волны, приходящие в точку наблюдения P от соседних зон, имеют оптическую разность хода (что соответствует разности фаз, равной π) и, в соответствии с условием интерференционного минимума, ослабляют друг друга. Поэтому амплитуду результирующей световой волны в точке P можно найти в виде:

, или

При полностью открытом волновом фронте , поэтому вклад зоны Френеля с номером N пренебрежимо мал по сравнению с вкладом от первой зоны Френеля ( ).

Таким образом, при полностью открытом волновом фронте, амплитуда световой волны в точке P равна половине амплитуды, создаваемой только лишь одной первой (центральной) зоной Френеля

. (3.20)

Если на пути световой волны поместить непрозрачный экран с отверстием, открывающим только одну первую зону Френеля, то амплитуда световых колебаний в точке P будет равна A₁, т.е. в два раза больше, а интенсивность света ( ) – в четыре раза больше, чем при отсутствии экрана.