13. Теpмодинамические хаpактеpистики химических пpоцессов. Теpмодинамический анализ.

Химическое превращение – качественный скачек, при котором исчезают одни вещества и образуются другие. При этом происходит перестройка электронных структур атомов и молекул, которая сопровождается выделением или поглощением теплоты, света, электричества (превращение химической энергии в другой вид энергии).

Реакции, протекающие с выделением энергии, чаще всего в виде тепла, называют экзотермическими, а реакции, при которых энергия поглощается – эндотермическими.

Энергетический эффект химического процесса возникает за счет изменения в системе внутренней энергии U или энтальпии H.

Внутренняя энергия – форма энергии, скрытая в веществах и освобождающаяся при химических процессах. Она складывается из энергии движения и взаимодействия молекул, энергии движения и взаимодействия ядер и электронов в атомах и молекулах, внутриядерной энергии.

Внутренняя энергия является функцией состояния вещества. Пусть в результате какого-либо процесса система переходит из состояния 1 (U₁) в состояние 2 (U₂), при этом из внешней среды поглощается теплота Q, и система совершает работу A против внешних сил:

U₂ = U₁ + Q – A или ΔU = Q – A (1)

Для химических реакций под работой против внешних сил в основном подразумевается работа против внешнего давления A = p(V₂ – V₁) = pΔV. Уравнение (1) выражает закон сохранения энергии, изменение внутренней энергии не зависит от способа проведения процесса, а определяется только начальным и конечным состояниями системы.

Если при реакции не происходит изменения объема ΔV = 0 (изохорный процесс), то A = 0; ΔU = Q. В случае изохорной химической реакции изменение внутренней энергии системы равно, но противоположно по знаку тепловому эффекту этой реакции.

В химии чаще всего имеют дело с изобарными процессами, то есть процессами, происходящими при постоянном давлении. Здесь удобно пользоваться величиной энтальпии H = U + pV.

A = pΔV → ΔH = ΔU + pΔV или ΔU = ΔH – pΔV

ΔU = Q – A Q – A = ΔH – pΔV → ΔH = Q_p

Итак, изменение энтальпии равно, но противоположно по знаку тепловому эффекту реакции, проведенной при постоянном давлении и постоянной температуре.

При экзотермических реакциях теплота выделяется, величины U и H уменьшаются, а ΔU и ΔH – отрицательны.

При эндотермических реакциях теплота поглощается, U и H увеличиваются, а ΔU и ΔH – положительны.

Для того, чтобы можно было сравнивать энергетические эффекты различных процессов, термохимические расчеты обычно относят к 1 молю вещества и стандартным условиям: Р = 1 атм (101325 Па) и Т = 25^oС (298,15 К).

Термодинамический анализ химико-технологических процессов

Позволяет сделать вывод о направлении протекания процесса (вправо или влево), предварительно выбрать условия проведения процесса, определить равновесный состав продуктов реакции, а также рассчитать тепловые эффекты.

Величины, характеризующие состояние термодинамических систем, называются термодинамическими параметрами. К ним относятся: температура, давление, удельный объем, плотность, удельная внутренняя энергия и др.

Термодинамические параметры делятся на экстенсивные и интенсивные. Параметры, которые пропорциональны массе системы, называются экстенсивными: это объем, внутренняя энергия, энтальпия, энтропия. Экстенсивные параметры обладают свойством аддитивности (их можно складывать).

Интенсивные параметры не зависят от массы термодинамической системы: это температура, давление, а также экстенсивные величины, отнесенные к единице массы или объема системы (удельная теплоемкость, плотность и др.).

Изменение интенсивных параметров с целью ускорения химико-технологических процессов называется интенсификцией.

14. Равновесие химических pеакций. Пpинцип Ле-Шателье. Константа равновесия на пpимеpе pеакции aA+bB=dD. Зависимость константы pавновесия от темпеpатуpы.

Химическим равновесием называется такое состояние обратимой химической реакции aA + bB = cC + dD, при котором с течением времени не происходит изменения концентраций реагирующих веществ в реакционной смеси. Состояние химического равновесия характеризуется константой химического равновесия:

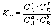, (1.1)

где C_i – концентрации компонентов в равновесной идеальной смеси.

Константа равновесия может быть выражена также через равновесные мольные доли X_i компонентов:

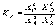. (1.2)

Для реакций, протекающих в газовой фазе, константу равновесия удобно выражать через равновесные парциальные давления P_i компонентов:

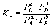. (1.3)

Для идеальных газов P_i = C_iRT и P_i = X_iP, где P – общее давление, поэтому K_P, K_C и K_X связаны следующим соотношением:

K_P = K_C (RT) ^c+d–a–b = K_XP ^c+d–a–b. (1.4)

Константа равновесия связана с 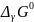 химической реакции:

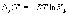 (1.5)

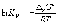 (1.6)

Изменение 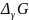  или 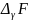  в химической реакции при заданных (не обязательно равновесных) парциальных давлениях P_i или концентрациях C_i компонентов можно рассчитать по уравнению изотермы химической реакции (изотермы Вант-Гоффа):

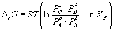. (1.7)

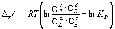. (1.8)

Согласно принципу Ле Шателье, если на систему, находящуюся в равновесии, оказать внешнее воздействие, то равновесие сместится так, чтобы уменьшить эффект внешнего воздействия. Так, повышение давления сдвигает равновесие в сторону уменьшения количества молекул газа. Добавление в равновесную смесь какого-либо компонента реакции сдвигает равновесие в сторону уменьшения количества этого компонента. Повышение (или понижение) температуры сдвигает равновесие в сторону реакции, протекающей с поглощением (выделением) теплоты.

Количественно зависимость константы равновесия от температуры описывается уравнением изобары химической реакции (изобары Вант-Гоффа)

 (1.9)

и изохоры химической реакции (изохоры Вант-Гоффа)

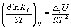. (1.10)

Интегрирование уравнения (1.9) в предположении, что 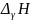  реакции не зависит от температуры (что справедливо в узких интервалах температур), дает:

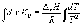 (1.11)

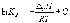 (1.12)

где C – константа интегрирования. Таким образом, зависимость ln K_P от 1/Т должна быть линейной, а наклон прямой равен – /R.

Интегрирование в пределах K₁, K₂, и T_1, T₂ дает:

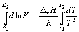 (1.13)

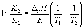 (1.14)

По этому уравнению, зная константы равновесия при двух разных температурах, можно рассчитать  реакции. Соответственно, зная  реакции и константу равновесия при одной температуре, можно рассчитать константу равновесия при другой температуре.