Определение 6. Множество из с называется областью, если открыто и связно.

Отметим, простой и понятный с виду факт, доказательство которого достаточно непросто.

Теорема 1 (Жордана). Любая жорданова кривая разбивает плоскость на две непересекающиеся области, общей границей которых она является. При этом одна из областей, называемая внутренностью , ограничена, а другая, называемая внешностью  и содержащая бесконечно удаленную точку, не ограничена .

Символ мы сейчас поясним. В комплексном анализе нет понятия, т.к. комплексные числа не сравнимы. Но пополнению комплексных чисел бесконечно удаленной точкой можно придать естественный геометрический вид.

Множество называют расширенной комплексной плоскостью. Для наглядного изображения расширенной комплексной плоскости проведем специальное геометрическое построение.

Введем в пространстве систему координаттак, чтобы плоскость С совпала с плоскостьюи чтобы осиисовпали с осямиикомплексной плоскостиz. Построим сферу S радиуса с центром в точке, которая касается комплексной плоскости в начале координат.

Рис.4

Точки удовлетворяет уравнению

Точку обозначим черезN и будем соединять ее с различными точками сферы прямолинейными лучами с началом вN и отмечать на каждом луче точку встречи его с плоскостью С. Тогда все точки сферы, за исключением точкиN, спроектируются на плоскость С. Этим установлено взаимно-однозначное соответствие между множествами С и. Если условимся, что, то получим взаимно одзначное соответствие между множествамииS. Это соответствие называется стереографической проекцией. Сферу S при этом называют сферой Римана.

Установим связь между координатами точке и. Координаты точкиудовлетворяют уравнению сферы, а условие, что точкиN,илежат на одной прямой, имеет вид

.

Следовательно,

Принимая во внимание уравнение сферы и последнее равенство, имеем

откуда

Теперь можно выразить переменные , лежащие на сфере, через соответствующие точки плоскости, черезx, y, z :

Получились «обратные» формулы, вместе с «прямыми» они называются основными формулами стереографической проекции.

Отметим два важных свойства стереографической проекции

Теорема 2. Стереографическая проекция обладает свойствами:

1. при стереографической проекции окружности всегда переходят в окружности ( при этом прямая на плоскости С считается окружностью бесконечного радиуса);

2. если две кривые на сфере S пересекаются в точке М, а касательные к этим кривым в точке М образуют угол , то и угол между касательными к стереографической проекции этих кривых в точке их пересечения также равен, т.е. величины углов при стереографической проекции сохраняются .

Для большей наглядности изложенного выше воспользуемся географической терминологией. Плоскость, проходящая через центр сферы параллельно плоскости , называетсяэкваториальной. Согласно принятой терминологии, точка лежит на параллели с широтой , если радиус-вектор с началом в центре сферыS образует угол  с экваториальной плоскостью, причем в верхней по отношению к этой плоскости части сферы  изменяется от 0 до , а в нижней части сферы – отдо 0. Точки сферы, имеющие одну и туже широту, образуют параллель данной широты. Долготой точки называют. Совокупность точек данной долготы образует полумеридиан этой долготы. Точка N называется северным полюсом, а начало координат 0 – южным полюсом.

Перейдем к рассмотрению примеров.

Пример 2.1. Найти на сфере Римана образы а) точки , б) области.

Решение. а) точка имеет координаты,. Тогда координаты точки образа на сфере Римана будут:

,,.

б) уравнение области на плоскостиxОy будет иметь вид:

Или раскрывая скобки и преобразовывая:

В силу основных формул стереографической проекции :

Т.к. знаменатель всегда положителен, для конечных точек плоскости, то

–уравнение в совокупности с уравнением сферы и будет уравнением участка сферы Римана, на который отображается данная область.

Пример 2.2. Выяснить геометрический смысл:

а) , б),.

Решение. а) данная область представляет собой все точки плоскости, за исключением круга с центром в точке (0, -2) и радиусом 3. (Рис.5).

Рис.5

б) область, изображенная на рис. 6.

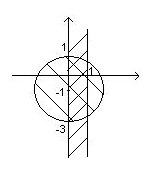
Рис.6

Пример 2.3. Какие кривые определяются следующими уравнениями (указать множество точек плоскости и порядок их похождения); представить кривые графически:

а);, б) построить кривую.

Решение . а). Представим число z в виде , где,.

Решаем систему:

Таким образом, кривая – это ветвь гиперболы, лежащая в области x>0, y>0. см Рис. 7.

Рис.7

При обход происходит в направлении 1, при– в направлении 2.

б) строим кривую .

Рис.8

3. Элементарные функции комплексного переменного

Определение 7. Говорят, что на множестве М из С задана функция f, если задан закон, по которому каждой точке z из М ставиться в соответствие комплексное число w ( конечное или бесконечное). Обозначается

или.

Хотя мы пишем – функция вроде бы зависит только от z , мы предполагаем, что она может зависеть и от . Этим и объясняется дальнейшее продолжение записи

,

т.е. задание комплекснозначной функции равносильно заданию двух вещественных функций. Функцию называют вещественной частью и – называют мнимой частью функции f.

Если еще , то, полагая, можно записать эту функцию в виде двух соотношений (полярное задание)

.

Т.к. аргумент не определен в точках , в этом случае нам нужно исключить его из рассмотрения. Последнее задание не пользуется такой популярностью, как задание функции с помощью двух вещественных функцийи.

Согласно определению 7 всякая функция однозначна (т.е. каждому z соответствует только одно w). Если мы будем рассматривать многозначные функции, то будем оговаривать это особо. Если функция преобразует различные точки в различные, то она называется взаимно однозначной или однолистной. Рассмотрим примеры некоторых элементарных функций.

w = z², z  C, однозначная функция, корректно определена, т.к введено произведение комплексных чисел.

, z  C, однозначная функция, определена на основании формулы Эйлера и вещественной функции .

z  C, однозначная функция, определяется опираясь на функцию .

z  C, однозначная функция определяется опираясь на функцию .

w = является многозначной функцией, определяется, как функция обратная .

w = ln z = ln r + i ,  = arg z  (-,], D = C\{0}, однозначная функция.

w = Arg z = arg z + 2k, (k-любой целое) многозначная функция.

w = Ln z = ln r + i  + 2ik,  = arg z  (-,], k-целое, D = C\0, многозначная функция, определяется как обратная функция к .

w = z^b = e^{b Ln z} может быть для некоторых b многозначной ( для натуральных b определение согласуется с операцией возведения в степень путём перемножения ).

Если функция f(z) однозначная, то можно обычным образом определить обратную функцию . Для этого обозначим черезD область определения функции f(z), а область ее значений через  . Обратная функция f ^-1 будет определена на  и каждому значению w из  будет сопоставлять все те значения z из D для которых f(z) = w. Обратная функция не обязана быть однозначной.

Если f и однозначные, то отображение z w = f(z) будет однолистным (отображение взаимно однозначное ).

Пример: функция w=z² отображает однолистно область D={|z|<1,0<arg z < } верхний полукруг на круг с разрезом по положительной вещественной оси.

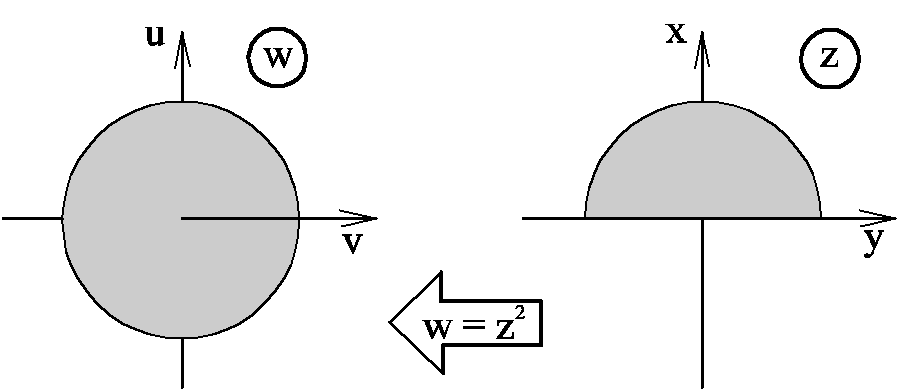
Рис.9

При исследовании многозначных функций выделяют однозначные ветви. Например, рассмотрим функцию , в качестве области определения D возьмём всю комплексную плоскость с вырезом по положительной части действительной оси, x[0,). В этой области рассмотрим функции (здесь главное значение аргумента комплексного числа считается выбираемым в диапазоне 0 arg z < 2). Эти функции представляют собой однозначные ветви исходной функции в области D. Первая отображает область D на верхнюю полуплоскость, вторая функция отображает область D на нижнюю полуплоскость. Однозначные ветви можно выделять по разному.

Можно определить элементарные функции используя их вещественные разложением в ряды Тейлора.

;

;

;

Пример 3.1. Представить в алгебраической форме .

Решение. Найдем модуль и аргумент числа стоящего под логарифмом

.

Пользуясь формулой главного значения логарифма

.

Пример 3.2. а) Найти образ линии Rez = 1 при отображении w = f(z) = Rez/z.

б) Найти образ полуполоса , , при отображении

Решение . а).– это все числа вида, где.

, . Данная кривая и будет являться образом линии. Это будет окружность с центром в точке (0.5, 0) радиуса 0.5.

Рис.9

б).

Рассмотрим, как отображаются линии, являющиеся границами заданной области.

1. отрезок у=0, 0<x< отображается в w=cos(x). Т.е. w=u, где u(-1, 1).

2. Луч x=0, -<y<0 отображается в w=cos(iy)=ch(y), т.е. w=u(1, ).

3. Луч x=, -<y<0 отображается в w=-cos(iy)=-ch(y), т.е. w=u(, 1).

Таким образом, граница данной фигуры переходит во все точки действительной оси u (в комплексной плоскости с координатами u, v) кроме точек –1 и 1. Значит, наша фигура отобразится в верхнюю или нижнюю полуплоскость комплексной плоскости w. Узнаем, в какую именно.

.

Рассмотрим, какие значения принимает . Т.к. 0<x<, то sin(x)>0. y<0, следовательно, sh(y)<0. Таким образом, >0. То есть данная фигура отображается на всю верхнюю полуплоскость комплексной плоскости w.