
Frisk_2
.pdf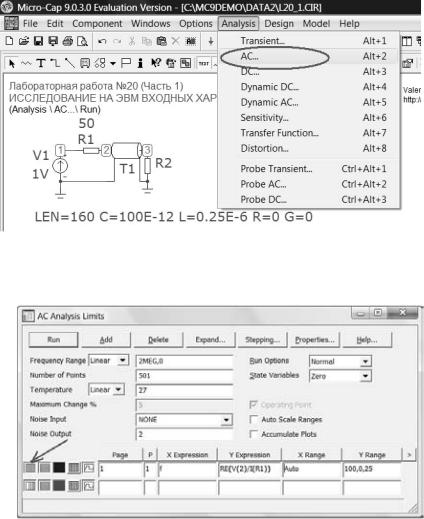
Рис. 19
На экране появится окно АС Analysis Limits, в котором задайте параметры так, как показано на рис. 20. Установите линейный масштаб по оси «X».
Рис. 20
Frequency Range «List», «2MEG,0» — диапазон частот (0 …2 МГц).
Number of Points «501» — число точек графика.
Page — номер страницы «1», на которой будет построен график.
P — номер окна «1», в котором будет построен график.
XExpression «f» — аргументы функции (текущая частота).
YExpression «Re(V(2)/I(R1))» — реальная часть входного сопротивления.
XRange «Auto» — интервал отображения аргумента по оси Х.
YRange «Auto» — интервал отображения функции по оси Y. Запустите построение, нажав кнопку Run.
На экране появиться график.
График с необходимыми построениями поместите в соответствующий раздел отчета, а данные
занесите в таблицу 1.
Сделайте вывод о форме полученной кривой.
100
4.3.2 Построение частотной зависимости входного сопротивления длинной линии для режима ХХ
Построим требуемую частотную зависимость
Im Z |
BX ( |
f |
|
= Im |
|
|
I1 |
|
, ( Im(V(2)/I(R1)) ). |
|
|
|
|
||||||||
|
|
) |
|
U |
|
|
||||
|
|
|
|
|
|
1 |
|
|
||
|
|
|
|
|
|
|
||||
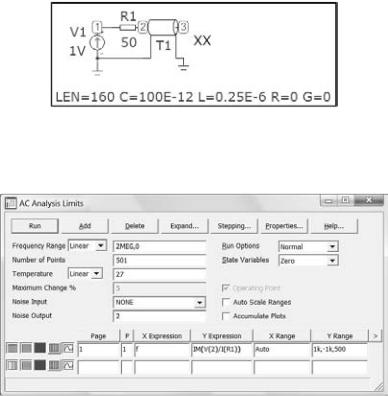
Вернитесь к исходной схеме (F3) и удалите (Delete) резистор сопротивления нагрузки R2 (рис. 21).
Рис. 21
Аналогично предыдущему пункты проведите частотный анализ (Analysis/AC…).
На экране появиться окно АС Analysis Limits, в котором задайте параметры так, как показано на рис. 22.
Рис. 22
Нажмите кнопку ОК.
На экране появится искомый график (рис. 23).
101
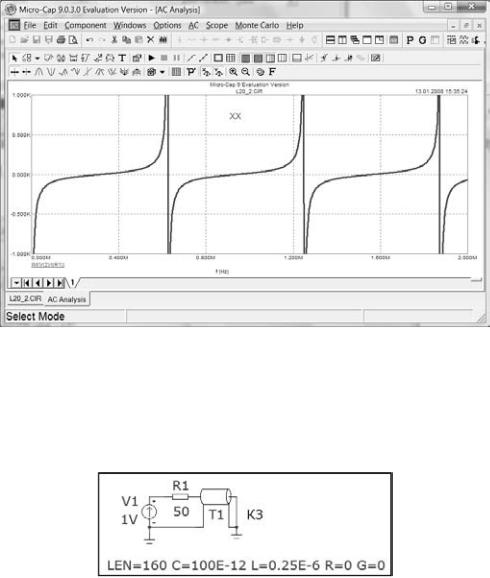
Рис. 23
Этот график с необходимыми построениями поместите в соответствующий раздел отчета, а данные занесите в таблицу 1.
Сделайте вывод о форме полученной кривой.
4.3.3 Построение частотной зависимости входного сопротивления длинной линии для режима КЗ
Вернитесь к исходной схеме (F3) и установите короткое замыкание на выходе линии (рис. 24).
Рис. 24
Аналогично предыдущему пункты проведите частотный анализ (Analysis/AC…).
Полученный график с необходимыми построениями поместите в соответствующий раздел отчета, а данные занесите в таблицу 1.
Сделайте вывод о форме полученной кривой.
В случае возникновения проблем загрузите с сайта поддержки учебного процесса
(http://frisk.newmail.ru/) для ознакомления файл L20_2.CIR (File\Open…).
5 Обработка результатов машинного эксперимента
Сравнить полученные графики и данные с графиками и данными, полученными в предварительном расчете. Сделать выводы по каждому машинному эксперименту.
102
6 Вопросы для самопроверки
1.Как рассчитывается входное сопротивление длинной линии с потерями и без потерь?
2.Получите формулы и качественно постройте зависимости входного сопротивления длинной линии от длинны линии при фиксированной частоте для различных режимов.
3.Как рассчитываются длины волны, излучаемая радиовещательной станцией и распространяемая в длинной линии?
4.Что называют реактивным шлейфом?
5.Что называется фазовой скоростью?
7 Содержание отчета
Отчет оформляется в формате MS Word. Шрифт Times New Roman 14, полуторный интервал. Для защиты лабораторной работы отчет должен содержать следующий материал: титульный
лист; цель работы; результаты машинного эксперимента; графики исследуемых зависимостей; выводы. К отчету должны быть приложены в напечатанном виде вопросы для самопроверки и ответы на них.
8Литература
1.Фриск В.В. Основы теории цепей. –М.: РадиоСофт, 2002. — 288 с.
2.Бакалов В.П., Дмитриков В.Ф., Крук Б.И. Основы теории цепей. –М.: Радио и связь, 2003. —
592 с.
3.Добротворский И.Н. Лабораторный практикум по основам теории цепей. –М.: Высшая школа, 1986. — 192 с.
4.Фуксо В. СВЧ цепи. Анализ и автоматизированное проектирование –М.: Радио и связь, 1990.
—288 с.
103
Лабораторная работа № 21
Исследование на ЭВМ ФНЧ Баттерворта
1 Цель работы
С помощью машинного эксперимента исследовать частотную характеристику фильтра нижних частот (ФНЧ). Получить практические навыки в синтезе фильтров Баттерворта.
2 Задание для самостоятельной подготовки
Изучить основные положения теории цепей о синтезе фильтров стр. 249–254 [1] и стр. 443–450 [2]. Выполнить предварительный расчет, письменно ответить на вопросы для самопроверки.
3 Предварительный расчёт
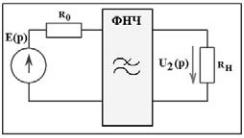
3.1 Синтезировать фильтр нижних частот (рис.1) с характеристикой Баттерворта, т.е. составить схему фильтра и определить величины её реактивных элементов по заданным численным значениям нагрузочных сопротивлений R0=RH=50 Ом и
f2=6 кГц — граничная частота ПП; f3=12 кГц — граничная частота ПЗ;
a=4 дБ — неравномерность ослабления в ПП; amin=15 дБ — минимальное ослабление в ПЗ.
Рис. 1
3.2 Рассчитать и построить кривую рабочего ослабления ap(f) при f [0; 2f3] кГц. На полученном графике обозначьте характерные точки частоты.
4 Порядок выполнения работы
Понятие о частотном фильтре
Электрическим частотным фильтром называется четырёхполюсник, рабочее ослабление которого в некоторой полосе частот (в полосе пропускания (ПП)) сравнительно невелико (0,1…3,0 дБ), а за пределами этой полосы частот (в полосе задержания (ПЗ)) имеет гораздо большую величину (10…60 дБ). Частотный диапазон между полосой пропускания и полосой задерживания называется переходной полосой (ПХ).
Граничную частоту между полосой пропускания и переходной полосой обозначают как f2. Граничную частоту между переходной полосой и полосой пропускания обозначают как f3 (рис. 2).
104
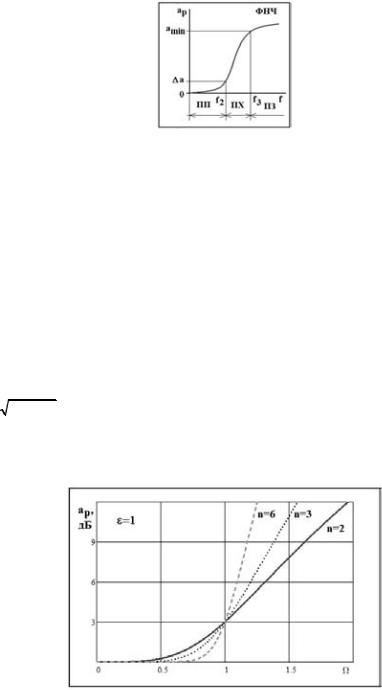
Рис. 2
f2, кГц — граничная частота ПП; f3, кГц — граничная частота ПЗ;
a, дБ — неравномерность ослабления в ПП;
amin, дБ — минимальное ослабление в ПЗ;
R0=RH, Ом — сопротивление генератора и нагрузки.
Фильтр с характеристикой Баттерворта
Рабочая передаточная функция ослабление фильтра имеет следующий вид
ap = 20 lg |
E |
|
2U2 |
||
|
|
|
R |
|
|
|
|
+10 lg |
H |
|
, дБ. |
|
R0 |
|||||
|
|
|
|
Рабочее ослабление фильтра Баттерворта выражается формулой ap = 10 lg (1+ ε2Ω2n ), дБ
где
ε = 100,1Δa −1 ;
ε — коэффициент неравномерности в ПП; Ω=f/f2 — нормированная частота;
n — порядок фильтра.
На рис. 3 показаны графики рабочего ослабления при ε=1 для различных n.
Рис. 3
Из этих графиков видно, что:
•при нулевой частоте рабочее ослабление ФНЧ Баттерворта равно нулю и по мере увеличения частоты монотонно возрастает;
105
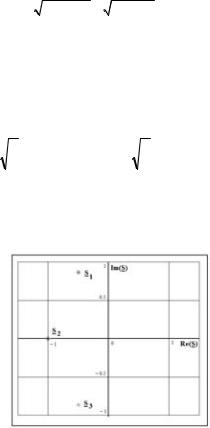
•на границе полосы пропускания (при Ω=1) рабочее ослабление фильтра равно 3 дБ независимо от величины порядка фильтра n;
•в полосе пропускания (Ω<1) увеличение порядка фильтра n, при фиксированной частоте, приводит к уменьшению рабочего ослабления;
•в полосе задерживания (Ω>1) увеличение порядка фильтра n, при фиксированной частоте, приводит к увеличению рабочего ослабления.
Пример синтеза ФНЧ Баттерворта
Пусть для синтеза заданы следующие исходные данные: f2=1 кГц — граничная частота ПП;
f3=1,5 кГц — граничная частота ПЗ;
a=3 дБ — неравномерность ослабления в ПП;
amin=10 дБ — минимальное ослабление в ПЗ; R0=RH=600 Ом — сопротивление генератора и нагрузки.
Расчеты будем проводить с точностью четыре знака после запятой.
1) |
Нормализуем f3 относительно f2 |
f3 |
|
1,5 |
|
|
ΩЗ = |
= |
=1,5; |
||
|
f2 |
1 |
|||
|
|
|
|
||
2) |
Находим коэффициент неравномерности ε |
|
|
|
|
ε = 100,1Δa −1 = 100,1 3 −1 = 0,9976 ; 3) Вычислим число реактивных элементов фильтра
A = |
100,1 amin −1 |
|
= |
100,110 −1 |
= 9,0428 , |
||||
ε2 |
|
0,99762 |
|
||||||
|
|
|
|
|
|
||||
N = |
|
lg ( A) |
= |
|
lg (9,428) |
= 2,7154 . |
|||
2 lg (Ω3 ) |
|
2 lg (1,5) |
|||||||
Округляем N до ближайшего целого большего числа n=3.
4) Находим полюсы передаточной функции. Для ФНЧ Баттерворта (n=3, k=1, 2, 3)
S k = n |
1 |
|
π |
2k +n −1 |
+ j n |
1 |
|
π |
2k +n −1 |
, |
||
ε |
cos |
2n |
|
ε |
sin |
2n |
|
|||||
|
|
|
|
|
|
|
|
|
||||
S1=–0,5004+j0,8667;
S2=–1,0008;
S3=–0,5004–j0,8667.
На рис. 4 показано расположение корней на комплексной плоскости.
Рис. 4
106
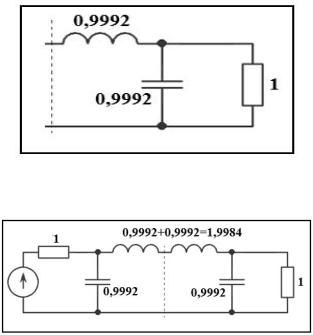
Заметим, что все корни лежат в левой полуплоскости. 5) Строим вспомогательные полиномы.
Так как n=3 — нечетное число, то составляем два вспомогательных полинома. Для первого выбираем корни с нечётными индексами
M(p)=(p–S1) (p–S3)=р2+1,0008р+1,0016.
Для второго выбираем корни с чётными индексами
N(P)=(p–S2)=р+1,0008.
6) Найдём коэффициент нормировки k и операторное входное сопротивление второй (правой) половины
фильтра |
|
|
N (0) |
|
|
|
|
|
|
|
|
|
k = |
= |
1,0008 |
= 0,9992 , |
|
||||
|
M ( p) |
M (0) |
|
1,0016 |
|
|||||
ZBX 2 ( p) = k |
= 0,9992 |
p2 +1,0008 p +1,0016 |
= |
0,9992 p2 + p +1,0008 . |
||||||
N ( p) |
|
|||||||||
|
|
|
|
|
p +1,0008 |
|
p +1,008 |
|||
По методике ускоренного синтеза [3], раскладываем входное сопротивление в цепную дробь (это можно сделать или в ручную или с помощью программы Сигма).
ZBX 2 ( p) = 0,9992s + |
1 |
|
, |
|
0,9992s +1 |
||||
|
|
|||
7) Из полученной цепной дроби выделяем нормированные элементы фильтра
LHOP=0,9992;
CHOP=0,9992;
RHOP=1;
R |
= |
1 |
= 1. |
|
|||
HOP0 |
|
RHOP |
|
|
|
||
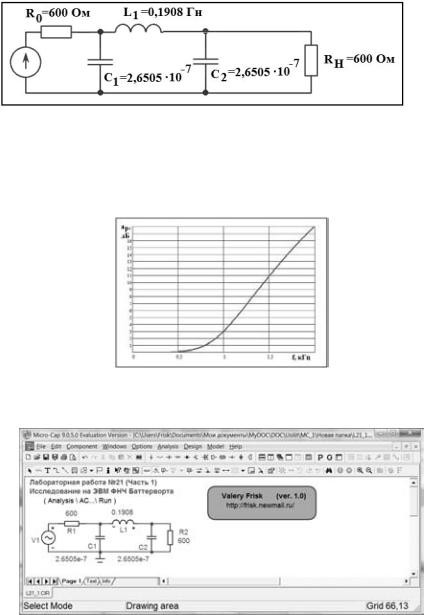
8) Этому разложению соответствует следующая схема правой половины фильтра (рис.5).
Рис. 5
9) Так как n=3 нечетное, то выбираем левую схему фильтра симметричную правой половине.
Рис. 6
10) Производим денормирование элементов и получаем окончательную схему фильтра (рис. 7).
107
|
|
|
|
|
|
R0 = RHOP0 RH = 1600 = 600 Ом, |
|
|
|||||||||
|
L1 = LHOP |
RH |
|
|
= 1,9984 |
600 |
|
= 0,1908 Гн, |
|
||||||||
|
2π f R |
|
2π 10001 |
|
|
||||||||||||
|
|
|
|
2 |
HOP |
|
|
|
|
|
|
|
|
||||
C |
= C |
|
= C |
|
|
RHOP |
|
= |
0,9992 |
|
1 |
|
|
= 2,6505 |
10−7 |
Ф. |
|
|
|
|
|
|
2π 1000 600 |
||||||||||||
1 |
|
2 |
|
HOP 2π f |
R |
|
|
|
|
|
|||||||
|
|
|
|
2 |
|
H |
|
|
|
|
|
|
|
|
|
||
Рис. 7
11) Строим график функции рабочего ослабления ФНЧ Баттерворта от частоты (рис. 8) по ниже приведённой формуле.
ap ( f ) = 10 |
|
2 |
|
f |
2n |
|
lg 1+ ε |
|
|
|
|
. |
|
|
f2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 8
Проверяем синтез с помощью программы Micro-Cap (рис. 9, 10 и 11).
Рис. 9
108
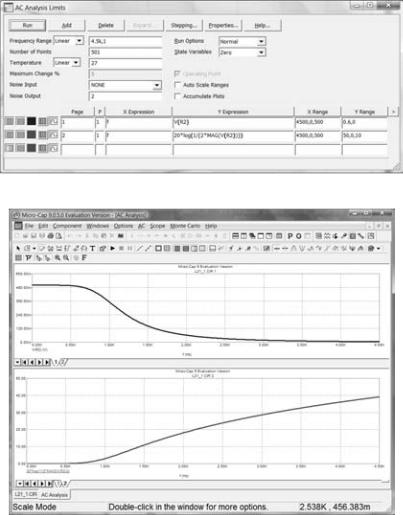
Рис. 10
Рис. 11
4.1 Проверить проведённый в предварительном расчёте синтез ФНЧ Баттерворта на ЭВМ. Для чего ввести синтезированную схему фильтра Баттерворта в программу схемотехнического проектирования Micro-Cap и построить с её помощью графики рабочего ослабления фильтра от частоты и АЧХ фильтра.
4.2 Запуск программы схемотехнического моделирования Micro–Cap
Включить ЭВМ и запустить программу Micro–Cap
C:\MC9DEMO\mc9demo.exe или
ПУСК\Все программы\Micro–Cap Evaluation 9\Micro–Cap Evaluation 9.
В появившемся окне Micro–Cap 9.0.3.0 Evaluation Version (рис. 12) собрать схему ФНЧ Баттер-
ворта.
109
