
Frisk_2
.pdf
На экране появится окно АС Analysis Limits, в котором задайте параметры так, как показано на рис. 31. Установите линейный масштаб по оси «X».
Рис. 31
Запустите построение, нажав кнопку Run. На экране появиться график.
График с отмеченными характерными точками поместите в соответствующий раздел отчета. Укажите ПП, ПХ и ПЗ. Сделайте вывод о форме полученной кривой.
5 Обработка результатов машинного эксперимента
Сравнить полученные графики с графиками, полученными в предварительном расчете. Сделать выводы по каждому машинному эксперименту.
6 Вопросы для самопроверки
1.Какой фильтр называется фильтром нижних частот?
2.Напишите формулу частотной зависимости рабочего затухания ФНЧ Баттерворта и перечислите основные свойства этой характеристики.
3.Что называют порядком фильтра Баттерворта, каким образом его рассчитывают?
4.Какая схема фильтра называется нормированной?
5.Каков алгоритм синтеза ФНЧ Баттерворта?
7 Содержание отчета
Отчет оформляется в формате MS Word. Шрифт Times New Roman 14, полуторный интервал. Для защиты лабораторной работы отчет должен содержать следующий материал: титульный
лист; цель работы; результаты машинного эксперимента; графики исследуемых зависимостей; выводы. К отчету должны быть приложены в напечатанном виде вопросы для самопроверки и ответы на них.
8Литература
1.Фриск В.В. Основы теории цепей. –М.: РадиоСофт, 2002. — 288 с.
2.Бакалов В.П., Дмитриков В.Ф., Крук Б.И. Основы теории цепей. –М.: Радио и связь, 2003. —
592 с.
3. Попов П.А. Применение частотных преобразований в теории цепей. –М.: Энергоатомиздат, 1986. -135 с.
120

Лабораторная работа № 22
Исследование на ЭВМ ФВЧ Чебышёва
1 Цель работы
С помощью машинного эксперимента исследовать частотную характеристику фильтра верхних частот (ФВЧ). Получить практические навыки в синтезе фильтров верхних частот Чебышёва.
2 Задание для самостоятельной подготовки
Изучить основные положения теории цепей о синтезе ФВЧ стр. 252–255 [1] и стр. 450–472 [2]. Выполнить предварительный расчет, письменно ответить на вопросы для самопроверки.
3 Предварительный расчёт
3.1 Синтезировать фильтр верхних частот (рис.1) с характеристикой Чебышёва, т.е. составить схему фильтра и определить величины её реактивных элементов по заданным численным значениям нагрузочных сопротивлений R0=RH=50 Ом и
F2=12 кГц — граничная частота ПП;
F3=6 кГц — граничная частота ПЗ;
a=3 дБ — неравномерность ослабления в ПП; amin=33 дБ — минимальное ослабление в ПЗ.
Рис. 1
3.2 Рассчитать и построить кривую рабочего ослабления ap(F) при F [0; 2F2] кГц. На полученном графике обозначьте характерные точки частоты.
4 Порядок выполнения работы
Преобразование схемы ФНЧ в схему ФВЧ
Возьмем схему ФНЧ с граничной частотой полосы пропускания равной 1 рад/с. Заменим в этой схеме все индуктивные элементы ёмкостными и все ёмкостные элементы индуктивными. Величины сопротивлений резисторов оставим неизменными. В результате таких замен получим схему фильтра верхних частот, у которого граничная частота полосы пропускания будет такой же, как и у схемы ФНЧ, 1 рад/с. Полоса пропускания ФВЧ будет при ω>1, а полоса задерживания ω<1.
ФНЧ, подвергаемый преобразованию в ФВЧ, называется ФНЧ-прототипом.
Граничную частоту между полосой пропускания и переходной полосой обозначают как F2. Граничную частоту между переходной полосой и полосой пропускания обозначают как F3 (рис. 2).
121
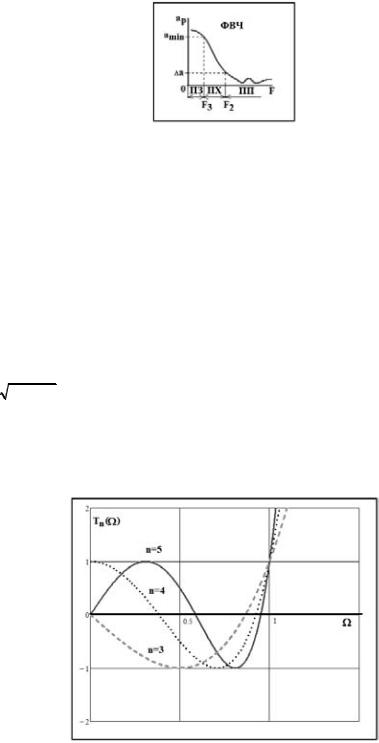
Рис. 2
F2, кГц — граничная частота ПП;
F3, кГц — граничная частота ПЗ;
a, дБ — неравномерность ослабления в ПП;
amin, дБ — минимальное ослабление в ПЗ;
R0=RH, Ом — сопротивление генератора и нагрузки.
Фильтр с характеристикой Чебышёва
Рабочая передаточная функция ослабление фильтра имеет следующий вид
|
E |
|
|
R |
|
|
|
ap = 20 lg |
|
|
+10 lg |
H |
|
, дБ. |
|
2U2 |
R0 |
||||||
|
|
|
|
|
Рабочее ослабление фильтра Чебышёва выражается формулой
|
p |
|
n ( |
Ω |
) |
a |
|
= 10 lg 1 |
+ ε2T 2 |
, дБ |
где
ε = 100,1Δa −1 ;
ε — коэффициент неравномерности в ПП;
Tn(Ω) — полином Чебышёва n-го порядка (T4(Ω)=8Ω4–8Ω2+1); Ω= F2/F — нормированная частота;
F — текущая частота; n — порядок фильтра.
На рис. 3 показаны графики полинома Чебышёва для различных n.
Рис. 3
122
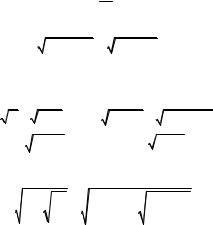
Из этих графиков видно, что:
•при 0<Ω<1 численное значение полинома Чебышёва изменяется по колебательному закону (осциллирует);
•при Ω>1 по мере увеличения частоты численные значения полинома Чебышёва
быстро возрастает.
Поскольку в формулу рабочего ослабления входит полином Чебышёва в квадрате, то в полосе пропускания и рабочее ослабление будет изменяться по колебательному закону (осциллировать).
Пример синтеза ФВЧ Чебышёва
Пусть для синтеза заданы следующие исходные данные: F2=2 кГц — граничная частота ПП;
F3=1 кГц — граничная частота ПЗ;
a=3 дБ — неравномерность ослабления в ПП;
amin=30 дБ — минимальное ослабление в ПЗ; R0=RH=600 Ом — сопротивление генератора и нагрузки.
Расчеты будем проводить с точностью четыре знака после запятой.
1)Перейдём к ФНЧ-прототипу
f2=F3=1 кГц, f3=F2=2 кГц.
2)Нормализуем f3 относительно f2
Ω3 = f3 = 2 = 2 ; f2 1
3) Находим коэффициент неравномерности ε
ε = 100,1Δa −1 = 100,1 3 −1 = 0,9976 ; 4) Вычислим число реактивных элементов фильтра прототипа
|
A = |
100,1 amin |
−1 |
= |
100,1 30 −1 |
=1003,8 , |
|
|||||
|
ε2 |
|
|
|
|
0,99762 |
|
|||||
|
ln( A + |
|
|
|
|
|
1003,8 −1) |
|
||||
N = |
A −1) |
|
ln( |
1003,8 + |
= 3,1502 . |
|||||||
|
|
= |
|
|
|
|
|
|
|
|||
ln(Ω3 + |
Ω32 −1) |
|
|
|
|
|
ln(2 + |
22 −1) |
||||
Округляем N до ближайшего целого большего числа n=4.
5) Находим полюсы передаточной функции. Для ФНЧ Чебышёва (n=4, k=1, 2, 3, 4)
|
x = n |
1 |
+ |
|
1 |
= |
4 |
|
1 |
|
+ |
|
|
1 |
|
|
=1,247 |
|
|
||||
|
ε |
|
ε2 |
|
|
|
0,99762 |
|
|
||||||||||||||
|
|
|
|
|
|
|
0,9976 |
|
|
|
|
|
|
||||||||||
S k = |
1 1 |
|
|
|
|
|
π |
2k −1 |
|
|
1 |
+ x |
|
|
|
π |
2k −1 |
|
, |
||||
2 |
|
− x |
sin |
|
2n |
|
+ j |
|
cos |
2n |
|
||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||||
S1=–0,0852+j0,9465;
S2=–0,2056+j0,392;
S3=–0,2056–j0,392;
S4=–0,0852–j0,9465.
На рис. 4 показано расположение корней на комплексной плоскости.
123
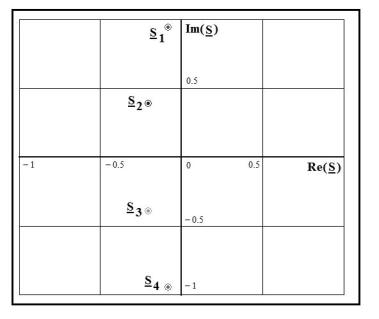
Рис. 4
Заметим, что все корни лежат в левой полуплоскости. 6) Строим вспомогательные полиномы.
Так как n=4 — чётное число, то составляем вспомогательный полином F(p). Для него выбираем корни с нечётными индексами
F(p)=M(p)–jN(p)=(p–S1) (p–S3)=р2+0,2908р+0,3886–j(0,5544р+0,1612),
Следовательно М(р)=р2+0,2908р+0,3886; N(p)=0,5544р+0,1612.
7) Найдём операторное входное сопротивление второй (правой) половины фильтра (в нашем случае k=1) |
||||
ZBX 2 ( p) = k |
M ( p) |
= |
p2 + 0,2908 p + 0,3886 |
. |
N ( p) |
|
|||
|
|
0,5544 p + 0,1612 |
||
По методике ускоренного синтеза [3], раскладываем входное сопротивление в цепную дробь (это можно сделать или в ручную или с помощью программы Сигма).
ZBX 2 ( p) = 1,8038 p + |
1 |
, |
|
1,4267 p + 2,4107 |
|||
|
|
8) Из полученной цепной дроби выделяем нормированные элементы фильтра
LHOP=1,8038;
CHOP=1,4267;
RHOP=2,4107.
Мы получили, что RНОР≠1, поэтому после синтеза R0≠RH.
9) Этому разложению соответствует следующая схема правой половины фильтра (рис.5).
124
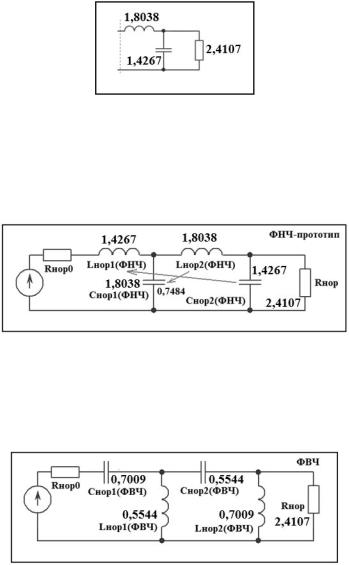
Рис. 5
10) Так как n=4 чётное, то выбираем левую схему фильтра-прототипа дуальную правой половине (рис. 6).
LHOP1(ФНЧ)=1,4267;
LHOP2(ФНЧ)=1,8038;
CHOP1(ФНЧ)=1,8038;
CHOP2(ФНЧ)=1,4267.
Рис. 6
11) Переходим от схемы ФНЧ-прототипа к схеме ФВЧ (рис. 7), делая следующие замены.
CHOP1(ФВЧ)=1/LHOP1(ФНЧ)=1/1,4267=0,7009;
CHOP2(ФВЧ)=1/LHOP2(ФНЧ)=1/1,8038=0,5544;
LHOP1(ФВЧ)=1/CHOP1(ФНЧ)=1/1,8038=0,5544; HOP2(ФНЧ)=1/1,4267=0,7009.
Рис. 7
12) Производим денормирование элементов и получаем окончательную схему фильтра (рис. 8).
|
|
|
|
|
|
|
|
|
|
|
RH = 600 Ом, |
|
|
|
|||||
|
R0 |
= |
|
|
|
1 |
|
RH |
= |
1 |
|
|
600 |
= 103,244 Ом, |
|||||
|
|
R |
2 |
|
2,41072 |
||||||||||||||
|
|
|
|
|
|
HOP |
|
|
|
|
|
|
|
|
|
|
|||
L1 |
= LHOP1 ФВЧ |
|
|
|
|
RH |
= |
0,5544 |
|
|
600 |
|
= 0,011 Гн, |
||||||
) 2πF R |
2π 2000 2,4107 |
||||||||||||||||||
|
( |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
2 |
|
HOP |
|
|
|
|
|
|
|
|
||
L2 = LHOP2(ФВЧ ) |
|
|
|
RH |
|
|
= 0,7009 |
|
|
|
600 |
|
= 0,0139 Гн, |
||||||
|
2πF R |
|
2π 2000 2,4107 |
|
|||||||||||||||
|
|
|
|
|
|
|
2 |
|
HOP |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
125 |
|
|
|
|
|
|
|
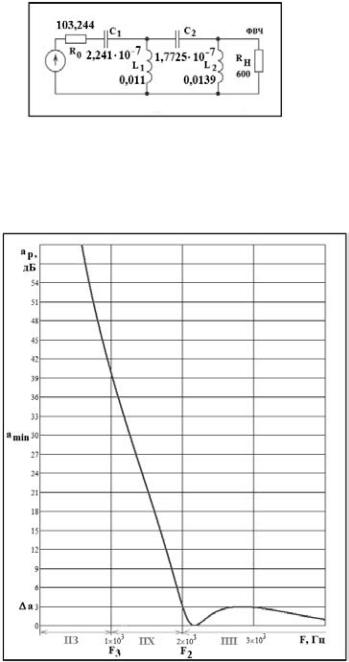
C |
= C |
|
|
|
RHOP |
|
|
= 0,7009 |
2,4107 |
|
= 2,241 10−7 |
Ф, |
|
( |
|
) 2πF R |
2π 2000 600 |
||||||||||
1 |
|
ФВЧ |
|
|
|
|
|||||||
|
HOP1 |
2 |
H |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
C2 |
= CHOP2(ФВЧ ) |
RHOP |
|
|
= 0,5544 |
2,4107 |
|
= 1,772510 |
−7 |
Ф. |
|||
2πF R |
|
2π 2000 600 |
|
|
|||||||||
|
|
|
|
2 |
H |
|
|
|
|
|
|
||
Рис. 8
13) Строим график функции рабочего ослабления ФНЧ Чебышёва от частоты (рис. 9) по ниже приведённой формуле.
|
|
(F ) = 10 lg |
|
+ ε |
2 2 |
F2 |
|
|
|
a |
p |
1 |
T |
|
|
|
. |
||
|
|||||||||
|
|
|
|
4 |
F |
|
|||
|
|
|
|
|
|
|
|
|
|
Рис. 9
126
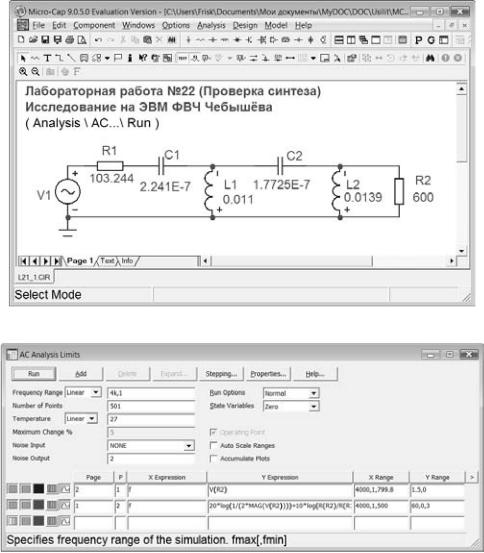
Проверяем синтез с помощью программы Micro-Cap (рис. 10, 11 и 12).
Рис. 10
Рис. 11
127
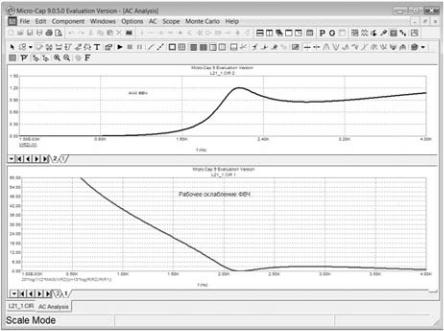
Рис. 12
4.1 Проверить проведённый в предварительном расчёте синтез ФBЧ Чебышёва на ЭВМ. Для чего ввести синтезированную схему фильтра Чебышёва в программу схемотехнического проектирования Mi- cro-Cap и построить с её помощью графики АЧХ фильтра и рабочего ослабления ФВЧ от частоты.
4.2 Запуск программы схемотехнического моделирования Micro–Cap
Включить ЭВМ и запустить программу Micro–Cap
C:\MC9DEMO\mc9demo.exe или
ПУСК\Все программы\Micro–Cap Evaluation 9\Micro–Cap Evaluation 9.
В появившемся окне Micro–Cap 9.0.5.0 Evaluation Version (рис. 13) собрать схему ФВЧ Чебышёва синтезированную в предварительном расчёте.
128
Рис. 13
4.2 Сборка схемы
Соберем схему содержащую источник синусоидального напряжения, два резистора, необходимое количество реактивных элементов полученных в предварительном расчете и земли.
4.2.1 Ввод источника синусоидального напряжения
Ввести источник синусоидального напряжения V1.
Откройте меню Component\Analog Primitives\Waveform Sources и выберите синусоидальный источник Sine Source (рис. 14).
129
