
Frisk_2
.pdf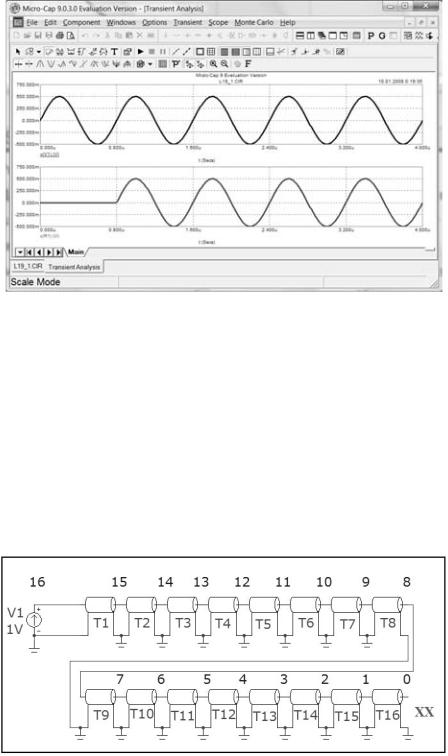
Рис. 21
Данные графики занесите в соответствующий раздел отчета. Отметьте на графике время запаздывания и занесите её величину в таблицу 1.
Замечание. Если кривые не появились, то на клавиатуре нажмите клавишу F9 и убедитесь, что все величины для построения графика введены правильно. Нажмите вновь кнопку Run.
Повторите этот эксперимент c другой длинной линии l=400 м. Вернитесь к исходной схеме, нажав на клавиатуре клавишу F3. Измените длину линии LEN=400. Для этого щелкните два раза на цифре 160 и введите 400. Повторите анализ.
Сделайте вывод о влиянии длины линии на величину времени запаздывания.
4.3.2 Исследование распределения напряжений вдоль линии для режима холостого хода
Вернитесь к исходной схеме (F3) и установите длину линии T1 10 м (LEN=10). Удалите R1. Путём копирования длинной линии T1 установите их ещё 15 штук. Общая длина линии составит 16х10=160 м. Добавьте необходимое количество элементов Земля (рис. 22).
80
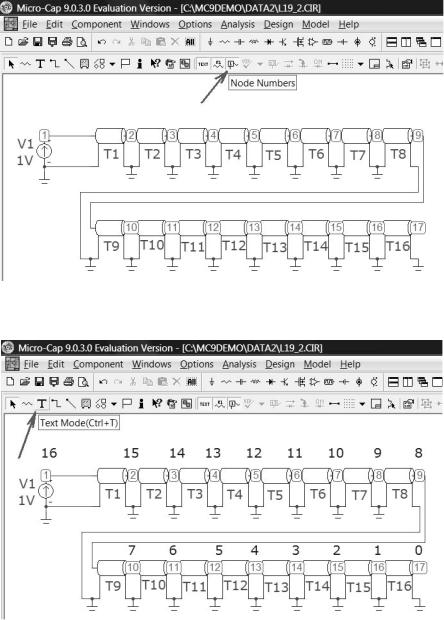
Рис. 22
Нажмите кнопку Нумерация узлов (Node Numbers) и убедитесь, что нумерация узлов такая, как показано на рис. 23.
Рис. 23
Используя кнопку Text Mode, подпишите узлы 17-0, …, 1-16 (рис. 24).
Рис. 24
Найдем значения действующих напряжений на каждом узле линии при фиксированной частоте f=1,25 МГц в табличном виде. Для этого в меню Analysis выберите команду запуска частотного анализа
AC… (рис. 25).
81
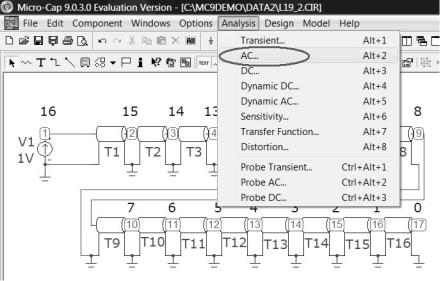
Рис. 25
На экране появиться окно АС Analysis Limits, в котором задайте параметры так, как показано на рис. 26. Установите линейный масштаб по оси «X».
82
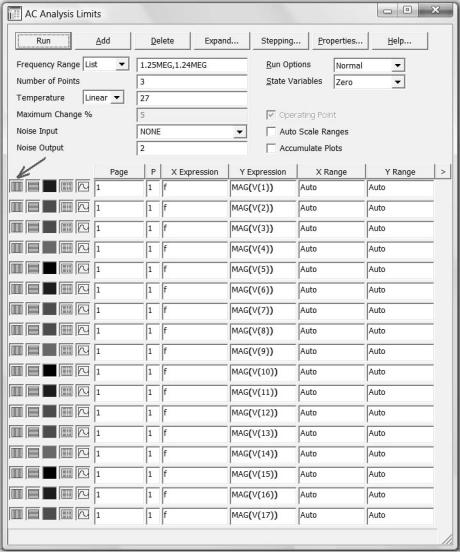
Рис. 26
Frequency Range «List», «1.25MEG,1.24MEG» — две частоты (1,24 и 1,25 МГц).
Number of Points «3» — число точек графика.
Page — номер страницы «1», на которой будет построен график. P — номер окна «1», в котором будет построен график.
XExpression «f» — аргументы функции (текущая частота).
YExpression «MAG(V(1))» — модуль действующего напряжения в узле 1.
XRange «Auto» — интервал отображения аргумента по оси Х.
YRange «Auto» — интервал отображения функции по оси Y. Запустите построение, нажав кнопку Run.
На экране появиться графики. Два раза щёлкните на поле графиков левой кнопкой мыши.
В появившемся окне Properties for AC Analysis выберите закладку Numeric Output.
В окне Curves установите галочки против всех функций и для каждой в окне Alias задайте новоё имя (MAG(V(1)) — V16, …, MAG(V(17)) — V0) и нажмите кнопку ОК (рис. 27).
83
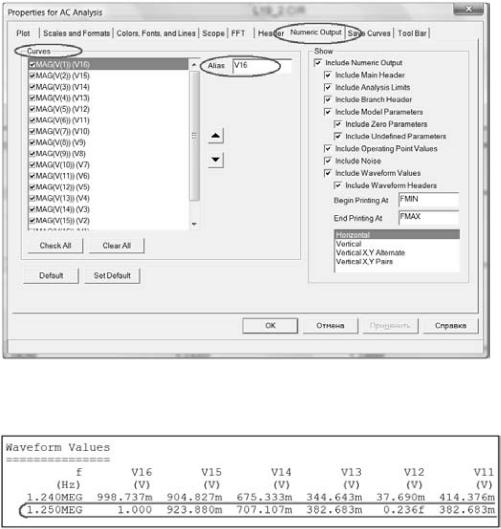
Рис. 27
Нажмите кнопку Run. Нажмите кнопку числового вывода F5. Найдите строчку Waveform Value (рис. 28).
Рис. 28
Выделите всю строчку с частотой 1,25 МГц (1.250MEG).
С помощью программы, например Microsoft Excel, постройте график распределения действующего значения напряжения вдоль линии в режиме холостого хода (рис. 29).
84
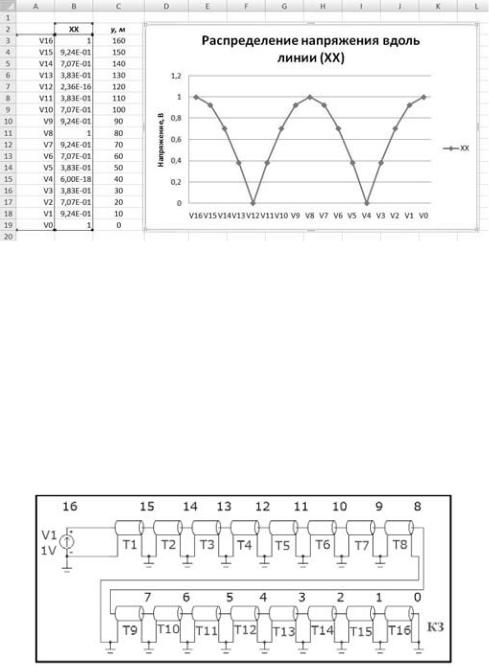
Рис. 29
Замечание. При переносе данных в Microsoft Excel следует десятичную точку заменить на запя-
тую, m на E-3, f на E-15.
На полученном графике обозначьте характерные точки (0, λ/4, λ/2, 3λ/4 и λ).
Определите по графику коэффициент бегущей волны (КБВ) и рассчитайте коэффициент отраже-
ния ρ.
График с необходимыми построениями поместите в раздел отчета, а данные занесите в соответствующие таблицы.
Сделайте вывод о форме полученной кривой.
4.3.3 Исследование распределения напряжений вдоль линии для режима короткого замыкания
Вернитесь к исходной схеме (F9, Ran, F3) и установите короткое замыкание на выходе линии
(рис. 30)
Рис. 30
Аналогично предыдущему пункты исследуйте распределение напряжения вдоль линии в режиме короткого замыкания (Analysis, AC…, удалите последнюю строчку т.к. V(17)=0, Run и так далее).
График (Microsoft Excel) с необходимыми построениями поместите в раздел отчета, а данные занесите в соответствующие таблицы.
Сделайте вывод о форме полученной кривой.
85
4.3.4 Исследование распределения напряжений вдоль линии для режима согласованной нагрузки
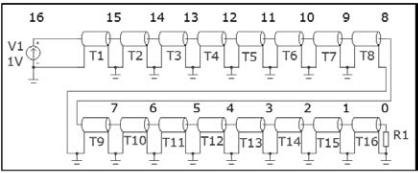
Вернитесь к исходной схеме (F9, Run, F3) и установите сопротивление нагрузки R1=ZB рассчитанное в #3.1 предварительного расчёта для линии длиной 160 м (рис. 31).
Рис. 31
Установите внутреннее сопротивление источника V1 RS=0 Ом.
Аналогично предыдущему пункты исследуйте распределение напряжения вдоль линии в режиме согласованной нагрузки (Analysis, AC…, восстановите последнюю строчку с V(17), Run и так далее).
График (Microsoft Excel) с необходимыми построениями поместите в раздел отчета, а данные занесите в соответствующие таблицы.
Сделайте вывод о форме полученной кривой.
4.3.5 Исследование распределения напряжений вдоль линии для режима несогласованной нагрузки
Вернитесь к исходной схеме (F9, Run, F3) и установите сопротивление нагрузки R1=2ZB для линии длиной 160 м.
Аналогично предыдущему пункты исследуйте распределение напряжения вдоль линии в режиме несогласованной нагрузки (Analysis, AC…, Run и так далее).
График (Microsoft Excel) с необходимыми построениями поместите в раздел отчета, а данные занесите в соответствующие таблицы.
Сделайте вывод о форме полученной кривой.
В случае возникновения проблем загрузите с сайта поддержки учебного процесса
(http://frisk.newmail.ru/) для ознакомления файл L19_2.CIR (File\Open…).
5 Обработка результатов машинного эксперимента
Сравнить полученные графики и данные с графиками и данными, полученными в предварительном расчете. Сделать выводы по каждому машинному эксперименту.
6 Вопросы для самопроверки
1. В каких случаях электрические цепи рассматривают как цепи с распределенными параметра-
ми?
2.Запишите уравнения передачи длинной линии с потерями и без потерь.
3.Что такое волновое сопротивление линии?
4.Что называют коэффициентом отражения от нагрузки?
5.Какие режимы работы в линии вы знаете? Приведите примеры.
86
7 Содержание отчета
Отчет оформляется в формате MS Word. Шрифт Times New Roman 14, полуторный интервал. Для защиты лабораторной работы отчет должен содержать следующий материал: титульный
лист; цель работы; результаты машинного эксперимента; графики исследуемых зависимостей; выводы. К отчету должны быть приложены в напечатанном виде вопросы для самопроверки и ответы на них.
8Литература
1.Фриск В.В. Основы теории цепей. –М.: РадиоСофт, 2002. — 288 с.
2.Бакалов В.П., Дмитриков В.Ф., Крук Б.И. Основы теории цепей. –М.: Радио и связь, 2003. —
592 с.
3. Добротворский И.Н. Лабораторный практикум по основам теории цепей. –М.: Высшая школа, 1986. — 192 с.
87
Лабораторная работа № 20
Исследование на ЭВМ входных характеристик длинной линии
1 Цель работы
С помощью машинного эксперимента проанализировать зависимость входного сопротивления длинной линии от частоты при различных сопротивлениях нагрузки. Получить практические навыки в проведении машинных экспериментов и обработки их результатов.
2 Задание для самостоятельной подготовки
Изучить основные положения теории цепей о резонансе напряжений стр. 238–239 [1], стр. 343– 352 [2], стр. 184–190 [3]. и стр. 174–175 [4]. Выполнить предварительный расчет, письменно ответить на вопросы для самопроверки.
3 Предварительный расчет
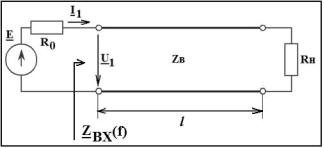
3.1 Длина линии без потерь равна l=160 м, погонная емкость C0=100 пФ/м, погонная индуктивность L0=0,25 мкГн (рис. 1) рассчитать:
•волновое сопротивление ZB;
•фазовую скорость VФ;
Рис. 1
Полученные данные записать в таблицу 1. ZB= Ом, VФ, = м/с
По предварительному расчету l=160 м, L0=0,25 мкГн, C0=100 пФ/м,
88

|
|
|
|
|
|
|
|
Таблица 1 |
|
|
|
|
|
|
|
Получено экспериментально |
|
||
|
По предварительному расчету |
|
|
||||||
|
l=160 м, L0=0,25 мкГн, C0=100 пФ/м, |
|
|
|
|
|
|||
|
|
ZB= Ом, VФ, = м/с |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
n |
f=n*[VФ/(4*l)], |
Re[ZBX(f)], |
Im[ZBX(f)], |
|
Im[ZBX(f)], |
Re[ZBX(f)], |
Im[ZBX(f)], |
Im[ZBX(f)], |
|
Гц |
Ом |
Ом |
|
Ом |
Ом |
Ом |
Ом |
|
|
|
|
(СН) |
(ХХ) |
|
(КЗ) |
(СН) |
(ХХ) |
(КЗ) |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.2 Рассчитать и построить кривую реальной части входного сопротивления Re[ZBX(f)] длинной линии без потерь от частоты f [0; 2] МГц для режима согласованной нагрузки (СН) RH=ZB.
На полученном графике обозначьте характерные точки частоты f:
VФ |
|
|
VФ |
|
|
VФ |
|
|
VФ |
|
|
VФ |
|
|
VФ |
||||||||||||
0, 1 |
|
|
, |
2 |
|
|
|
, |
3 |
|
|
|
, |
4 |
|
|
|
, |
5 |
|
|
|
, |
6 |
|
|
. |
|
|
|
|
|
|
||||||||||||||||||||||
|
4l |
|
|
|
4l |
|
|
|
4l |
|
|
|
4l |
|
|
|
4l |
|
|
|
4l |
||||||
Полученные данные записать в таблицу 1.
3.3 Рассчитать и построить кривую мнимой части входного сопротивления Im[ZBX(f)] длинной линии без потерь от частоты f [0; 2] МГц для режима холостого хода (ХХ) RH=∞.
На полученном графике обозначьте характерные точки частоты f:
VФ |
|
VФ |
|
VФ |
|
VФ |
|
VФ |
|
VФ |
||||||||||||
0, 1 |
|
|
, |
2 |
|
|
, |
3 |
|
|
, |
4 |
|
|
, |
5 |
|
|
, |
6 |
|
. |
|
|
|
|
|
|
|||||||||||||||||
|
4l |
|
|
4l |
|
|
4l |
|
|
4l |
|
|
4l |
|
|
4l |
||||||
Полученные данные записать в таблицу 1.
3.4 Рассчитать и построить кривую мнимой части входного сопротивления Im[ZBX(f)] длинной линии без потерь от частоты f [0; 2] МГц для режима короткого замыкания (КЗ) RH=0.
На полученном графике обозначьте характерные точки частоты f:
VФ |
|
|
VФ |
|
|
VФ |
|
|
VФ |
|
|
VФ |
|
|
VФ |
||||||||||||
0, 1 |
|
|
, |
2 |
|
|
|
, |
3 |
|
|
|
, |
4 |
|
|
|
, |
5 |
|
|
|
, |
6 |
|
|
. |
|
|
|
|
|
|
||||||||||||||||||||||
|
4l |
|
|
|
4l |
|
|
|
4l |
|
|
|
4l |
|
|
|
4l |
|
|
|
4l |
||||||
Полученные данные записать в таблицу 1.
4 Порядок выполнения работы
Однородная длинная линия, у которой погонное сопротивление R0 и погонная проводимость G0 равны нулю, называются линией без потерь. В такой линии элементарный отрезок длинной dx содержит только погонную индуктивность L0 и погонную емкость C0 (рис. 2).
89
