
Frisk_2_16_17_23
.pdf
Глава первая
ОПИСАНИЕ ЛАБОРАТОРНЫХ РАБОТ ПО ТЭЦ
Лабораторная работа № 16
Исследование на ЭВМ резонансных явлений в пассивном и активном последовательном колебательном контуре
1 Цель работы
С помощью программы Micro-Cap исследовать характеристики одиночного последовательного пассивного и активного колебательного контура при различных добротностях.
2 Задание для самостоятельной подготовки
Изучить основные положения теории цепей о резонансе напряжений стр. 84-97 [1], стр. 113-121 [2], стр. 4-18 [3], стр. 49-63 [4] и стр. 162-163, 168-170 [5]. Выполнить предварительный расчет, письменно ответить на вопросы для самопроверки.
3 Предварительный расчет
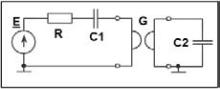
3.1 Рассчитать величину индуктивности L выбрав из заданного интервала величину ёмкости C [10; 40] нФ так, чтобы резонансная частота пассивного последовательного колебательного контура (рис. 1) f0=4,8 кГц.
Рис. 1
3.2 Рассчитать следующие параметры последовательного контура (U1=1 В): ρ — характеристическое сопротивление;
Q — добротность;
f1 — нижнюю граничную частоту; f2 — верхнюю граничную частоту;
П — абсолютную полосу пропускания; I0 — модуль входного тока при резонансе.
Расчеты провести для двух значений сопротивления R=160 и 640 Ом.
4
Полученные данные записать в таблицу 1.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По предварительному расчету |
|
|
Получено экспериментально |
|
|
|||||||||||
U1=1 В, f0=4,8 кГц, С=_____ Ф, L=_____ Гн. |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R, |
|
ρ, |
Q |
f1, |
f2, |
П, |
I0, |
|
f0, |
f0, |
|
I0, |
f1, |
f2, |
П, |
|
Q |
|
Ом |
|
Ом |
|
кГц |
кГц |
кГц |
А |
|
кГц |
Гц |
|
А |
кГц |
кГц |
кГц |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
160 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
640 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Гиратор |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
По предварительному расчету |
|
|
Получено экспериментально |
|
|
|||||||||||
U1=1 В, f0=5 кГц, С2=1 мкФ, G=0,1 См. |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
R, Ом |
|
|
|
С2, мкФ |
|
|
|
|
|
|
f0, кГц |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.3 На одном графике построить три зависимости входного сопротивления от частоты f [2; 8] кГц, R=160 Ом:
•модуля входного сопротивления |ZBX(f)|;
•действительной части входного сопротивления Re[ZBX(f)];
•мнимой части входного сопротивления Im[ZBX(f)].
На другом графике повторить эти построения для R=640 Ом.
3.4 Построить график зависимости фазы входного сопротивления ϕZвх(f)=arg[ZBX(f)] от частоты f [2; 8] кГц.
Построения провести на одном графике для двух значений сопротивления R=160 и
640Ом.
3.5Построить график резонансной кривой, т.е. зависимость модуля входного тока |I(f)|
последовательного контура от частоты f [2; 8] кГц.
Построения провести на одном графике для двух значений сопротивления R=160 и
640Ом.
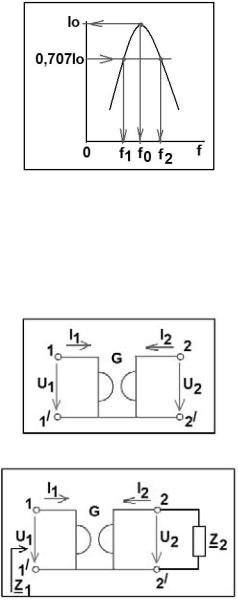
3.6Рассчитать значение ёмкости C1 так, чтобы резонансная частота активного последовательного колебательного контура с гиратором в качестве индуктивности (рис. 2) равнялась
f0=5 кГц. Принять R=0,1 Ом, C2=1 мкФ и G=0,1 См.
Полученные данные записать в таблицу 1.
Рис. 2
5

4 Порядок выполнения работы
Пассивный последовательный колебательный контур состоит из конденсатора, катушки индуктивности и резистора (рис. 1).
Из условия резонанса напряжений в последовательном пассивном колебательном контуре, записываемого в виде
Im(Z BX ) ,
где комплексное входное сопротивление контура
|
|
U |
1 |
|
|
1 |
|
|
Z BX = |
|
I |
|
= R + j |
ωL − |
|
|
, |
|
|
|
|
|
ωC |
|
||
можно найти резонансную частоту контура
ω |
L − |
1 |
= 0 , |
||
ω0C |
|||||
0 |
|
|
|
||
ω0 |
= |
|
1 |
= 0 , |
|
|
LC |
||||
|
|
|
|
||
итак как
ω0 = 2π f0 ,
окончательно получим f0 = 2π 1LC .
Остальные параметры последовательного контура вычисляются по следующим форму-
лам.
Характеристическое сопротивление
ρ = CL .
Добротность
Q = Rρ .
Нижняя граничная частота f1 = 2fQ0 ( 1+ 4Q2 −1).
Верхняя граничная частота f2 = 2fQ0 ( 1+ 4Q2 +1).
Абсолютная полоса пропускания
П=f2-f1.
Модуль входного тока при резонансе
I0 = UR1 .
Резонансная кривая тока при условии, что меняется только частота источника напряже-
ния
I (ω) = |
|
|
|
U1 |
|
|
. |
|
|
|
|
|
|||
|
R |
2 |
ωL − |
1 |
|||
|
|
+ |
|
|
|||
|
|
||||||
|
|
|
|
|
ωC |
||
6
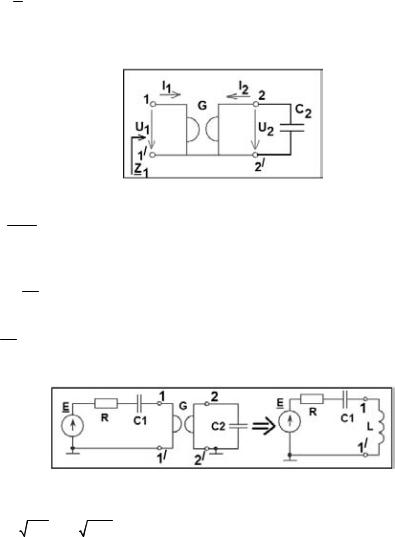
Определение добротности по резонансной кривой
Добротность Q последовательного контура можно определить при помощи резонансной кривой по формуле
Q = |
|
|
f0 |
|
|
|
|
. |
|
f |
2 |
− f |
||
|
|
1 |
|
|
Необходимые для этого построения показаны на рис. 3.
Рис. 3
Гиратор
Гиратором называется четырехполюсник (рис. 4), описываемый системой уравнений
I1 = −GU 2 ,
I 2 = −GU1
где G — проводимость гиратора (коэффициент гирации).
Рис. 4
Подключим к выходу гиратора комплексное сопротивление нагрузки Z2 (рис 5).
Рис. 5 Входное сопротивление нагруженного гиратора в этом случаи будет равно
Z |
1 |
= |
U |
1 = |
−I 2 |
|
= |
1 |
, |
|
|
||||||||||
|
|
|
|
|||||||
|
|
I1 |
G2 |
U |
2 |
|
G2 Z 2 |
|||
|
|
|
|
|||||||
7
т.к.
I 2 = −U 2 . Z1
Полученное выражение показывает, что с помощью гиратора нагруженного на конденсатор можно имитировать индуктивность. Действительно, подключим к гиратору конденсатор С2
(рис. 6).
Рис. 6 В этом случаи выходное сопротивление будет равно
Z 2 = jω1C2 .
Подставим его в формулу входного сопротивления. Получим то, что входное сопротивление имеет индуктивный характер
Z1 = jω GC22 = jωL ,
где L — эквивалентная индуктивность
L = GC22 .
Рассмотрим модель последовательного колебательного контура с гиратором имитирующим катушку индуктивности (рис. 7).
Рис. 7 Резонансная частота такого контура вычисляется по следующей формуле
f0 |
= |
|
1 |
= |
|
G |
|
. |
|
2π |
LC |
2π |
C C |
2 |
|||||
|
|
|
|
||||||
|
|
|
1 |
|
|
1 |
|
Исследуем с помощью ЭВМ характеристики пассивного и активного последовательного колебательного контура.
4.1 Запуск программы схемотехнического моделирования Micro-Cap
Включить ЭВМ и запустить программу Micro-Cap
C:\MC9DEMO\mc9demo.exe или
ПУСК\Все программы\Micro-Cap Evaluation 9\Micro-Cap Evaluation 9.
В появившемся окне Micro-Cap 9.0.3.0 Evaluation Version (рис. 8) собрать схему для исследования колебательного контура (рис. 1).
8
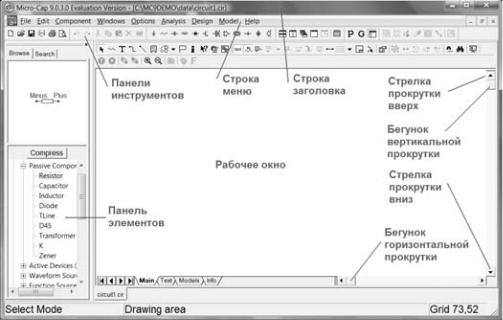
Рис. 8
4.2 Сборка схемы пассивного последовательного колебательного контура
Соберем схему пассивного последовательного колебательного контура (рис. 1).
4.2.1 Ввод источника синусоидального напряжения
Ввести источник синусоидального напряжения V1.
Откройте меню Component\Analog Primitives\Waveform Sources и выберите синусои-
дальный источник Sine Source (рис. 9).
9
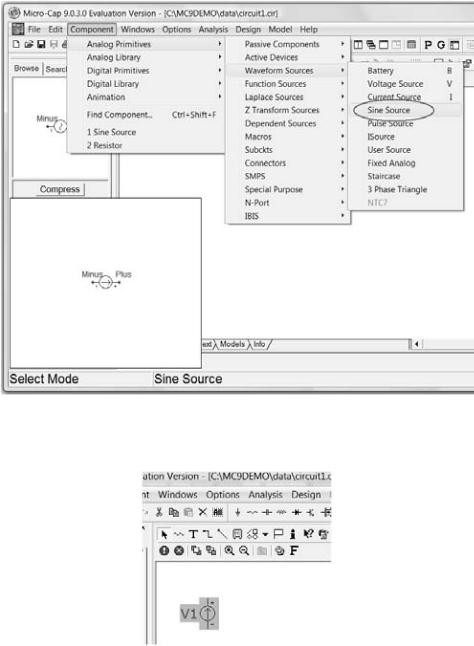
Рис. 9
Курсор примет форму графического изображения источника напряжения. Поместите его на рабочее окно так, как показано на рис. 10.
Рис. 10
Зафиксируйте это положение, щелкнув левой клавишей мыши. Появиться окно Sine Source. Введите 1V в окне Value, в окне Show установите галочку, в окне F частоту 8k, в окне RS внутреннее сопротивление источника 0 (рис. 11).
10
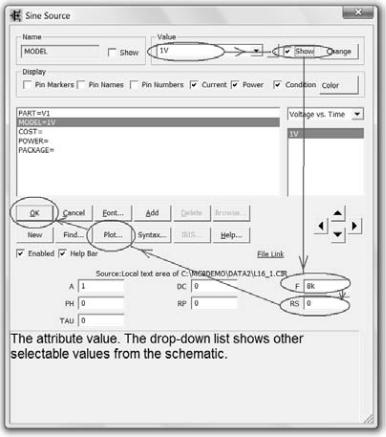
Рис. 11
Убедитесь, что источник правильно работает. Щелкните мышкой на кнопке Plot. Появиться окно Plot с зависимостью напряжения источника от времени (рис. 12).
11
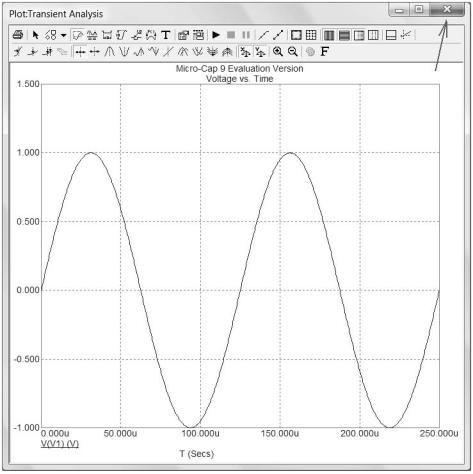
Рис. 12
Закройте это окно, щелкнув на кнопке Закрыть (рис. 12). Нажмите кнопку ОК (рис. 11).
4.2.2 Ввод земли
Откройте меню Component\Analog Primitives\Connectors и выберите землю Ground
(рис. 13).
12
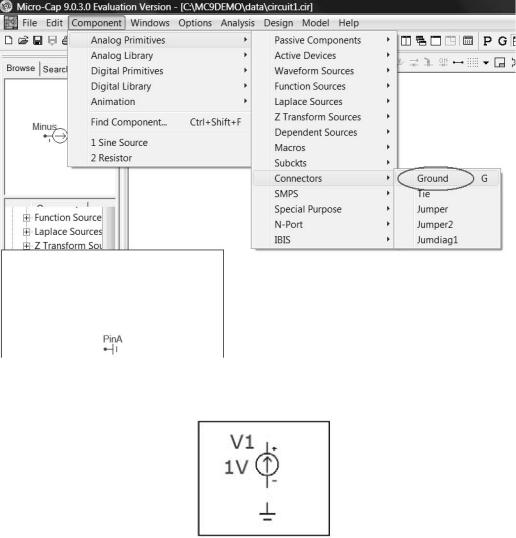
Рис. 13
Установите землю снизу от источника V1 (рис. 14).
Рис. 14
4.2.3 Ввод резистора
Ввести резистор R1.
Откроите меню Component\Analog Primitives\Passive Components и выберите команду резистор Resistor (рис. 15).
13
