
Frisk_2_16_17_23
.pdf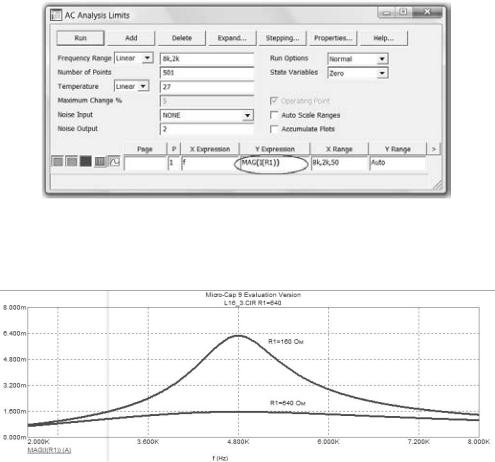
Данные графики занесите в соответствующий раздел отчета.
В случае возникновения проблем загрузите с сайта поддержки учебного процесса
(http://frisk.newmail.ru/) для ознакомления файл L16_2.CIR (File\Open…).
4.3.3 Построение зависимости модуля входного тока от частоты
Построить график резонансной кривой, т.е. зависимость модуля входного тока |I(f)| MAG(I(R1)) от частоты. Для этого нажмите клавишу F9 и в поле Y Expression введите
MAG(I(R1)) (рис. 36).
Рис. 36
Запустите построение, нажав кнопку OK.
На экране появиться два графика зависимости модуля входного тока от частоты при различных сопротивлениях (рис. 37).
Рис. 37
По полученным графикам определить величину добротности Q, нижнюю граничную частоту f1, верхнюю граничную частоту f2, абсолютную полосу пропускания П и модуль входного тока при резонансе I0.
Данные графики занесите в соответствующий раздел отчета, а полученные величины в таблицу 1.
Аналогичным образом построить зависимости модуля входного тока (R1=160 Ом):
•при двух значениях индуктивности L1=L и L1=2L;
•при двух значениях ёмкости C1=С и C1=2С.
Данные графики занесите в соответствующий раздел отчета.
24
4.3.4Построение зависимости модуля входного тока от частоты в схеме
сгиратором
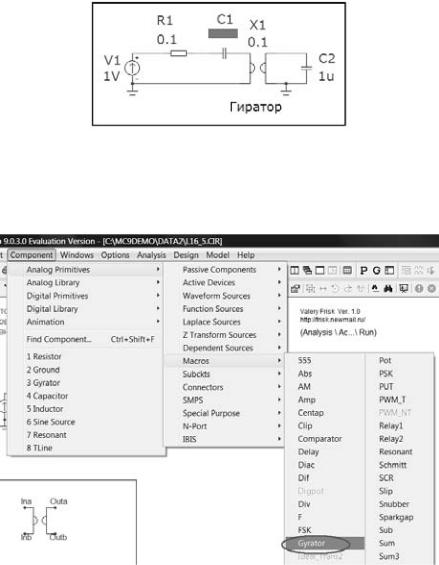
Вернитесь к исходной схеме, нажав на клавиатуре клавишу F3. С помощью мышки и клавиатуры введите схему активного колебательного контура с гиратором.
Рис. 38
Под С1 появиться введенные вами величина ёмкости рассчитанная в предварительном расчете (#3.6).
Для ввода гиратора откроите меню Component\Analog Primitives\Macros и выберите команду гиратор Gyrator (рис. 39).
Рис. 39
Построить график резонансной кривой, т.е. зависимость модуля входного тока |I(f)| MAG(I(R1)) от частоты. Для этого в меню Analysis выберите команду частотного анализа AC…(рис. 26). На экране появиться окно АС Analysis Limits, в котором задайте параметры построения требуемого графика так, как показано на рис. 40.
25
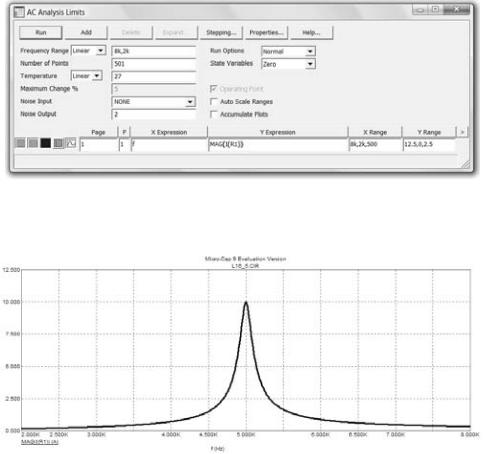
Рис. 40
Запустите построение, нажав кнопку OK.
На экране появиться график зависимости модуля входного тока от частоты (рис. 41).
Рис. 41
Отметьте на оси частот резонансную частоту f0 и занесите её величину в таблицу 1. Данный график занесите в соответствующий раздел отчета.
Повторите этот машинный эксперименты для R=0,2 Ом. Для чего вернитесь к исходной схеме, нажав на клавиатуре клавишу F3. С помощью мышки и клавиатуры измените значение сопротивления R1 с 0.1 на 0.2.
5 Обработка результатов машинного эксперимента
Сравнить полученные графики и данные с графиками и данными, полученными в предварительном расчете. Сделать выводы по каждому машинному эксперименту.
6 Вопросы для самопроверки
1.Почему резонанс в последовательном пассивном колебательном контуре называется резонансом напряжений?
2.Как рассчитывается резонансная частота сложного пассивного колебательного контура и как она рассчитывается для схем содержащих гиратор?
3.Что такое добротность последовательного пассивного колебательного контура?
26
4.Что такое полоса пропускания последовательного пассивного колебательного контура? Какие существуют способы расчета полосы пропускания?
5.Выведите уравнения, с помощью которых рассчитывают входные АЧХ и ФЧХ последовательного пассивного колебательного контура.
7 Содержание отчета
Отчет оформляется в формате MS Word. Шрифт Times New Roman 14, полуторный интервал.
Для защиты лабораторной работы отчет должен содержать следующий материал: титульный лист; цель работы; результаты машинного эксперимента; графики исследуемых зависимостей; выводы. К отчету должны быть приложены в напечатанном виде вопросы для самопроверки и ответы на них.
8Литература
1.Фриск В.В. Основы теории цепей. –М.: РадиоСофт, 2002. –288 с.
2.Бакалов В.П., Дмитриков В.Ф., Крук Б.И. Основы теории цепей. –М.: Радио и связь, 2003. –592 с.
3.Смирнов Н.И., Ганин В.И., Коробицына Н.М, Третьякова Т.В. Расчет характеристик частотоно-избирательных цепей. –М.: МИС, 1998. –51 с.
4.Асеев Б.П. Колебательные цепи. –М.: Связьиздат, 1955. –463 с.
5.Гаврилов Л.П., Соснин Д.А. Расчет и моделирование линейных электрических цепей с применением ПК. –М.: СОЛОН-Пресс, 2004. –448 с.
27
Лабораторная работа № 17
Исследование на ЭВМ резонансных явлений в пассивном параллельном колебательном контуре
1 Цель работы
С помощью программы Micro-Cap получить входные и передаточные характеристики одиночного параллельного колебательного контура при различных добротностях.
2 Задание для самостоятельной подготовки
Изучить основные положения теории цепей о резонансе напряжений стр. 97-101 [1], стр. 121-128 [2], стр. 19-32 [3] и стр. 64-95 [4]. Выполнить предварительный расчет, письменно ответить на вопросы для самопроверки.
3 Предварительный расчет
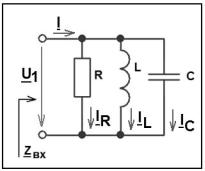
3.1 Рассчитать величину индуктивности L выбрав из заданного интервала величину ёмкости C [10; 40] нФ так, чтобы резонансная частота пассивного параллельного колебательного контура (рис. 1) fp=5 кГц.
Рис. 1
3.2 Рассчитать следующие параметры простого пассивного параллельного контура (R=14 кОм): ρ — характеристическое сопротивление;
Q — добротность;
f1 — нижнюю граничную частоту; f2 — верхнюю граничную частоту;
П — абсолютную полосу пропускания;
Z(fp) — модуль входного сопротивления при резонансе. Полученные данные записать в таблицу 1.
28
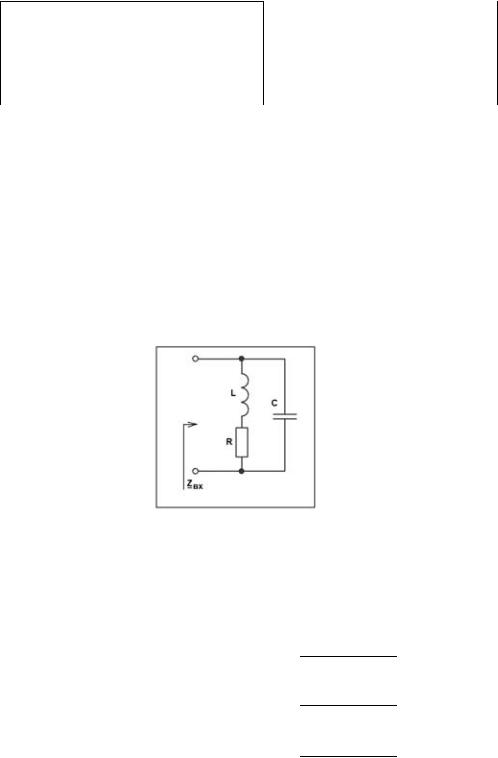
Таблица 1
По предварительному расчету Получено экспериментально
R=14 кОм, fp=5 кГц, С=_____ Ф, L=_____ Гн.
|
ρ,О |
Q |
f1, |
|
f2, |
|
П, |
Z(fp), |
f0, |
|
fp, |
Z(fp), |
f1, |
|
f2, |
|
П, |
Q |
||
|
м |
|
|
кГц |
кГц |
|
кГц |
Ом |
|
кГц |
Гц |
Ом |
кГц |
|
кГц |
|
кГц |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.3 |
Построить |
график |
зависимости |
модуля |
входного |
сопротивления |
|ZBX(f)| |
от частоты |
||||||||||||
f [2; 8] кГц.
3.4Построить график зависимости фазы входного сопротивления ϕZвх(f)=arg[ZBX(f)] от частоты f [2; 8] кГц.
3.5На одном графике построить четыре зависимости от частоты f [2; 8] кГц, U1=1 В:
•модуля входного тока |I(f)|;
•модуля тока в резисторе |IR(f)|;
•модуля тока в катушке |IL(f)|;
•модуля тока в конденсаторе |IС(f)|.
3.6Рассчитать следующие параметры пассивного параллельного контура первого типа (рис. 2)
для двух значений добротности Qp=2 и Qp=100 (L и С оставить прежними #3.1): R — сопротивление в ветви с катушкой индуктивности;
fp1 — резонансную частоту контура первого типа; Z(fp1) — модуль входного сопротивления при резонансе. Полученные данные записать в таблицу 2.
Рис. 2
Построить для двух значений добротности графики зависимости модуля входного сопротивления |ZBX(f)| и фазы входного сопротивления ϕZвх(f)=arg[ZBX(f)] от частоты f [2; 8] кГц.
Таблица 2
По предварительному расчету |
Получено экспериментально |
|||||
|
С=_____ Ф, L=_____ Гн. |
|
|
|||
|
|
|
|
|
|
Z(fp), |
Q |
|
R, |
fp1, |
Z(fp), |
fp1, |
|
|
|
Ом |
кГц |
кОм |
кГц |
кОм |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
29
4 Порядок выполнения работы
Простой пассивный параллельный колебательный контур состоит из конденсатора, катушки индуктивности и резистора (рис. 1).
Из условия резонанса тока, в параллельном пассивном колебательном контуре, записываемого в
виде
Im(Y BX ) = 0 ,
где комплексная входная проводимость контура равна
|
1 |
|
|
1 |
|
|
Y BX = |
|
+ j |
ωC − |
|
|
, |
R |
|
|||||
|
|
|
ωL |
|
||
можно найти резонансную частоту контура
Im(Y BX ) =ωpC −ω1L = 0 ,
p
ωp = LC1 ,
итак как
ωp = 2π f p ,
окончательно получим f p = 2π 1LC .
Остальные параметры простого последовательного контура вычисляются по следующим форму-
лам.
Характеристическое сопротивление
ρ = CL .
Добротность
Q = Rρ = ∏f p .
Нижняя граничная частота
ω1 |
= − |
1 |
|
+ |
|
|
1 2 |
+ |
1 |
|
, |
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
2RC |
|
|
LC |
||||||||||||||
|
|
|
|
|
|
2RC |
|
|
|||||||||
f |
|
= |
ω1 . |
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
2π |
|
|
|
|
|
|
|
|
|
|
|
||||
Верхняя граничная частота |
|
|
|
|
|||||||||||||
ω2 |
= − |
1 |
|
+ |
|
|
1 2 |
+ |
1 |
|
, |
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2RC |
|
|
|
|
LC |
|||||||||||
|
|
|
|
|
|
|
|
2RC |
|
|
|
||||||
f |
2 |
= |
ω2 . |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
||||
Абсолютная полоса пропускания П=f2-f1.
30
Комплексное входное сопротивление
Z BX = |
|
|
1 |
|
|
= Z (ω)e jϕ(ω) . |
1 |
|
|
1 |
|||
|
|
+ j |
ωC − |
|
|
|
|
R |
|
|
|||
|
|
|
ωL |
|
||
Модуль входного сопротивления при условии, что меняется только частота источника напряже-
ния
Z (ω) = |
|
|
|
|
1 |
|
|
. |
|
1 2 |
|
|
|
||||
|
|
|
|
1 2 |
||||
|
|
|
|
+ |
ωC − |
|
|
|
|
|
|||||||
|
|
R |
|
|
ωL |
|||
Фаза входного сопротивления в градусах
ϕ (ω) = −180π arctg
Комплексные токи
I = |
|
U |
1 |
,I R = |
U |
1 |
,I |
|
|
|
|||||||
Z BX |
||||||||
|
|
R |
|
|||||
|
ωC − |
|
1 |
|
|||||
|
|
|
R . |
||||||
|
|
||||||||
|
|
|
|
|
ωL |
|
|||
L = |
|
U |
1 |
|
,I C = |
U1 |
|||
jωL |
− j |
. |
|||||||
ωC
Определение добротности по резонансной кривой
Добротность Q последовательного контура можно определить при помощи резонансной кривой по формуле
Q = |
|
|
f p |
|
|
|
|
. |
|
f |
2 |
− f |
||
|
|
1 |
|
|
Необходимые для этого построения показаны на рис. 3.
Рис. 3
Для контура первого типа (рис. 2) значения индуктивности катушки и ёмкости конденсатора оставим прежними. Зададимся величиной добротности Qp. В этом случаи величина сопротивления вычисляется по формуле
L
R = p = C .
Qp Qp
Резонансная частота такого контура вычисляется по следующей формуле
ω |
p |
= |
1 |
1− |
R2 |
, |
|
LC |
ρ2 |
||||||
|
|
|
|
f p1 = ωπp .
2
31
Комплексное входное сопротивление может быть записано в виде
|
(R + jωL) |
− j |
|
|||
Z BX = |
ωC |
. |
||||
|
|
|||||
|
|
|
||||
|
|
1 |
||||
|
R + j |
ωL − |
|
|
||
|
|
|||||
|
|
|
ωC |
|||
Модуль входного сопротивления при резонансе можно вычислить по следующей формуле
Z ( f p1 ) = RQ2 .
Исследуем с помощью ЭВМ характеристики пассивного параллельного колебательного контура.
4.1 Запуск программы схемотехнического моделирования Micro-Cap
Включить ЭВМ и запустить программу Micro-Cap
C:\MC9DEMO\mc9demo.exe или
ПУСК\Все программы\Micro-Cap Evaluation 9\Micro-Cap Evaluation 9.
В появившемся окне Micro-Cap 9.0.3.0 Evaluation Version (рис. 4) собрать схему для исследования колебательного контура (рис. 1).
Рис. 4
4.2 Сборка схемы пассивного параллельного колебательного контура
Соберем схему простого пассивного параллельного колебательного контура (рис. 1).
4.2.1 Ввод источника синусоидального напряжения
Ввести источник синусоидального напряжения V1.
32
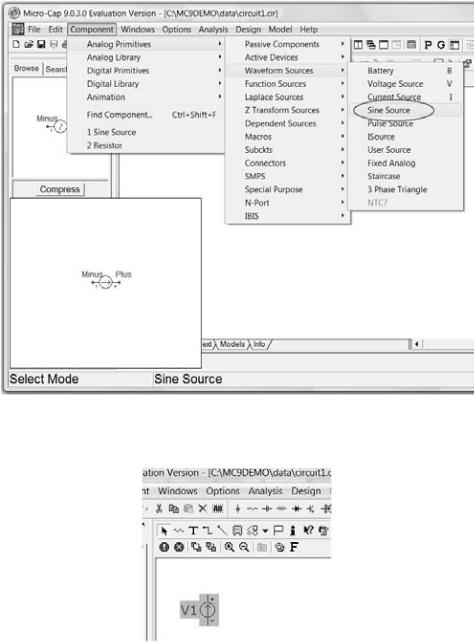
Откройте меню Component\Analog Primitives\Waveform Sources и выберите синусоидальный источник Sine Source (рис. 5).
Рис. 5
Курсор примет форму графического изображения источника напряжения. Поместите его на рабочее окно так, как показано на рис. 6.
Рис. 6
Зафиксируйте это положение, щелкнув левой клавишей мыши. Появиться окно Sine Source. Введите 1V в окне Value, в окне Show установите галочку, в окне F частоту 8k, в окне RS внутреннее сопротивление источника 0,001 Ом (1m) (рис. 7).
33
