Вопрос 9.

• Случайная величина –это величина, которая в результате опыта принимает то или иное значение ,при чем не известно заранее какое именно.

• С.В х имеет дискретное распределение если сущ.конечное или счетный набор чисел таких что

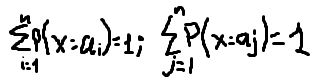
закон дискрет.распределения:

Дискретное распределение удобно задавать таблицей:

Х	а1	а2	…	an
Р	Р1	Р2	…	Pn

Рi= P(x=ai), i=1,n сумма вероятностей =1.

Случ.вел. х имеет непрерывное распределение если существует неотрицательная функция f(x), такая что для любого промежутка (а,в) числовой прямой

Р(х(а,в))=

f(x)-плотность распределения.

Она должна удовлетворять:

1.f(x)>=0

2.

Вопрос 10.

Функцией распределения случайной величины Х называют функцию F(x), определяющую для каждого значения х, вероятность того, что случайная величина Х примет значение меньше х, т.е.

F(x) = P (X <x).

Функция распределения обладает следующими свойствами:

1. Значение функции распределения принадлежит отрезку [0,1]: 0 ≤ F(x) ≤ 1.

2. Функции распределения есть неубывающая функция, х1<x2.F(x1)<=F(x2).

3. Вероятность того, что случайная величина Х примет значение, заключенное в интервале (а, b), равна приращению функции распределения на этом интервале:

Р(а < X < b) = F(b) – F(а). (2.1)

4. Если все возможные значения случайной величины Х принадлежат интервалу (а, b), то

F(x) = 0 при х ≤ а; F(x) = 1 при х ≥ b.

5. Справедливы следующие предельные отношения

Вероятность попадания случайной величины на заданном участке.

Для определенности условимся левый конец α включать в участок (α, β), а правый нет: α ≤ Х < β.

Выразим вероятность этого события через функцию распределения величины Х. Для этого рассмотрим три события:

событие А, состоящее в том, что X < β;

событие В, состоящее в том, что X < α;

событие С, состоящее в том, что α ≤ Х < β.

Событие А по теореме сложения вероятностей равно А = В + С и его вероятность Р(А) = Р(В) + Р(С) или P(X < β) = P(X < α) + P (α ≤ Х < β). Но вероятность нахождения случайной величины левее некоторой текущей переменной есть ни что иное, как функция распределения:

F(β) = F(α) + P (α ≤ Х < β) откуда

P (α ≤ Х < β) = F(β) - F(α)т.е. вероятность попадания случайной величины на заданный участок равна приращению функции распределении на этом участке. Будем неограниченно уменьшать участок (α, β), полагая, что β→α. В пределе вместо вероятности попадания на участок получим вероятность того, что величина примет отдельно взятое значение α:P(X=α) = limβ→α P(α ≤ Х < β) = limβ→α [F(β) - F(α)]

?11.Плотность распределения случайной величины. Свойства. Вероятность попадания случайной величины на заданный участок.

Случайную величину Х называют непрерывной (непрерывно распределенной) величиной, если существует такая неотрицательная функция p(t), определенная на всей числовой оси, что для всех х функция распределения случайной величины F(x) равна:

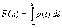. (6.7)

При этом функция p(t) называется плотностью распределения вероятностей непрерывной случайной величины.(f(x)) Если такой функции p(t) не существует, то Х не является непрерывно распределенной случайной величиной. Таким образом, зная плотность распределения, по формуле (6.7) можно легко найти функцию распределения F(x). И, наоборот, по известной функции распределения можно восстановить плотность распределения. Значит, наряду с функцией распределения, плотность распределения вероятностей непрерывной случайной величины задает ее закон распределения.

1.    Плотность распределения – неотрицательная функция:p(t)³0.

Геометрически это означает, что график плотности распределения расположен либо выше оси Ох, либо на этой оси.

2.    =1.

3. P(a<x<b)=F(b)-F(a) -Вероятность попадания случайной величины на заданный участок???

12. Числовые характеристики случайной величины. Центральные моменты. Дисперсия.

Математическое ожидание – среднее значение случайной величины. Сумма произведении всех возможных значений с.в. на вероятности этих значений. Центральный момент первого порядка 1.Математическое ожидание постоянной величины равно ей самой: M[C]=C, C – постоянная;

2. M[C•X]=C•M[X]

3. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий: M[X+Y]=M[X]+M[Y] 4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий: M[X•Y]=M[X]•M[Y], если X и Y независимы. Для непрерывной сл. величины, заданной функцией плотности вероят­ности f(x), математическое ожидание определяется в виде интеграла

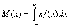
Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. Второй центральный момент с.в. Х

D(X)=M(X²)-M²(X) для непрерывной случайной величины 

Свойства: 1.D[C]=0, C – постоянная;

2. D[C•X]=C²•D[X]

3. D[X+Y]=D[X]+D[Y] 4. D[X-Y]=D[X]-D[Y]

5. D[X]0

Дисперсия числа появлений в n независимых испытаниях (с одинаковой вероятностью р появления события в каждом испытании и вероятностью не появления события q вычисляется по формуле

  D(X) = n*p*q

Средний квадрат отклонения с.в.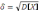

Число, M[X-M[X^k]], центральный момент порядка k с.в. Х