
- •1Вопрос.
- •2Вопрос.
- •3. Действия над событиями. Сложение событий. Сложные события.
- •4. Теорема сложения вероятностей. Следствия.
- •Вопрос 5.
- •Вопрос 6.Формула полной вероятности:
- •7. Формула Байеса
- •Вопрос 9.
- •Вопрос 10.
- •Вопрос 13.Характеристики случайной величины: центральный момент и дисперсия
- •Вопрос14.
- •15. Законы распределения – равномерный, показательный.
- •Вопрос 17:
- •Вопрос 18.Числовые характеристики системы двух случайных величин. Начальные, центральные моменты.
- •1,1-Называет ковариацией и обозначают cou(x1;x2).
- •19. Корреляционный момент. Коэффициент корреляции.
- •20. Уравнение линейной регрессии. Коэффициент линейной регрессии.
- •Вопрос 21.
- •Вопрос 22.
1Вопрос.
Событие- это факт который в результате опыта может произойти или нет.
Непосредственные исходы событий называются элементарные события и обозначаются W.
События называются достоверными, если оно обязательно наступит.
Событие называется невозможным, если оно заведомо не произойдет.
Два события называются - не совместны, если появление одного из них исключает появление другого в одном опыте.
Событие образует полную группу событий, если они попарно не совместны, и в результате опыта происходит одно и только из них.
Классическая схема вычисления вероятности:
Происходит опыт с n- исходами, которые можно представить в виде полной группы событий не совместных равновозможных событий.
Такие исходы называются случайными элементарными событиями.
Случай W который приведет к наступлению к А называется благоприятным событию А.
Вероятность события А называется число m-благоприятных событию А к общему числу n.
![]()
Из классической ОП! вероятности следует 0<=P<=1
0-невозможно
1-достоверность
2Вопрос.
Относительной частотой события А (Р*(А)) в серии nопытах называется
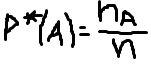
0<=P*(A)<=1
Статистической вероятностью события А называется число около которого калеблица относительная частота события А при достаточном большом числе испытаний.
Р*(А)приблизительна равна Р(А).
3. Действия над событиями. Сложение событий. Сложные события.
Событие – факт, который в результате опыта может произойти или не произойти.
Сумма
(объединение) событий представляет
собой сложное событие, состоящее в
появлении хотя бы одного из событий А
и В. Объединение событий обозначается
как
 ,
или
,
или .
Событие
C произведением A и B, если оно состоит
из всех элементарных событий, входящих
и в A, и в B.
Разностью событий A-B называется
событие C, состоящее из всех элементарных
событий, входящих в A, но не входящих в
B.
.
Событие
C произведением A и B, если оно состоит
из всех элементарных событий, входящих
и в A, и в B.
Разностью событий A-B называется
событие C, состоящее из всех элементарных
событий, входящих в A, но не входящих в
B.
События A и B называются несовместными, если они никогда не могут произойти в результате одного испытания.
Противоположным
событием А, называется событие 
 ,
которое происходит, когда не происходит
А
,
которое происходит, когда не происходит
А
4. Теорема сложения вероятностей. Следствия.
Теорема
(сложения
вероятностей).Вероятность
суммы двух несовместных событий равна
сумме вероятностей этих событий.![]()
Говорят, что несколько событий в данном опыте образуют полную группу событий, если в результате опыта непременно должно появиться хотя бы одно из них.
Следствие
1:Если
события
![]() образуют
полную группу несовместных событий, то
сумма их вероятностей равна единице.
образуют
полную группу несовместных событий, то
сумма их вероятностей равна единице.![]()
Определение.Противоположныминазываются два несовместных события,
образующие полную группу.Следствие
2:Сумма
вероятностей противоположных событий
равна единице.![]()
Вопрос 5.
Условной вероятностью события В при условии что произошло событие А называется отношение произведение события к вероятности события А.

Теорема умножения вероятности:
Р(А*В)=Р(В/А)*Р(А)=Р(А/В)*Р(В)
вероятность двух событий равна произведению условной вероятности одного из них на безусловную вероятность другого.
Р(А*В*С)=Р(В/А)*Р(А)*Р(С/АВ)
![]()
Событие А и В называются независимыми если Р(А*В)=Р(А)*Р(В)
Событие А независимо от В если его условная вероятность равна безусловной.
Р(ф/В)=Р(А).
