
ТЕМА 4.2 Передача и преобразование сигналов нелинейными цепями
Содержание |
|
Трансформация спектров колебаний нелинейными элементами. |
........................... 1 |
Общая схема нелинейных преобразований колебаний ............................................ |
5 |
Умножение частоты...................................................................................................... |
6 |
Выпрямление переменного тока................................................................................. |
8 |
Амплитудная модуляция............................................................................................ |
11 |
Детектирование АМ – колебаний ............................................................................. |
14 |
Преобразование частоты............................................................................................ |
18 |
Трансформация спектров колебаний нелинейными элементами.
Ранее было установлено, что основным свойством НЭ является его способность трансформироватьспектр колебания. Необходимо выяснить, в каких соотношениях находятся гармонические составные выходного колебания (реакции цепи) с гармоническими составляющими входного воздействия и как влияет вид нелинейности рабочего участка характеристики НЭ на частотный состав выходного колебания.
Будем при анализе сходить из того, что характеристика НЭ аппроксимирована полиномом. Ограничимся рассмотрением трансформации спектров колебаний нелинейным сопротивлением. Положив для простоты
напряжение смещения u0 |
= 0 , ВАХ можно представить как |
|||||||
i(u) =α |
0 |
+α u +α |
u2 |
+... +α |
n |
un |
(13.1) |
|
|
1 |
2 |
|
|
. |
|||
Рассмотрим спектр тока на выходе нелинейного сопротивления для двух случаев:
на НЭ воздействует напряжение
u =Um cosωt ;
на НЭ воздействует два напряжение одновременно (бигармоническое воздействие), т.е. на его входе
u =Um1 cosω1t +Um2 cosω2t . (13.3)
Очевидно, что воздействие в виде суммы постоянного и гармонического
напряжений будет частным случаем второго воздействия, когда ω1 или ω2 равно нулю.
I. Спектр тока при гармоническом воздействии
Для определения спектра тока при гармоническом воздействии определим гармонический состав тока, вызываемого каждым слагаемым полинома (13.1).

При этом будем пользоваться обычными тригонометрическими преобразованиями.
Первое слагаемое дает ток α0 с нулевой частотой;
второе - α1u =α1Um cosωt ;
третье -α2u2 =α2Um2 cos2 ωt = α22Um2 + α22Um2 cos2ωt ;
четвертое - |
α u3 |
=α U 3 |
cos3 ωt = α3Um3 |
(1+cos2ωt)= |
|
3 |
3 m |
2 |
|
|
|
|
|
=α3U2 m3 cosωt + α3U2 m2 cosωt * cos2ωt =
=α3U2 m3 cosωt + α3U4 m3 cos3ωt + α3U4 m3 cosωt =
=34α3Um3 cosωt + 14α3Um3 cos3ωt;
пятое - |
α |
u4 |
=α U 4 |
cos4 |
ωt |
= |
3 |
α U 4 |
+ |
|||||
|
|
4 |
|
|
4 |
m |
|
|
|
|
8 |
4 |
m |
|
|
+ |
1 |
α U 4 |
cos2ωt |
+ |
1 |
α U 4 |
cos4ωt |
||||||
|
|
2 |
|
4 m |
|
|
|
8 |
|
4 |
m |
|
|
|
и т.д.
Из рассмотренного следует, что четные члены полинома (13.1) дают гармоники с частотами 0,2 ω , 4 ω , 6 ω и нечетные - с частотами ω , Зω , 5 ω и
.т.д.
Причем, К -ый член вызывает появление гармоник с частотами, не превосходящими к ω .
Просуммировав гармоники тока, вызываемые каждым членом аппроксимирующего полинома соответственно по частотам, получим ток.
i(u)= I0 |
+ Im1 cosωt + Im2 cos 2ωt +... + Imn cos nωt. (13.4) |
|||||||||||||||||||
Амплитуды каждой гармоники будут определяться: |
||||||||||||||||||||
I |
|
=α |
|
|
+ |
α |
|
U |
2 |
|
3 |
α U |
4 +..., |
|
||||||
|
|
|
|
|
|
m + |
8 |
|
||||||||||||
|
0 |
|
|
|
0 |
|
|
2 |
2 |
|
|
4 |
m |
|
||||||
I |
|
|
=α U |
|
+ |
3 |
α U 3 |
+ |
5 |
α U 5 |
+..., |
|||||||||
|
m1 |
|
|
|
|
1 |
m |
|
|
4 |
2 |
m |
|
8 |
5 m |
|
||||
I |
|
|
= |
1 |
|
α U |
2 |
+ 1 α U 4 |
+..., |
|
||||||||||
|
|
2 |
|
|
m |
|
||||||||||||||
|
m2 |
|
|
|
2 |
|
|
|
|
2 |
4 |
|
m |
|
|
|
||||
I |
|
|
= |
1 |
α U |
3 + |
|
5 |
α U 5 |
+.... |
|
|||||||||
|
|
4 |
|
|
|
|||||||||||||||
|
m3 |
|
|
|
3 |
|
m |
16 |
|
5 |
|
m |
|
|
|
|||||
И т.д.
Для К-ой гармоники амплитуда может быть определена из выражения
n−k |
|
(2ν + k)! |
|
|
Imk = ∑2 |
|
|
α2ν +kUm2ν +k , |
|
2 |
2ν +k −1 |
|||
y=0 |
ν!(ν + k)! |
(13.5) |
||
|
|
|
|
|
где α2ν +k - коэффициент аппроксимации.
Из приведенного расчета можно сделать вывода относительно спектрального состава тока, протекающего через нелинейное сопротивление при гармоническом воздействии:
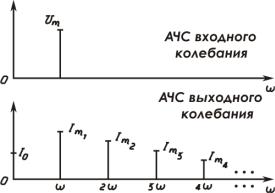
1.В спектре тока могут содержаться постоянная составляющая, колебание с частотой воздействия ω и высшие гармоники с частотами 2ω , 3ω и
т.д. (рис. 13.1).
2.Амплитуды всех гармоник тока являются нелинейными функциями
амплитуды внешнего воздействия U m
3.Амплитуды четных гармоник определяются всеми четными членами
аппроксимирующего полинома степени п , |
нечетных - всеми |
||
нечётными членами этого полинома. |
|
i(u)=i(−u), то |
|
4. |
Если характеристика НЭ четная, |
т.е. |
|
нечетные коэффициенты αk равны нулю.
В этом случае в спектре тока будут содержаться только четные гармоники. При нечетной характеристика четные гармоники обращаются в нуль.
Рис.13.1.
2. Спектр тока при бигармоническом воздействии; Выяснимсоставспектратокаприбигармоническомвоздействии,используя
обычные тригонометрические преобразования. Причем, наибольший интерес для нас будут представлять частоты гармоник, вызываемые каждым членом
аппроксимирующего полинома. Нулевой член дает значение тока α0 (частота ω - 0 ). Первый член α1u =α1U m1 cosω1t +α2U m2 cosω2t дает гармоники с частотами
ω1 и ω2 .
Второй член
α2u =α2Um21 cos2 ω1t +α2Um2 2 cos2 ω2t + 2α2U m1U m2 cosω1t cosω2t = = α22 (U m21 +U m2 2 )+ α22 U m21 cos 2ω2t + α22 U m2 cos 2ω2t +
+α2Um1Um2 cos(ω1 −ω2 )t +α2Um1U m2 cos(ω1 +ω2 )t
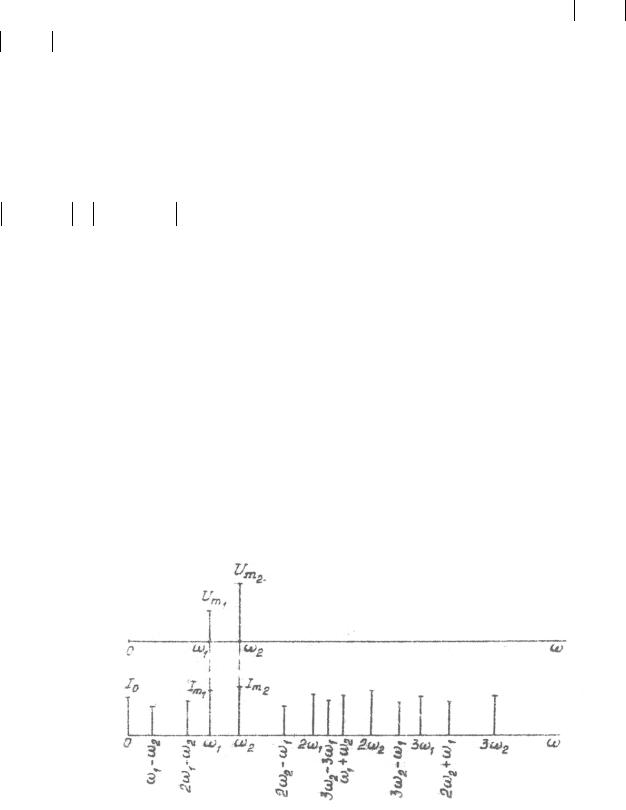
вызывает появление гармоник тока с частотами 0 , 2ω1 , 2ω2 , ω1 −ω2 и
ω1 +ω2 .
Аналогичным образом можно найти все слагаемые для третьего члена полинома, вызывающего появление гармоник тока с частотами
ω |
ω |
|
|
2ω1 ±ω2 |
|
ω1 ± 2ω2 |
|
3ω |
|
3ω |
|
|
|
|
|
|
|
|
|
||||||
1 , |
|
2 |
, |
|
, |
|
, |
1 |
, |
|
2 |
. Номер члена полинома |
определяет значение частот высших гармоник, им вызываемых. Четвертый член
|
2ω |
2ω |
|
|
ω1 |
±ω2 |
|
4ω |
4ω |
|
|
3ω1 |
±ω2 |
|
|
|
|
|
|
|
|
||||||||
ряда даст гармоники с частотами 0 , |
1 , |
|
2 |
, |
|
|
, |
1 , |
|
2 |
, |
|
|
, |
ω1 ±3ω2 , 2ω1 ± 2ω2 . Анализируя полученные выражения для частот, можно
заключить, что при бигармоническом воздействии с частотами ω1 и ω2 реакция НЭ содержит в общем случае гармонические составляющие комбинационных частот
|
pω1 ± qω2 |
|
, |
(13.6) |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|||
|
Где p = 0,1,2,…; |
q = 0,1,2,… . |
|
q = 0, называются |
|||
Частоты, получаемые в частном случае при p = 0 или |
|||||||
кратными частотами. Для К-го члена полинома должно быть |
p + q ≤ K . Сумма |
||||||
коэффициентов |
|
p + K называется |
порядком |
тока. |
Возникновение |
||
комбинационных частот показано на рис.13.2. Проведенный расчет позволяет сделать выводы относительно спектрального состава тона, протекающего через НЭ при бигармоническом воздействии.
Риc. 13.2
