

Основные свойства нелинейных цепей
Цепи, содержащие в своем составе нелинейные элементы, имени основные свойства:
Не подчиняются закону Ома (т.е. в выражениях
i = |
1 |
*u |
R(u) |
|
R(u) |
не является постоянной величиной для всех |
|||
|
|
, |
|
значений u).
2.Законы Кирхгофа (первый и второй) для нелинейных цепей выполняются полностью.
3.Способны изменять форму воздействующего колебания (рис.12.в,а). Со спектральной точка зрения нелинейные цепи могут осуществлять нелинейное преобразование (трансформацию) спектра, т.е. возникновение гармоник с частотами, которых нет в воздействующем колебании.
4.К ним неприменим принцип суперпозиции, что очень осложняет расчет, так как невозможно воспользоваться суперпозиционными методами анализа.
5.В некоторых отдельных случаях, когда характеристика НЭ имеет линейный участок, а амплитуда воздействующего колебаний небольшая, т.е. мгновенное значение воздействующего колебания не выходит за пределы этого участка, к нелинейной цепи возможно применить принцип суперпозиции (рис. 12.6,б).
Рис.12.6
Методы расчета нелинейных цепей
Так как нелинейные цепи не подчиняются принципу суперпозиции, то основным методом расчета здесь будет являться метод дифференциальных уравнений. Для получения систем уравнений, описывающих процессы в нелинейных цепях, используются законы Кирхгофа.
В качестве примера получим дифференциальное уравнение для цепи
(рис.12.7).

На основе второго закона Кирхгофа
получаем |
|
|
|
|
|
|
|||
uR (i) +uL (i) = e(i) , |
(12.1) |
|
|||||||
где |
|
uR (i) |
|
-BAX |
нелинейного |
||||
сопротивления. |
|
|
|
|
|||||
Напряжение |
|
на |
индуктивности |
||||||
выражается |
|
|
|
|
|
||||
|
dψ(i) |
|
dψ di |
|
|
Рис. 12.7 |
|||
uL = |
|
|
= |
|
|
= |
|
|
|
dt |
di |
dt |
|
|
|||||
|
|
|
|
|
|
||||
= L |
(i) di . |
|
|
|
|
|
|
||
d |
dt |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
Здесь ψ(i) - магнитная характеристика нелинейной индуктивности. |
||||||||
|
Тогда выражение (12.1) будет |
||||||||
|
L (i) di(t) |
+ R(i)i(t) = e(t) |
|
||||||
|
|
d |
dt |
|
|
. |
(12.2) |
||
|
|
|
|
|
|
||||
|
Порядок полученного дифференциального уравненияостался таким же, как |
||||||||
и для линейной RL цепи. Однако коэффициенты в нём не являются постоянным, |
|||||||||
зависят от |
|
тока |
i . |
Решение |
нелинейных дифференциальных уравнений |
||||
чрезвычайно сложно, и решаются, как правило, приближенно. Но даже и этом случае необходимо знать математические выражения для нелинейных коэффициентов, которые определяются статическими характеристиками НЭ и их динамическими параметрами.
Если в схеме цепи содержаться несколько однотипных НЭ, включенных параллельно или последовательно, то можно перейти к одному эквивалентному НЭ, сложив статические характеристики всех (рис. 12.8).
Разумеется, складывать характеристики НЭ необходимо в одном и том же масштабе. Результирующая характеристика используется в дальнейшем при расчёте.
Из аналитических методов методдифференциальных уравнений – наиболее общий для расчёта нелинейных цепей. Для различных конкретных случаев могут применяться и другие методы и приёмы расчета. Например, для цепей постоянного тока, где значения напряжений токов фиксированы, можно воспользоваться методам уравнений Кирхгофа или методом контурных токов.
В случае слабых сигналов, когда рабочий участок характеристики является линейным (см. рис. 12. 6, б), НЭ считают в пределах данного участка линейным и применяют обычные методы расчета.
Кроме аналитических, существует еще графические методы расчета. Они дают меньшую точность и, как правило, позволяют получать решение лишь для простых цепей. Графические метода не обладают общностью и при из менении параметров цепи или параметров внешнего воздействии весь расчет требуется выполнить заново.
Аналитические метода обладают общностью. Они обеспечивают более высокую точность и позволяют исследовать, цепи при сложных воздействиях. Однако для аналитического расчета необходимо знать аналитическое выражение характеристики НЭ, т.е. функцию, которой можно описать графически заданную характеристику. Такая функция называется аппроксимирующей.
Методы аппроксимации характеристик НЭ.
Аппроксимацией характеристики называется ее приближенное представление в виде некоторой математической функции. Аппроксимация характеристик НЭ, как правило, неоднозначна, т. е. может быть осуществлена различными математическими выражениями, физическая природа или тип НЭ при этом не играет никакой роли. Выбор метода аппроксимации зависит от:
назначения НЭ, форм характеристики, удобства анализа,
требуемой точности расчета, режима работы НЭ, определяемого рабочей точкой и рабочим участком
характеристики.
Вцелом, выбор наиболее подходящего выражения для аппроксимации характеристики - это дело не только математической техники, но и своего рода инженерное искусство, основанное на глубоком знании физических процессов в нелинейных цепях. Наиболее распространенными являются метода кусочнолинейной аппроксимации, аппроксимации степеням полиномом и кроме того, известны еще аппроксимации экспоненциальным полиномом и трансцендентными функциями.
Вдальнейшем будем рассматривать первые два метода. Они наиболее широко применяются при инженерных расчетах цепей, содержащих нелинейные элементы.
Метод кусочно-линейной аппроксимации.
При этом методе характеристика НЭ заменяется ломаной линией, составленной из прямолинейных отрезков (рис.12.9), в пределах которых НЭ можно рассматривать как линейный. Соответственно и расчет цепи с НЭ будет состоять из нескольких, связанных между собой расчетов линейных цепей.
Прямолинейные отрезки проводятся так, чтобы они удовлетворительно совпадали с действительной кривой. Характеристику (см. рис.12.9) можно аналитически записать, как:
i = 0 |
при u < u1 ; |
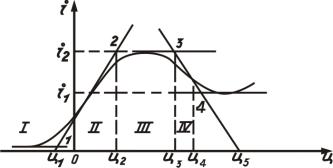
i = S1(u −u1) |
при |
u1 ≤ u < u2 ; |
|||||||
i = i |
2 |
|
|
при |
u2 |
≤u <u3 |
; |
||
|
|
|
|
|
|||||
i = S2 (u −u3 ) |
при |
u3 ≤u <u4 и т.д., |
|||||||
Где S1 = |
i2 |
|
|
|
|||||
u2 −u1 |
|
- крутизна участка II, |
|||||||
S2 = |
i2 |
−i4 |
|
|
|
||||
u3 |
−u4 |
- крутизна участка IV. |
|||||||
Рис.12.9.
Кусочно-линейная аппроксимация особенно проста и удобна для исследований и расчётов, когда основное значение имеет нижний изгиб характеристики, так как тогда можно ограничиться двумя прямыми (участки I и II). Для этого случая хорошо разработан метод расчёта в зависимости от одного параметра, положения точки перехода от одного аппроксимирующего отрезка к другому (точка I ,см.рис.12.9). Этот метод, разработанный советским учёным, академиком Бергом А.И., рассмотрим на примере ВАХ нелинейного сопротивления – лампового триода (рис.12.10).
К нелинейному сопротивлению подведено напряжение смещение U0 и
косинусоидальное напряжение с амплитудой Um
u =U0 +Um cos Ωt. (12.3)
Напряжение и ток изображены в зависимости от полной фазы Ωt в градусах
(см.рис.12.10).
При выбранных значениях U0 и Um ток i имеет форму отдельных косинусоидальных импульсов. Половина длительности импульса тока,
выраженная в градусах, называется углом отсечкиθ .
Очевидно, что θ может изменяться в пределах от нуля до 180 градусов.

Рис.12.10.
Найдём аналитическое выражение для тока i . При u <U0 , i =0 ;
u >U0 , i = S(u −U3 ), где S - крутизна аппроксимирующей прямой, U3 - напряжение запирания лампы.
Подставив значение u из выражение (12.3) в формулу (12.4), получим для
u >U0
i = S(U0 +Um cos Ωt −U3 ) . |
(12.5) |
Если Ωt=0 , то ток i = 0 , следовательно, |
|
S(U0 +Um cosθ −U3 ) = 0 . |
(12.6) |
Откуда |
|
cosθ = U3 −U0 |
|
Um . |
(12.7) |
Угол отсечки θ однозначно определяется, если известны напряжение
смещения U0 , напряжение запирания U3 и амплитуда переменного напряжения
Um .
Вычтем из (12.5) выражение (12.6). Получим
i = SUm (cos Ωt −cos Ω). |
(12.8) |
При Ωt = 0 получим максимальное значение тока |
|
Imax = SUm (1−cosθ). |
(12.8) |
Заметим, что ток i представляет собой периодическую функцию времени.
Следовательно, его можно представить в виде спектра. Амплитуда К –ой гармоники

|
|
|
T |
|
|
|
π |
|
|
||
|
|
2 |
2 |
−ikΩt |
|
2π |
2 |
−ikΩt |
|
||
Imk |
= |
|
|
i(t)e |
|
dt = |
|
|
i(t)e |
|
dt = |
T |
|
|
|
|
|
||||||
|
|
∫T |
|
|
πT ∫π |
|
|
||||
|
|
|
− |
2 |
|
|
|
− |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
=1 π∫i(Ωt)e−ikΩt dΩt
π−π
Так как ток-функция четная (косинусоидальные импульсы), то
Imk |
= |
|
2 |
|
π∫i(Ωt)cosπΩtdΩt = |
2 |
θ∫i(Ωt)cosπΩtdΩt. |
|
|||||||
π |
π |
(12.10) |
|||||||||||||
|
|
|
0 |
|
|
|
0 |
|
|||||||
Постоянная составляющая |
|
|
|||||||||||||
I0 = |
1 |
π∫i(Ωt)dΩt = |
1 |
θ∫i(Ωt)dΩt. |
|
|
|||||||||
π |
π |
|
(12.11) |
||||||||||||
|
|
|
0 |
|
|
|
0 |
|
|
|
|||||
Подставив в выражения (12.10) и (12.11) значение тока (12.8) и произведя |
|||||||||||||||
соответствующие вычисления, получим |
|
|
|||||||||||||
I0 |
= |
|
S Um |
|
(sinθ −θ cosθ); |
|
|
||||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
π |
|
|
|
|
|
|
|||
Im1 |
= |
|
|
S Um |
(θ −sinθ cosθ). |
|
|
||||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
π |
|
|
|
|
|
|
|||
Для К>1 |
|
|
|
|
|
|
|||||||||
Imk |
= |
|
2S Um |
sin kθ cosθ −k coskθsinθ |
|
|
|||||||||
|
|
|
|
||||||||||||
|
|
|
|
|
|
π |
|
k(k2 −1) |
. |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Разделив амплитуды гармоник на максимальное значение тока выражение (12.9), получим нормированные амплитуды гармоник, которые называются коэффициентами Берга.
α |
0 |
= |
|
I0 |
= sinθ −θ cosθ |
||||||||
|
Imax |
||||||||||||
|
|
|
|
|
|
π(1−cosθ) |
|||||||
|
|
|
|
|
|
|
|||||||
α1 |
= |
|
Im1 |
|
= |
θ −sinθ cosθ |
, |
|
|||||
Imax |
|
π(1−cosθ) |
|||||||||||
|
|
|
|
|
(12.12) |
|
|||||||
αk |
= |
|
Imk |
|
= |
2 |
|
|
sin kθ −k cos kθ sinθ |
. |
|||
|
|
|
|
|
|
|
|||||||
|
Imax |
|
π |
||||||||||
|
|
|
|
|
|
|
|
k(k 2 −1)(1−cosθ) |
|||||
k >1
Коэффициенты Берга зависят только от угла отсечки. Примерный вид зависимости изображён на рис.12.11. Коэффициенты Берга табулированы и имеются во многих книгах и справочниках.
