
TsOS_VOPROSY_1
.docxПримеры задач к экзамену
по дисциплине
«Цифровая обработка сигналов»
Вычислите значения
 и
и
 на выходе графа «бабочка» (см. ниже).
на выходе графа «бабочка» (см. ниже).
Дано:
 ,
,
 ,
,
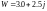

Дана передаточная функция линейной дискретной системы (ЛДС) в форме
 .
Определите порядок ЛДС.
.
Определите порядок ЛДС.
Порядок ЛДС определяется по максимальной степени передаточной функции, в данном случае порядок ЛДС = 8
Дано разностное уравнение линейной дискретной системы (ЛДС) в форме
 .
Определите порядок ЛДС.
.
Определите порядок ЛДС.
Из уравнения видно, что у нас присутствуют задержанные максимум на 4 такта входные сигналы.
Значит и порядок фильтра = 4.
Дано разностное уравнение линейной дискретной системы (ЛДС) в форме
 .
Нарисуйте структуру ЛДС.
.
Нарисуйте структуру ЛДС.

Дана передаточная функция линейной дискретной системы (ЛДС) в форме . Нарисуйте структуру ЛДС.

Даны значения нулей и полюсов линейной дискретной системы (ЛДС). Определить является ли ЛДС устойчивой?
Нули:
 ,
,

Полюсы:
 ,
,
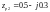
строишь единичную окружность и там откладываешь действительную часть по оси Х, а мнимую по оси Y, если точка выходит за окружность, то ЛДС не устойчива
для устойчивости нас интересуют только Полюсы по идее можно просто взять 0.5^2 + 0.3^2 -> если больше 1, то не устойчива
Дано разностное уравнение линейной дискретной системы (ЛДС) в форме
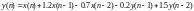 .
Задано воздействие на входе ЛДС в форме
.
Задано воздействие на входе ЛДС в форме
 для
для
 и
и
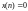 для
для
 и
и
 .
Найдите отклик системы
.
Найдите отклик системы
 для
для
 ,
т.е.
,
т.е.
 .
.
Просто подставляем и считаем y(0), y(1), y(2)
y(0) = x(0) + 1.2x(-1) - 0.7*x(-2) - 0.2y(-1) + 1.5y(-2) = 0.5
y(1) = x(1) + 1.2x(0) - 0.7*x(-1) - 0.2y(0) + 1.5y(-1) = 1 + 0.6 - 0.25 = 1.35
y(2) = x(2) + 1.2x(1) - 0.7*x(0) - 0.2y(1) + 1.5y(0) = 0.5 + 1.2 – 0.35 – 0.675 + 0.75 = 2.45 – 1.1 = 1.35
Дана импульсная характеристика линейной дискретной системы (ЛДС) в форме
 .
Задано воздействие на ЛДС в форме
.
Задано воздействие на ЛДС в форме
 для
и
для
и
.
Найдите отклик системы для
и для
для
и
для
и
.
Найдите отклик системы для
и для
 ,
т.е.
и
,
т.е.
и
 .
.
y(2) = x(0)*h(2) + x(1)*h(1) + x(2)*h(0) = 0.3 * 0,5 + 0.7 * 0.9 + 0.7 * 1 = 1.48
y(5) = x(0)*h(5) + x(1)*h(4) + x(2)*h(3) + x(3)*h(2) = 0.3*0 + 0.7*0 + 0.7*0.5 + 0.3*0.9 = 0.62
Задана верхняя частота спектра сигнала Fв = 2750 Гц. Найдите максимально возможный интервал дискретизации, при котором условия теоремы Котельникова еще будут выполняться.
Fд = 2*Fв = 2*2750 = 5500 Гц – посчитали минимальную частоту дискретизации
Tд = 1/5500 = 0.18 мс – посчитали максимальный интервал дискретизации
Дана последовательность в форме
 для
для
 и
для
и
и
для
и
 .
По формуле вычисления прямого дискретного
преобразования Фурье вычислите значение
коэффициента
.
По формуле вычисления прямого дискретного
преобразования Фурье вычислите значение
коэффициента
 для
для
 .
.
Задана передаточная функция КИХ-фильтра в форме
 .
Найдите отсчеты импульсной характеристики
фильтра.
.
Найдите отсчеты импульсной характеристики
фильтра.
h(n) = b(0) * δ(n) + b(1)* δ(n-1)…..b(N)* δ(n-N) - функция Дирака ( Импульсная функция ), которая равна 1,
при n = 0, и 0 во всех остальных случаях, т.е. отсчеты ИХ будут равны h(n)=b(n), т.е. 1 , 0.2 , 0.3, 0, 0, 0. 0.6 , 0, -0.8
Двоичный код на выходе АЦП имеет вид: 111001, 100100, 101110, … Сколько уровней квантования используется при квантовании сигналов?
Уровни квантования можно посчитать возведя двойку в степень, равную разряду двоичного кода ( в данном случае 6 ), тогда уровень квантования = 64.

Вот для примера как выглядели бы уровни квантования, если бы их было 6.
На рисунке приведен график дискретного сигнала. Найти значение частоты дискретизации.

"На данном графике мы видим отсчеты дискретного сигнала, очевидно они взяты с интервалом дискретизации 0.04 мс, остается посчитать по формуле частоты 1/0.00004 = 25000 Гц”
