
Лабораторная работа №108. Определение показателя преломления жидкости при помощи рефрактометра ИРФ-24
.doc
МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ДИЗАЙНА и ТЕХНОЛОГИИ
Методические указания к лабораторной работе №108
“Определение показателя преломления жидкости
при помощи рефрактометра ИРФ-24”.
Москва - 2000
Печатается по постановлению Редакционно-издательского Совета МГУДТ.
Работа рассмотрена на заседании кафедры физики и рекомендована к печати.
Заведующий кафедрой доц. Шапкарин И.П.
Авторы: доц. Разинова С.М.
к.ф-м.н. Родэ С.В.
Методические указания к лабораторной работе по разделу “Оптика”. “Определение показателя преломления жидкости при помощи рефрактометра ИРФ-24”.
г. Москва
Типография МГУДТ. 2000 г.
Методические указания содержат теоретическое введение и описание практической части к лабораторной работе, связанной с изучением явления дисперсии и определением показателя преломления жидкости при помощи рефрактометра.
@ МГУДТ 2000
ЛАБОРАТОРНАЯ РАБОТА № 108
ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ
ПРЕЛОМЛЕНИЯ ВЕЩЕСТВА ЖИДКОСТИ
ПРИ ПОМОЩИ РЕФРАКТОМЕТРА ИРФ-24.
Цель работы: изучение зависимости показателя преломления жидкости от длины волны падающего света.
Приборы и принадлежности: рефрактометр ИРФ-24, ртутная лампа.
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ.
Один из законов преломления света утверждает, что показатель преломления вещества есть величина постоянная. Этот закон использовали для решения практических задач, связанных с построением хода светового луча в различных оптических приборах. При решении этих задач не было необходимости уточнять, имеем мы дело с монохроматическим (одноцветным) лучом, или падающий свет имеет сложный состав и содержит в себе волны разных длин.
Следует отметить, однако, что при прохождении луча белого света через трехгранную призму, он разлагается на составные части, образуя сплошной спектр (рис.1). Значит свет разных длин волн преломляется в одном и том же веществе по разному. Это явление, обусловленное зависимостью показателя преломления вещества от длины световой волны, носит название ДИСПЕРСИЯ СВЕТА, а получившийся в результате двукратного преломления призмой спектр носит название ДИСПЕРСИОННЫЙ СПЕКТР.
Дисперсия света может быть объяснена на основе электромагнитной теории и электронной теории вещества. Для этого нужно рассмотреть процесс взаимодействия электромагнитной волны, проходящей через вещество, с электронами в атоме вещества. Движение электронов в атоме подчиняется законам квантовой механики и рассмотрение этой задачи представляет значительные трудности. Однако, как показал Лоренц, для качественного понимания многих оптических явлений достаточно ограничиться гипотезой о наличии между электронами в атоме квазиупругой связи. Будучи выведенными из положения равновесия, такие электроны начнут колебаться, постепенно теряя энергию колебания на излучение электромагнитных волн. В результате колебания будут затухающими, и затухание можно учесть, введя «силу трения затухания», пропорциональную скорости.
Э

красный оранжевый желтый зеленый голубой синий фиолетовый
Э
Рис.1
При прохождении через вещество электромагнитной волны, электрон в атоме вещества оказывается под воздействием силы Лоренца со стороны электромагнитного поля. Эта сила равна:
![]() ,
(1)
,
(1)
где е - заряд
электрона,
![]() - напряженность электрического поля,
- напряженность электрического поля,
![]() -
скорость электрона в веществе,
-
скорость электрона в веществе,
![]() - индукция магнитного поля,
- индукция магнитного поля,
![]() -
напряженность магнитного поля, связанная
с индукцией соотношением
-
напряженность магнитного поля, связанная
с индукцией соотношением
![]() (если
= 1).
(если
= 1).
Расчет показывает, что сила воздействия на электрон со стороны магнитного поля оказывается в 104 раз меньше силы воздействия электрического поля, поэтому вторым слагаемым в силе Лоренца можно пренебречь и считать, что на электрон действует только сила со стороны электрического поля. Так как эта сила изменяется по гармоническому закону, то она является вынуждающей силой, а колебания электрона - ВЫНУЖДЕННЫМИ КОЛЕБАНИЯМИ.
F=eE=eE0sin (t+0) , (2)
где 0
- начальная фаза колебания электрона,
определяемая его координатами. Е0
- амплитуда напряженности электрического
поля,
- циклическая частота колебаний вектора
![]() в световой волне.
в световой волне.
Кроме вынуждающей силы на электрон в атоме, исходя из наших упрощенных предположений, будет действовать возвращающая КВАЗИУПРУГАЯ СИЛА:
![]()
![]() Fупр=
Fупр=![]() ,
(3)
,
(3)
где х - смещение электрона от положения равновесия, к - коэффициент жесткости, 0 - СОБСТВЕННАЯ циклическая частота колебаний электрона в атоме.
Чтобы упростить вычисления, пренебрегаем затуханием за счет излучения. Тогда под действием этих сил электрон в атоме будет совершать колебательное движение, дифференциальное уравнение которое будет иметь вид:
![]() . (4)
. (4)
Из теории дифференциальных уравнений известно, что решение (4) имеет вид: x = xmaxsin(t+0), где амплитуда
![]() .
(5)
.
(5)
Рассмотрим теперь электронную теорию дисперсии. Для упрощения будем считать молекулы вещества неполярными, т.е. молекулы превращаются в диполи только под действием внешнего электрического поля. Кроме того, поскольку массы ядер велики по сравнению с массой электронов, пренебрежем смещением ядер из положения равновесия под действием световой волны. В этом приближении дипольный электрический момент молекулы можно представить в виде: pi = exi max, где хмах - максимальное смещение i - того электрона из положения равновесия под действием электромагнитной волны. Так как входящие в состав молекулы электроны имеют набор собственных частот колебания 0i , то подставив формулу (5) в выражение для дипольного электрического момента молекулы, получим:
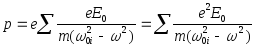 . (6)
. (6)
Обозначим число
молекул в единице объема буквой
N.
Произведение
Np
дает вектор
поляризации
![]() ,
который, как следует из теории диэлектриков,
равен P=Np=0E,
где 0
- электрическая постоянная
вакуума,
-
диэлектрическая восприимчивость,
связанная с диэлектрической проницаемостью
вещества соотношением:
,
который, как следует из теории диэлектриков,
равен P=Np=0E,
где 0
- электрическая постоянная
вакуума,
-
диэлектрическая восприимчивость,
связанная с диэлектрической проницаемостью
вещества соотношением:
=1+,
=![]() .
.
![]() (7)
(7)
Так как показатель
преломления для прозрачных диэлектриков![]() ,
то
,
то
![]() откуда
откуда
![]() .
(8)
.
(8)
Как видно из (8)
показатель преломления вещества является
функцией частоты
падающего света (см. рис.2) и эта зависимость
носит резонансный характер. Другими
словами, при частотах, заметно отличающихся
от всех собственных частот 0i
электронов,
сумма в (8) будет мала по сравнению с
единицей, так что n2
1. Показатель
преломления в этом случае растет с
увеличением частоты падающего света
(![]()
0) и дисперсия
носит название НОРМАЛЬНОЙ ДИСПЕРСИИ.
0) и дисперсия
носит название НОРМАЛЬНОЙ ДИСПЕРСИИ.
Вблизи каждой из собственных частот 0i функция (8) терпит разрыв: при стремлении к 0i слева она обращается в + , при стремлении справа - в - (пунктир на рис.2).
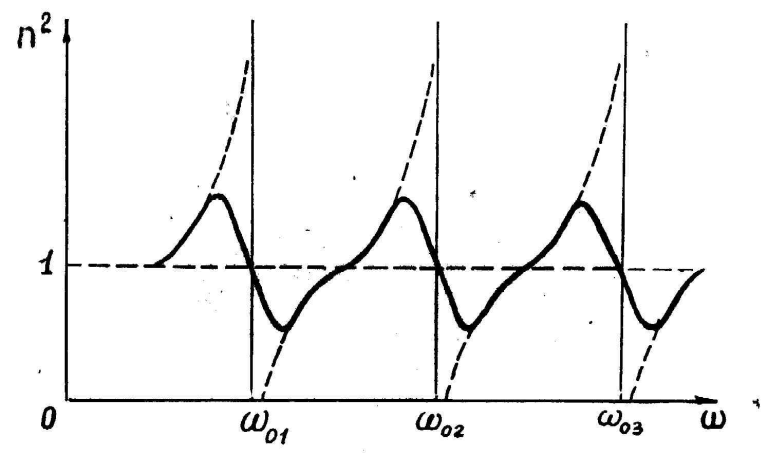
Рис.2
Такое поведение
функции (8) обусловлено тем, что мы
пренебрегли «трением
излучения».
Из теории колебаний следует, что при
отсутствии трения амплитуда вынужденных
колебаний при резонансе обращается в
бесконечность. Учет трения излучения
приводит к зависимости n2
от ,
показанной на рис.2 сплошной кривой. В
области
0i
наблюдается
падение показателя преломления с ростом
частоты (![]()
0). Эта
область называется областью АНОМАЛЬНОЙ
ДИСПЕРСИИ и соответствует резонансному
поглощению света веществом.
0). Эта
область называется областью АНОМАЛЬНОЙ
ДИСПЕРСИИ и соответствует резонансному
поглощению света веществом.
Переходя от n2
к n
и от
к
![]() ,
получим кривую n
= f(),
изображенную на рис.3 (дан лишь участок
кривой в области одной из резонансных
длин волн 0i).
Участки кривой 1 -2 и 3 - 4 соответствуют
области нормальной дисперсии (
,
получим кривую n
= f(),
изображенную на рис.3 (дан лишь участок
кривой в области одной из резонансных
длин волн 0i).
Участки кривой 1 -2 и 3 - 4 соответствуют
области нормальной дисперсии (![]()
0), а участок
2 - 3 - аномальной дисперсии (
0), а участок
2 - 3 - аномальной дисперсии (![]() 0).
0).
Для всех прозрачных бесцветных веществ функция n = f() имеет в видимой части спектра характер, показанный на рис.3 участком кривой 3 - 4.
Как видно из рис.3, с ростом длины волны света, проходящего через вещество, показатель преломления падает. Отсюда следует, что наибольшее преломление в трехгранной призме испытывают фиолетовые лучи, в дисперсионном спектре фиолетовый цвет будет располагаться ближе к основанию призмы.
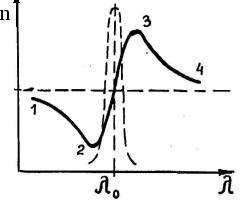
Рис.3.
ОПИСАНИЕ УСТАНОВКИ И МЕТОДА ИЗМЕРЕНИЙ.
Рефрактометр, применяемый в данной работе, служит для определения показателя преломления жидких и твердых прозрачных сред. Метод основан (см. рис.4) на измерении углов отклонения лучей, прошедших через прямоугольную призму при условии, что на верхнюю грань призмы падает почти скользящий пучок света. На горизонтальную грань призмы помещают прозрачный цилиндрический сосуд с исследуемой жидкостью.
Если луч, падающий из среды с показателем преломления n1 (в данном случае такой средой является исследуемая жидкость), направить так, чтобы угол был близок к 90О, то во второй среде с большим показателем преломления n2 (т.е. в призме) он пойдет под углом . По законам преломления для этой границы раздела углы и связаны соотношением:
![]() .
(9)
.
(9)
Если угол близок к 90О, то формула (9) приобретает вид:
![]() .
(10)
.
(10)
Выходя из призмы в воздух, луч еще раз преломляется, образуя угол и на границе раздела между вертикальной гранью призмы и воздухом. Углы и связаны по законам преломления для данной границы раздела соотношением:
![]() ,
(11)
,
(11)
где единица представляет собой абсолютный показатель преломления воздуха, а угол связан с углом равенством:
![]() .
(12)
.
(12)
n1
S’
S
I
‘
‘
II

Рис. 4
С учетом (12) равенство (11) можно переписать:
![]() .
(13)
.
(13)
Выражая из (10) значение sin, а из (13) - cos, возводя их в квадрат и складывая левые и правые части этих равенств, получим формулу для определения показателя преломления n1, исследуемой жидкости через известный показатель преломления призмы n2 и измеряемый угол :
![]() .
(14)
.
(14)
Если луч S’, изображенный на рис. 1 пунктирной линией, падает на призму под углом значительно меньшим 90О, то из формулы (10) следует, что и соответствующий ему угол станет также меньше, чем этот же угол для почти скользящего луча S. С уменьшением угла увеличивается разность (/2 - ), а, следовательно, и угол (ф-ла (13)), т.е. угол становится минимальным только в том случае, если угол близок к 90О. Этот минимальный угол , соответствующий почти скользящему лучу S, измеряется с помощью рефрактометра.
Рис. 5 поясняет принципиальную схему устройства рефрактометра (вид сверху). Основными частями прибора являются эталонная призма (4) из тяжелого флинта (сорт стекла), показатель преломления которой известен с большой точностью; сосуд с исследуемой жидкостью, помещенный на горизонтальную грань призмы; осветительная система (1), (2), (3); зрительная труба (7) с приспособлением для определения нулевого положения установки; отсчетное устройство (13) (спиральный микрометр).
1 2 3 4 5 6 7
a
b P’ b’

13
8
11 12
P
10
9
a’
Рис. 5.
Осветительная система состоит из источника света (1), дающего линейчатый спектр, и конденсора (2), создающего параллельный пучок лучей. Конденсор снабжен зубчатой диафрагмой (3) для срезания лучей S’, идущих выше лучей S, изображенных на рис. 4.
Зрительная труба (7), с помощью которой наблюдают преломленные лучи, состоит из объектива (6), входной диафрагмы (5), перекрестья (8), нанесенного на прозрачную стеклянную пластинку, окуляра (9) и призм полного внутреннего отражения Р и Р’. Труба может поворачиваться относительно горизонтальной оси, т.е. занимать положение, соответствующее положениям I и II на рис 4.
В идеально изготовленном рефрактометре ось зрительной трубы в положении I (рис.4) должна быть перпендикулярна вертикальной грани призмы. При этом отсчет по спиральному микрометру должен быть равен нулю. На практике при указанном положении зрительной трубы шкала отсчетного устройства показывает некоторый угол 0, называемый нулевой точкой призмы. При измерении угла эту нулевую точку 0 нужно вычитать из показания шкалы.
Нулевую точку призмы измеряют следующим образом. Центр перекрестья (8) совпадает с оптической осью трубы аа’. Между окуляром (9) и перекрестьем (8) помещена призма Р полного внутреннего отражения, закрывающая только левую часть перекрестья. При этом в поле зрения окуляра (9) видна картина, представленная на рис. 6а.
Для снятия нулевого отсчета открывают заслонку (12), и свет от источника (11) при определенном положении зрительной трубы попадает в маленькое окошко (10), расположенное на левой стороне зрительной трубы. Лучи, идущие от источника (11), через окошко (10) попадают на призму Р полного внутреннего отражения, которая отбрасывает эти лучи на перекрестье (8), освещая только левую его половину. Призма Р поворачивает эти лучи на 90О и направляет на вертикальную грань эталонной призмы (4). Т.к. эталонная призма находится в фокусе объектива (6), то лучи, отраженные от ее поверхности, идут обратно вдоль зрительной трубы и дают изображение левой половины перекрестья в правой части поля зрения окуляра (9). При этом, если нормаль bb’ к отражающей грани призмы (4) одновременно перпендикулярна к оптической оси aa’ зрительной трубы, то изображение перекрестья в правой половине поля зрения окуляра должно быть либо совмещено с нитями самого перекрестья, либо симметрично относительно них (рис. 6б) Отсчет 0, соответствующий рис.6б, является нулевой точкой призмы.
Угол соответствует на рис.4 положению II зрительной трубы. При этом, если угол наименьший (т.е. угол 90О), то изображение верхней границы спектральной линии должно совпасть с перекрестьем (рис. 7), а поле зрения трубы должно состоять из двух половин разной интенсивности: нижняя часть поля зрения будет освещена, а верхняя - останется темной. Граница раздела света и тени, совпадающая с перекрестьем, определяется лучом S, выходящим из призмы под наименьшим углом (рис.4).

а б
Рис. 6.

Рис. 7.
Отсчетное устройство (13), служащее для измерения углов поворота зрительной трубы, представляет собой микроскоп со спиральным микрометром. В поле зрения микроскопа одновременно видны два-три штриха лимба, пронумерованные на рис.8 цифрами 11, 12, 13, обозначающие целые градусы измеряемого угла; неподвижная шкала (красная) десятых долей градуса с делениями от “0” до “10”; круговая шкала для отсчета сотых и тысячных долей градуса, обозначенная на рис.8 цифрами 65, 70, 75, 80 и десять двойных витков спирали. Чтобы произвести отсчет, необходимо маховиком, находящимся под микроскопом, подвести двойной виток спирали так, чтобы градусный штрих, расположенный в зоне двойных витков, оказался точно посредине между линиями двойного витка спирали.
Отсчет, снятый по лимбу микроскопа для случая, показанного на рис. 5, равен 12 градусам (градусное деление, попавшее в область двойных спиральных витков), 2 десятых доли градуса (снятые по вертикальной шкале), 72 тысячные доли градуса (снятые по круговой шкале). Десятитысячные доли градуса определяют на глаз. Окончательный отсчет = 12,2725О. Для дальнейших расчетов это значение угла, выраженное в десятичных долях градуса необходимо перевести в минуты и секунды.
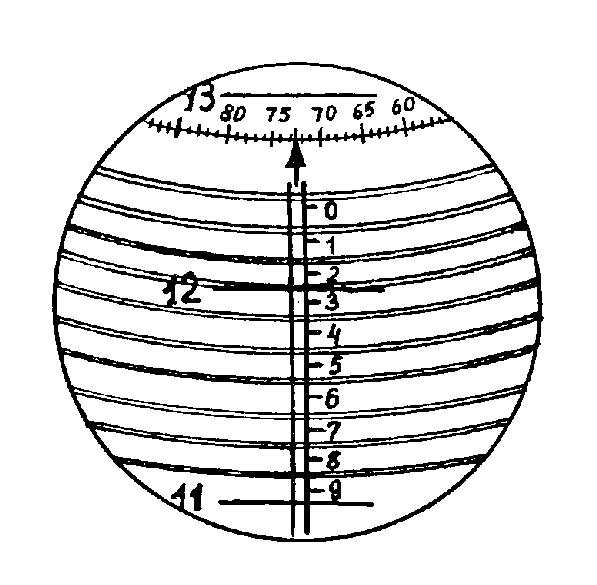
Рис. 8.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.
Задание 1. Определение нулевого положения зрительной трубы.
1.Закройте источник света (1) зубчатой диафрагмой (3) на конденсоре так, чтобы свет не попадал в зрительную трубу.
2.Откройте верхнюю часть диафрагмы (5) зрительной трубы (7), повернув ее до конца от себя.
3.Откройте диафрагму (12) осветительной лампы (11) так, чтобы свет от нее попал через боковое окошко (10) в зрительную трубу.
4.Установите трубу в горизонтальное положение так, чтобы произошло совмещение перекрестья (как показано на рис.7б). При этом грубую наводку производят при освобожденном стопорном винте, а точную наводку - при зажатом стопорном винте микровинтом.
5.Снимите нулевое показание 0 по отсчетной шкале микроскопа (13). Произведите эти измерения не менее трех раз. Все полученные значения 0 запишите в таблицу 1 и найдите среднее значение нулевого отсчета. Это значение также занесите в таблицу.
Задание 2. Определение показателя преломления жидкости.
1.Закройте диафрагмой (12) осветительную лампочку (11).
2.Поднимите до половины диафрагму на выходном конденсоре (2), чтобы лучи от источника попадали в зрительную трубу.
3.Опустите входную диафрагму (3) зрительной трубы вниз, повернув ее на себя.
4.Отпустите стопорный винт и, поворачивая зрительную трубу вниз, найдите преломленный луч. Микрометрическим винтом подведите перекрестье к верхней границе полосы (сначала желтой, затем зеленой и фиолетовой).
5.Снимите показания на отсчетной шкале микроскопа и занесите их в таблицу 1 (i’= ж’, з’, ф’).
6.Вычислите значения углов i для трех полос:
ж = ж’ - 0ср ; з = з’ - 0 ср; ф = ф’ - 0 ср .
Таблица 1
|
Цвет линии ртутного спектра |
Длина волны ( |
Показатель преломления призмы n2 |
0 |
0ср |
i’ |
i = i’ - 0ср |
n1 по ф-ле (14)
|
|
желтый |
5791 |
1,619 |
|
|
|
|
|
|
зеленый |
5458 |
1,621 |
|
|
|
|
|
|
фиолетовый |
4358 |
1,639 |
|
|
|
|
|
7.Определите показатель преломления жидкости по формуле (14), используя известные значения n2 для данных линий спектра. Вычисления производить до тысячных долей числа. Результаты вычислений запишите в таблицу 1 и объясните, как полученные значения показателей преломления подтверждают сущность явления дисперсии
Вопросы для допуска к работе.
1.В чем заключается явление дисперсии?
2.Как снять нулевой отсчет по шкале рефрактометра?
3.Как наблюдать дисперсию?
4.Для чего служит прибор рефрактометр?
5.Причина преломления света на границе раздела прозрачных сред.
Вопросы для защиты работы.
1.Вывод расчетной формулы для определения показателя преломления вещества.
2.Абсолютный и относительный показатель преломления вещества и связь их со скоростью света.
3.Электронная теория дисперсии.
4.Ход лучей в рефрактометре.
5.Анализ полученных результатов.
