
ЛАБОРАТОРНАЯ РАБОТА № 110 ИЗУЧЕНИЕ ЛИНЕЙЧАТЫХ СПЕКТРОВ
..doc
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ДИЗАЙНА и ТЕХНОЛОГИИ
Методические указания к лабораторной работе №110
“Изучение линейчатых спектров”.
Москва - 2000
Печатается по постановлению Редакционно-издательского Совета МГУДТ.
Работа рассмотрена на заседании кафедры физики и рекомендована к печати.
Заведующий кафедрой доц. Шапкарин И.П.
Автор: к.ф-м.н. Родэ С.В.
Методические указания к лабораторной работе по разделу “Оптика”. “Изучение линейчатых спектров”.
г. Москва
Типография МГУДТ. 2000 г.
Методические указания содержат теоретическое введение и описание практической части к лабораторной работе, связанной с изучением и методами измерения показателя преломления вещества.
@ МГУДТ 2000
ЛАБОРАТОРНАЯ РАБОТА № 110
ИЗУЧЕНИЕ ЛИНЕЙЧАТЫХ СПЕКТРОВ.
Цель работы: проверка сериальных закономерностей в спектре атома водорода.
Приборы и принадлежности: монохроматор УМ-2, ртутная лампа, водородная газоразрядная трубка.
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ.
Известно,
что в процессе интерференции, дифракции
и дисперсии белый свет разлагается на
составляющие его цвета, соответствующие
приблизительно интервалам длин волн
от 7500![]() до 4000
до 4000
![]() .
Оптический диапазон электромагнитных
волн включает в себя не только видимый
свет, но и волны длина которых больше
7500
.
Оптический диапазон электромагнитных
волн включает в себя не только видимый
свет, но и волны длина которых больше
7500![]() (ИНФРАКРАСНАЯ
область спектра), а также волны, длина
которых меньше 4000
(ИНФРАКРАСНАЯ
область спектра), а также волны, длина
которых меньше 4000![]() (УЛЬТРАФИАЛЕТОВАЯ
область спектра).
(УЛЬТРАФИАЛЕТОВАЯ
область спектра).
Скорость света и длины волны зависят от природы среды, в которой свет распространяется; частота колебаний электромагнитного поля волны от природы волны не зависит.
Отдел физики, изучающий получение и происхождение разного рода спектров, называется СПЕКТРОСКОПИЕЙ. Приборы, позволяющие получить и изучить спектры, называются СПЕКТРАЛЬНЫМИ ПРИБОРАМИ. Простейшим типов таких приборов является СПЕКТРОСКОП, позволяющий наблюдать спектры визуально, т.е. непосредственно зрением. Если спектроскоп снабжен приспособлением, позволяющим измерять, длинны длины волн наблюдаемого спектра, он называется спектроскопом. Если спектроскоп снабжен приспособлением, допускающим фиксацию спектра фотопластинкой, или каким-либо светочувствительным элементом: фотоэлементом, термоэлементом и т.д., то он называется СПЕКТРОГРАФОМ.
1.Виды спектров и процессы излучения.
СПЛОШНЫМИ СПЕКТРАМИ называют спектры, между участками которых нельзя указать отчетливых границ. ЛИНЕЙЧАТЫМИ СПЕКТРАМИ называют спектры, разделенные на узкие линии с достаточно резкими очерченными границами. Такие линии группируются в спектральные серии, характер распределения линий, в которых может быть различным. ПОЛОСАТЫМИ СПЕКТРАМИ называются спектры, которые при малой дисперсии спектрального прибора представляются в виде ряда полос.
Различают СПЕКТРЫ ИСПУСКАНИЯ и СПЕКТРЫ ПОГЛАЩЕНИЯ. Спектры испускания, как показывает их название, получаются при спектральном разложении излучения, исходящего от каких-либо источников излучения. Иногда эти спектры называют ЭМИССИОННЫМИ. Спектры поглощения, наблюдаются в виде темных участков, состоящих из линий или полос, проявляющихся на фоне сплошного спектра, когда излучение, идущее от источников сплошного спектра, прежде чем поступить в спектральный прибор, проходит через какую - либо поглощающую среду.
Все источники излучения могут быть разделены на два основных вида: на источники “температурного излучения”, например, светящаяся нить лампы накаливания, и на источники “нетемпературного излучения”, которые иногда называют источниками “холодного света”.
Примером ХОЛОДНЫХ ИСТОЧНИКОВ ИЗЛУЧЕНИЯ являются ГАЗОРАЗРЯДНЫЕ ТРУБКИ низкого давления, наполненные одноатомными ( гелий, неон, и т.д.) или многоатомным (азот, окись углерода, двуокись углерода) газом. Излучение холодных источников называется ХАРАКТЕРИСТИЧЕСКИМ, т.к. изучение спектра этого излучения позволяет определить природу газа, испускающего данное излучение. При этом излучение одноатомного газа даёт линейчатые спектры, а изучение многоатомного - полосатые спектры.
Для уяснения природы процессов, приводящих к тому, что атомы или молекулы, наполняющие газоразрядные трубки, начинают испускать изучение, следует обратиться к теории КВАНТОВ, предложенной Планком в 1889 г. и составившей основу всей современной квантовой физики. Согласно этой теории атом или молекула может поглотить или излучить энергию только отдельными порциями, т.е. квантами, величина которых определяется равенством:
![]() ,
(1)
,
(1)
где e- поглощаемая или испускаемая порция энергии; n,l- частота или длинна волны поглощаемого или испускаемого излучения; с - скорость света и h- некоторая универсальная константа, получившая название ПОСТОЯННАЯ ПЛАНКА. В 1905 г. Эйнштейн дополнил эту теорию, предположив, что и само излучаемое электромагнитное поле, несмотря на свою волновую природу, состоит из особого рода частиц, которые могут быть названы “световыми квантами” или ФОТОНАМИ.
Значение теории квантов в учении о спектрах легко уяснить, рассматривая ЭЛЕМЕНТАРНЫЕ КВНТОВЫЕ ПРРОЦЕССЫ, которые имеют место в газоразрядных источниках света.
Так,
в газоразрядных трубках
низкого давления, напряженность
электрического поля в которых велика,
более быстрыми частицами являются
электроны. Однако, среди электронов, в
свою очередь, следует различать массу
сравнительно медленных электронов,
которые можно обозначить значком
![]() ,
и
малую
часть быстрых электронов, которые можно
обозначить значком
,
и
малую
часть быстрых электронов, которые можно
обозначить значком
![]() .
Тогда процесс столкновения быстрого
электрона
.
Тогда процесс столкновения быстрого
электрона
![]() с какой-либо частицей К
(атомом или молекулой) можно представить
такой схемой:
с какой-либо частицей К
(атомом или молекулой) можно представить
такой схемой:
![]() Схема
А
Схема
А
При
этом предполагается, что разница между
энергией быстрого электрона
![]() и медленного электрона
и медленного электрона
![]() переходит к частице К,
которая при этом переходит в особое
состояние, называемое ВОЗБУЖДЕННЫМ
СОСТАЯНИЕМ.
Такая возбужденная частица обозначена
в схеме А значком
переходит к частице К,
которая при этом переходит в особое
состояние, называемое ВОЗБУЖДЕННЫМ
СОСТАЯНИЕМ.
Такая возбужденная частица обозначена
в схеме А значком
![]() ,
а процесс, изображенный на схеме А
называется ПРЦЕССОМ
УДАРНОГО ВОЗБУЖДЕНИЯ.
Однако, частица
,
а процесс, изображенный на схеме А
называется ПРЦЕССОМ
УДАРНОГО ВОЗБУЖДЕНИЯ.
Однако, частица
![]() оказывается неустойчивой. Благодаря
этому, спустя малое время (порядка 10-3
сек), которое называется ВРЕМЕНЕМ
ЖИЗНИ ВОЗБУЖДЕННОГО СОСТАЯНИЯ,
частица К¢¢
испускает полученную энергию в виде
светового кванта, энергия которого
определяется формулой (1). Такой процесс
может быть представлен так:
оказывается неустойчивой. Благодаря
этому, спустя малое время (порядка 10-3
сек), которое называется ВРЕМЕНЕМ
ЖИЗНИ ВОЗБУЖДЕННОГО СОСТАЯНИЯ,
частица К¢¢
испускает полученную энергию в виде
светового кванта, энергия которого
определяется формулой (1). Такой процесс
может быть представлен так:
![]() ,
Схема
Б
,
Схема
Б
где
hv
условно
обозначен световой квант или фотон.
Процесс, изображенный на схеме Б,
называется ПРОЦЕССОМ
СПОНТАНННОГО (самопроизвольного)
ИЗЛУЧЕНИЯ или ПРОЦЕССОМ ЛЮМИНИСЦЕНЦИИ.
Возможны случаи, когда возбужденная
частица
![]() ,
не успевшая еще испустить фотон,
испытывает столкновение со сравнительно
медленной частицей К.
В этом случае энергия возбуждения e
= hn,
теряемая частицей
,
не успевшая еще испустить фотон,
испытывает столкновение со сравнительно
медленной частицей К.
В этом случае энергия возбуждения e
= hn,
теряемая частицей
![]() ,
переходит в кинетическую энергию
столкнувшихся частиц, которые после
столкновения разлетаются с повышенной
скоростью. Такой процесс называется
процессом ТУШЕНИЯ
ЛЮМИНИСЦЕНЦИИ:
,
переходит в кинетическую энергию
столкнувшихся частиц, которые после
столкновения разлетаются с повышенной
скоростью. Такой процесс называется
процессом ТУШЕНИЯ
ЛЮМИНИСЦЕНЦИИ:
![]() ,
Cхема
В
,
Cхема
В
где
К
– частицы, преобретшие повышенную
скорость. Процесс тушения люминесценции,
протекающей по схеме В, сопровождается
увеличением числа частиц, несущих
повышенную кинетическую энергию, что
равносильно росту температуры газа.
Легко видеть, что при низких давлениях
газа в газоразрядной трубке возбужденные
частицы
![]() теряют свою энергию в основном в
результате процесса люминесценции,
изображенной схемой Б. В этом случае
газ практически не нагревается. Именно
поэтому газоразрядные трубки низкого
давления, излучающие кванты света -
фотоны, и называются “источники
холодного излучения”.
С ростом давления в газоразрядной трубке
преобладает процесс В, в результате
чего газ сильно нагревается. В этом
случае спектр излучения трубки утрачивает
свою ”характеристичность”,
приближаясь к сплошному спектру
температурных источников излучения.
теряют свою энергию в основном в
результате процесса люминесценции,
изображенной схемой Б. В этом случае
газ практически не нагревается. Именно
поэтому газоразрядные трубки низкого
давления, излучающие кванты света -
фотоны, и называются “источники
холодного излучения”.
С ростом давления в газоразрядной трубке
преобладает процесс В, в результате
чего газ сильно нагревается. В этом
случае спектр излучения трубки утрачивает
свою ”характеристичность”,
приближаясь к сплошному спектру
температурных источников излучения.
-
Теория спектров водородоподобных атомов Н. Бора.
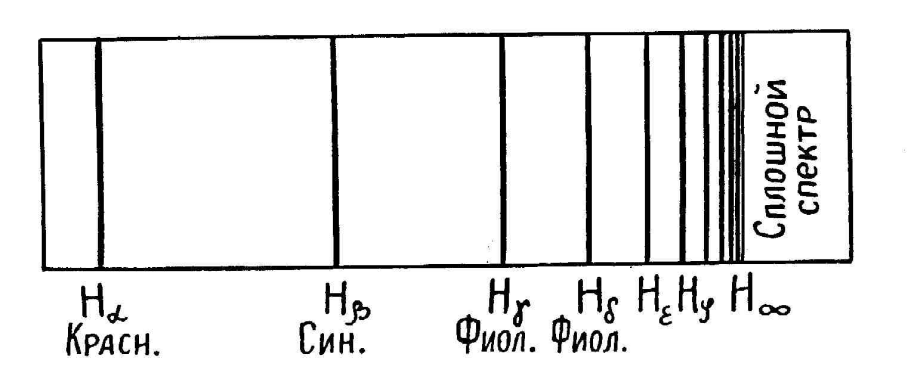
Если
излучение, испускаемое разрядной
трубкой, наполненной молекулярным
водородом, исследовать при помощи
спектрального прибора, то в видимой
части спектра отчетливо видны четыре
спектральные линии, которые обычно
обозначаются буквой Н
с соответствующими индексами
-
красная
![]() линия, сине-зелёная
линия, сине-зелёная
![]() линия, фиолетовая
линия, фиолетовая
![]() линия и фиолетовая
линия и фиолетовая
![]() линия. На рис.1 показан спектр, полученный
при помощи спектрального прибора,
обладающего независимой от длинны волны
дисперсией. Этот спектр включает не
только указанные видимые линии, но и
ближайшие к ним линии со стороны более
коротких ультрафиолетовых волн - линии
He,
Hj
и т.д. - вплоть до “граничной
линии”
H¥,
за которой следует область сплошного
спектра.
линия. На рис.1 показан спектр, полученный
при помощи спектрального прибора,
обладающего независимой от длинны волны
дисперсией. Этот спектр включает не
только указанные видимые линии, но и
ближайшие к ним линии со стороны более
коротких ультрафиолетовых волн - линии
He,
Hj
и т.д. - вплоть до “граничной
линии”
H¥,
за которой следует область сплошного
спектра.
Рис.1
Все линии обязаны своим происхождением излучению возбужденных атомов водорода, образующихся в разряде в результате диссоциации на атомы молекул водорода, возбуждаемых ударами быстрых электронов.
В
расположении указанных линий легко
заметить следующую закономерность.
Видно, что расстояние между линиями
![]() и
и
![]() сравнительно велико, расстояние между
линиями
сравнительно велико, расстояние между
линиями
![]() и
и
![]() уже меньше, а расстояние между линиями
уже меньше, а расстояние между линиями
![]() и
и
![]() еще меньше и т.д., так что расстояния
между смежными линиями стремятся к
нулю, что создает впечатление о непрерывном
переходе линейчатого спектра в сплошной
спектр. Такая закономерность позволяет
думать, что в её основе лежит какой-то
особый закон,
во
всяком случае, можно сразу сказать, что
совокупность подобных линий образует
некоторую СПЕКТРАЛЬНУЮ
СЕРИЮ.
А так как рассматриваемая серия была
подробно изучена Бальмером,
то она называется СЕРИЕЙ
БАЛЬМЕРА.
еще меньше и т.д., так что расстояния
между смежными линиями стремятся к
нулю, что создает впечатление о непрерывном
переходе линейчатого спектра в сплошной
спектр. Такая закономерность позволяет
думать, что в её основе лежит какой-то
особый закон,
во
всяком случае, можно сразу сказать, что
совокупность подобных линий образует
некоторую СПЕКТРАЛЬНУЮ
СЕРИЮ.
А так как рассматриваемая серия была
подробно изучена Бальмером,
то она называется СЕРИЕЙ
БАЛЬМЕРА.
В 1885 г. БАЛЬМЕР предложил формулу, которая позволяет вычислять длины волн отдельных линий изученной им серии. Эта ФОРМУЛА БАЛЬМЕРА имеет следующий вид:
![]() ,
(2)
,
(2)
где
n-
числа 3,4,5... , а
![]() - соответствующие этим числам длинны
волн линий
- соответствующие этим числам длинны
волн линий
![]() и т.д., причем, значению
и т.д., причем, значению
![]() соответствует линия
соответствует линия
![]() ,
длинна волны которой
,
длинна волны которой
![]() .
Проверка этой формулы может быть
произведена путем расчета величины
.
Проверка этой формулы может быть
произведена путем расчета величины
![]() ,
которая должна получатся одинаковой
при любой подстановке в (2) какого-либо
числа n>>3
и соответствующего ему значения
,
которая должна получатся одинаковой
при любой подстановке в (2) какого-либо
числа n>>3
и соответствующего ему значения
![]() .
Для вакуума
.
Для вакуума
![]() .
.
Выяснение
физической сущности закономерности,
выражаемой формулой Бальмера (2) положило
начало развитию науки о строении атомов
и молекул методами спектроскопии. Весьма
интересно, что толчком к этому исследованию
явилось чисто алгебраическое преобразование
формулы (2), которое было выполнено
Ридбергом. Он учел, что в спектроскопии
весьма часто вместо величин длин волн
l
используют обратные им величины
![]() ,
которые называют ВОЛНОВЫМИ
ЧИСЛАМИ
и которые мы будем обозначать знаком
,
которые называют ВОЛНОВЫМИ
ЧИСЛАМИ
и которые мы будем обозначать знаком
![]() ,
чтобы не путать их с частотой
,
чтобы не путать их с частотой
![]() колебаний электромагнитного поля в
световых волнах. Связь величин
колебаний электромагнитного поля в
световых волнах. Связь величин
![]() выражается очевидными соотношениями:
выражается очевидными соотношениями:
![]() .
(3)
.
(3)
С учетом соотношений формулу (2) Ридберг переписал так:
![]() .
(4)
.
(4)
Вводя обозначение:
![]() ,
(5)
,
(5)
формулу (4) можно представить в виде:
![]() .
(6)
.
(6)
В последующем величина RH получила название КОНСТАНТЫ РИДБЕРГА ДЛЯ СПЕКТРОВ АТОМОВ ВОДОРОДА. Для краткости формулу (6) мы будем называть ФОРМУЛОЙ БАЛЬМЕРА - РИДБЕРГА.
Так
как между волновыми числами
![]() и частотами колебаний существует прямая
пропорциональность, вид формулы (6)
наводит на мысль, что излучаемые атомами
кванты света связанны с переходами
излучающих электронов внутри атома
водорода между какими-то двумя различными
или, как говорят, “дискретными”
состояниями. Это соображение было
принято во внимание Н.
Бором
в его объяснении физического смысла
рассматриваемой формулы.
В
основу своих рассуждений Бор положил
гипотезу Резерфорда,
согласно которой
атомы
элементов представляют собой планетарные
системы, состоящие из центрального
положительно заряженного ядра и
электронов, вращающихся вокруг ядра по
замкнутым орбитам.
Простейшими из такого рода систем
являются ВОДОРОДОПОДОБНЫЕ
АТОМЫ,
состоящие из ядра, несущего Z
положительных элементарных зарядов
электричества, и единственного
отрицательного электрона, вращающегося
по круговой орбите вокруг ядра. Атом
водорода является первым примером
такого рода атомов, так как его ядро
является элементарной частицей,
называемой “протоном”,
для которого Z
=
1.
К числу водородоподобных атомов относится
также ион гелия
и частотами колебаний существует прямая
пропорциональность, вид формулы (6)
наводит на мысль, что излучаемые атомами
кванты света связанны с переходами
излучающих электронов внутри атома
водорода между какими-то двумя различными
или, как говорят, “дискретными”
состояниями. Это соображение было
принято во внимание Н.
Бором
в его объяснении физического смысла
рассматриваемой формулы.
В
основу своих рассуждений Бор положил
гипотезу Резерфорда,
согласно которой
атомы
элементов представляют собой планетарные
системы, состоящие из центрального
положительно заряженного ядра и
электронов, вращающихся вокруг ядра по
замкнутым орбитам.
Простейшими из такого рода систем
являются ВОДОРОДОПОДОБНЫЕ
АТОМЫ,
состоящие из ядра, несущего Z
положительных элементарных зарядов
электричества, и единственного
отрицательного электрона, вращающегося
по круговой орбите вокруг ядра. Атом
водорода является первым примером
такого рода атомов, так как его ядро
является элементарной частицей,
называемой “протоном”,
для которого Z
=
1.
К числу водородоподобных атомов относится
также ион гелия
![]() ,
для которого Z
= 2,
а также - дважды ионизированного атома
лития
,
для которого Z
= 2,
а также - дважды ионизированного атома
лития
![]() ,
для
которого Z
=
3
и т.д.
,
для
которого Z
=
3
и т.д.
Приступая к своему теоретическому исследованию, Бор допустил, что в силу квантовой природы излучения внутри атома проявляются какие-то особенные ограничения, препятствующие такому излучению. При этом он сформулировал следующие положения, которые теперь называются ПОСТУЛАТАМИ БОРА.
ПЕРВЫЙ ПОСТУЛАТ утверждает, что электроны в атомах вращаются по стационарным круговым орбитам, не поглощая и не излучая при этом энергии.
ВТОРОЙ ПОСТУЛАТ утверждает, что поглощение энергии атома сопровождается перескоком электрона с орбиты меньшего радиуса на орбиту большего радиуса, а излучение энергии - наоборот - сопровождается перескоком электрона с орбиты большего радиуса на орбиту меньшего радиуса.
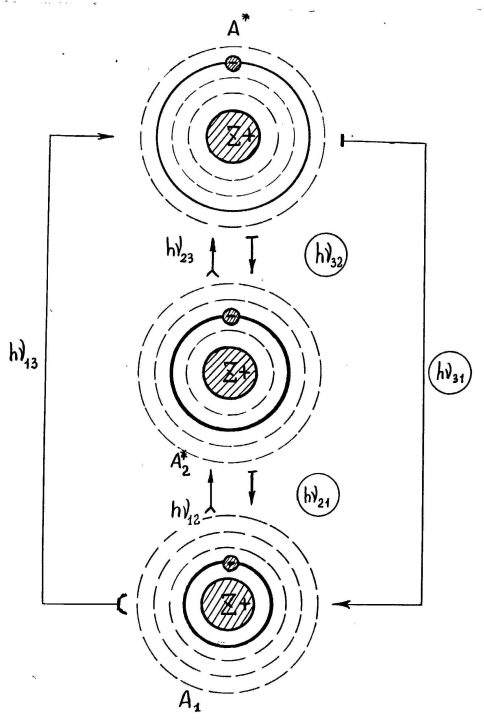
На
рис.2 показаны схемы, наглядно поясняющие
содержание приведенных постулатов
применительно к случаю водородоподобного
атома. Здесь ядро атома показано
затемненным кружочком со знаком
![]() ,
а электрон атома - затемненным знаком
Q.
Стационарные орбиты, по которым в
нормальном атоме А1
или в возбужденных атомах А2*,
А3*
движется
электрон, показаны сплошными круговыми
линиями, при этом условно показаны лишь
3 орбиты и номера орбит обозначены
числами m,
где
m
< n.
Оперенные стрелки показывают возможные
процессы поглощения квантов
,
а электрон атома - затемненным знаком
Q.
Стационарные орбиты, по которым в
нормальном атоме А1
или в возбужденных атомах А2*,
А3*
движется
электрон, показаны сплошными круговыми
линиями, при этом условно показаны лишь
3 орбиты и номера орбит обозначены
числами m,
где
m
< n.
Оперенные стрелки показывают возможные
процессы поглощения квантов
![]() ;
простые стрелки изображают процессы
спонтанного излучения фотонов
;
простые стрелки изображают процессы
спонтанного излучения фотонов
![]() .
При этом энергия, которой соответствует
квантовое число n,
обозначается через
.
При этом энергия, которой соответствует
квантовое число n,
обозначается через
![]() ,
а энергия, которой со
,
а энергия, которой со
ответствует
квантовое число m,
обозначается через
![]() .
.
Рис.2
Тогда
процесс ударного возбуждения протекает
по схеме А, и его можно представить как
перенос электрона с орбиты m
на орбиту n,
чему соответствует изменение энергии
![]() .
Процессу спонтанного излучения,
протекающему по схеме В, будет
соответствовать изменение энергии
.
Процессу спонтанного излучения,
протекающему по схеме В, будет
соответствовать изменение энергии
![]() .
Далее, волновое число
.
Далее, волновое число
![]() ,
соответствующее частоте
,
соответствующее частоте
![]() и длине волны
и длине волны
![]() ,
с учетом (3) выражается формулой :
,
с учетом (3) выражается формулой :
![]() . (7)
. (7)
Отсюда
следует, что для
расчета
значения
![]() необходимо
вычислить значения энергий
необходимо
вычислить значения энергий
![]() атома в двух его состояниях квантового
возбуждения n,
m.
В этом расчете сначала используются
законы классической физики. Так, прежде
всего, заметим что электрон, вращающийся
вокруг ядра, согласно закону Кулона
притягивается к ядру с силой, которая
в системе СИ может быть представлена
равенством:
атома в двух его состояниях квантового
возбуждения n,
m.
В этом расчете сначала используются
законы классической физики. Так, прежде
всего, заметим что электрон, вращающийся
вокруг ядра, согласно закону Кулона
притягивается к ядру с силой, которая
в системе СИ может быть представлена
равенством:
![]() ,
(8)
,
(8)
где
![]() - электрическая постоянная системы СИ;
- электрическая постоянная системы СИ;
![]() - заряд электрона;
- заряд электрона;
![]() - заряд ядра и r-
радиус рассматриваемой орбиты. Эта сила
является центростремительной, и поэтому
может быть представлена в таком виде:
- заряд ядра и r-
радиус рассматриваемой орбиты. Эта сила
является центростремительной, и поэтому
может быть представлена в таком виде:
![]() ,
(9)
,
(9)
где
![]() - масса электрона , v-
скорость его движения по орбите.
- масса электрона , v-
скорость его движения по орбите.
Из сопоставления равенства (8) и равенства (9) получается
![]() .
(10)
.
(10)
Тогда
кинетическую энергию
![]() электрона на рассматриваемой орбите
можно представить так:
электрона на рассматриваемой орбите
можно представить так:
![]() .
(11)
.
(11)
С
другой стороны потенциальная энергия
![]() взаимодействующих зарядов
взаимодействующих зарядов
![]() и
и
![]() равна:
равна:
![]() (12)
(12)
Отсюда видно, что общая энергия Е электрона на орбите радиуса r выражается так:
![]() .
(13)
.
(13)
Согласно
приведенному выше первому постулату,
стационарными будут те орбиты, для
которых радиус
![]() ,
где n-
главное квантовое число орбиты. Энергия
электронов на такой орбите будет:
,
где n-
главное квантовое число орбиты. Энергия
электронов на такой орбите будет:
![]() (14)
(14)
Для
определения величины
![]() Бор предложил ТРЕТИЙ
ПОСТУЛАТ,
сущность которого может быть пояснена
следующим образом. Как известно, для
характеристики вращательного движения
в механике вводится вектор МОМЕНТА
ИМПУЛЬСА
Бор предложил ТРЕТИЙ
ПОСТУЛАТ,
сущность которого может быть пояснена
следующим образом. Как известно, для
характеристики вращательного движения
в механике вводится вектор МОМЕНТА
ИМПУЛЬСА
![]() ,
который в случае отсутствия внешних
сил считается направленным по нормали
к плоскости вращения. Его модуль
определяется равенством:
,
который в случае отсутствия внешних
сил считается направленным по нормали
к плоскости вращения. Его модуль
определяется равенством:
![]() (15)
(15)
Здесь
r-
модуль
радиус-вектора
![]() ,
проведенного из начала координат до
местоположения материальной точки
массой m:
V-модуль
вектора
,
проведенного из начала координат до
местоположения материальной точки
массой m:
V-модуль
вектора
![]() скорости этой точки;
a-
угол между векторами
скорости этой точки;
a-
угол между векторами
![]() и
и
![]() .
Тогда, для случая движения электрона
по круговой орбите радиуса
.
Тогда, для случая движения электрона
по круговой орбите радиуса
![]() со скоростью
со скоростью
![]() выражение (15) записывается так:
выражение (15) записывается так:
![]() ,
(16)
,
(16)
так
как в данном случае
![]() и
и
![]() ,
,
При
этом ТРЕТИЙ
ПОСТУЛАТ БОРА
утверждает, что модуль
![]() вектора
вектора
![]() момента импульса электрона, движущегося
по круговой орбите вокруг ядра, должен
быть пропорционален главному квантовому
числу
n орбиты,
причем коэффициент пропорциональности
должен быть равен
момента импульса электрона, движущегося
по круговой орбите вокруг ядра, должен
быть пропорционален главному квантовому
числу
n орбиты,
причем коэффициент пропорциональности
должен быть равен
![]() .
Другими словами, должно соблюдаться
условие:
.
Другими словами, должно соблюдаться
условие:
![]() .
(17)
.
(17)
Это
равенство дает искомое дополнительное
квантовое условие для определения
величины
![]() .
В самом деле, если возвести обе части
равенства (17) в квадрат
.
В самом деле, если возвести обе части
равенства (17) в квадрат
![]() (18)
(18)
и разделить почленно на равенство (10), получим:
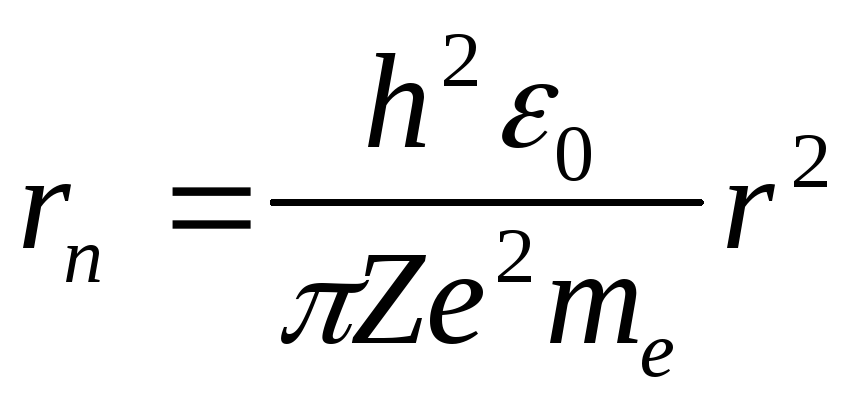 .
(19)
.
(19)
Подставка
найденного значения
![]() в формулу (14) приводит к выражению:
в формулу (14) приводит к выражению:
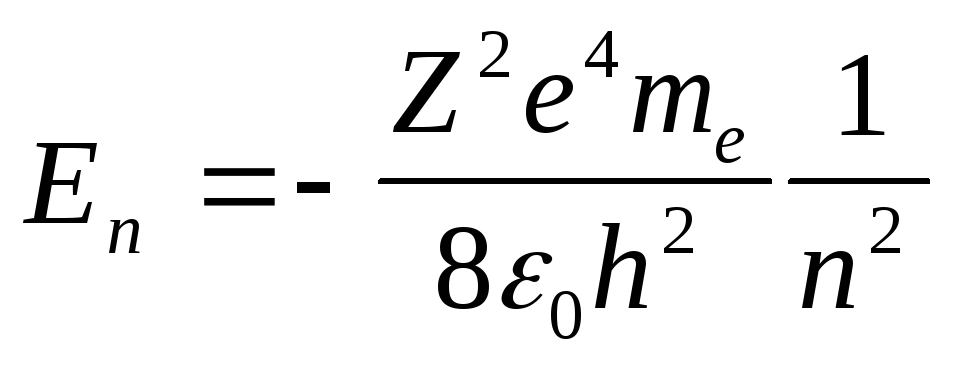 .
(20)
.
(20)
Заменив в этом выражении знак n на m , найдем:
![]() .
(21)
.
(21)
Знак минус в формулах (20) и (21) означает притяжение электрона к ядру.
Теперь
остается подставить найденные значения
![]() и
и
![]() в формулу (7) при этом получается ФОРМУЛА
БОРА ДЛЯ СПЕКТРОВ ВОДОРОДНОПОДОБНЫХ
АТОМОВ:
в формулу (7) при этом получается ФОРМУЛА
БОРА ДЛЯ СПЕКТРОВ ВОДОРОДНОПОДОБНЫХ
АТОМОВ:
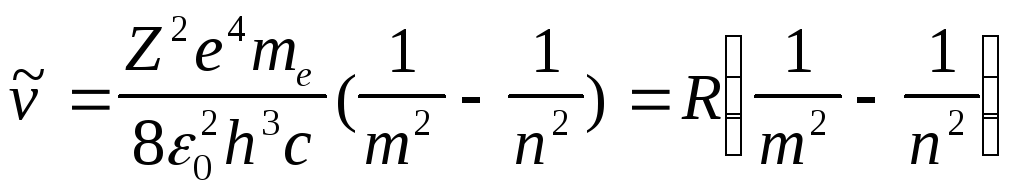 ,
(22)
,
(22)
где положено
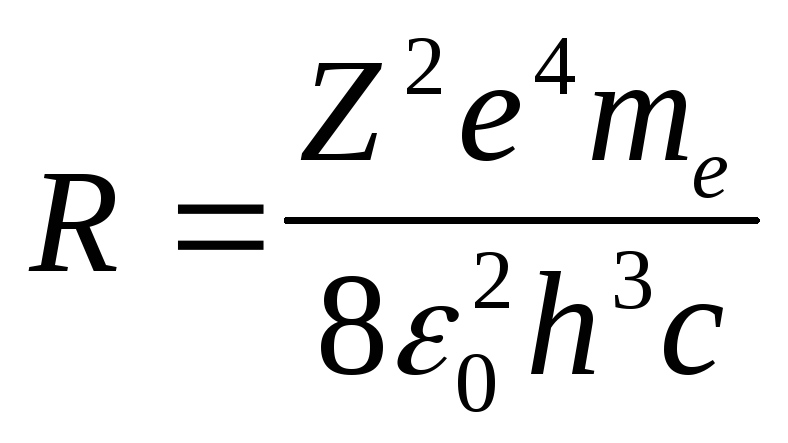 .
(23)
.
(23)
