АНАЛИЗ ЧЕТЫРЕХПОЛЮСНИКОВ И ДВУХПОЛЮСНИКОВ КАСКАДНОЙ СТРУКТУРЫ С ПОМОЩЬЮ МАТРИЦ ПЕРЕДАЧИ
Многие четырехполюсные и двухполюсные устройства СВЧ имеют каскадную структуру, для которой характерно, что выход предшествующего четырехполюсника является входом последующего и т. д. (рис. 4.1).
Анализ такого соединения значительно упрощается, если характеризовать четырехполюсники, а также их объединение специальными матрицами – матрицами передачи. При определении матриц передачи в качестве воздействия на четырехполюсник выбирается пара электрических величин, определяющих режим одного входа (обычно второго), а в качестве реакции – соответствующая пара величин, определяющая режим другого входа (обычно первого).
Для классической матрицы передачи А связь воздействия и реакции имеет вид
(4.1)
При таком определении матрица передачи любого числа каскадно включенных четырехполюсников оказывается равной произведению матриц передачи отдельных каскадов – это основное свойство любой матрицы передачи. Перемножать матрицы каскадов надо именно в той последовательности, в какой они включены в тракт.
Иногда предпочитают пользоваться так называемой волновой матрицей передачи, вводимой соотношениями
Каких-либо дополнительных возможностей по сравнению с матрицей А матрица Т не дает.
Из (4.1) следует, что элементы 
матрицы А представляют собой коэффициенты передачи по нормированному напряжению и нормированную взаимную проводимость при холостом ходе на выходе 2 четырехполюсника. Элементы 
– коэффициент передачи по нормированному току и нормированное взаимное сопротивление при коротком замыкании на выходе 2.
Зная элементы матрицы А, легко анализировать двухполюсники каскадной структуры, образующиеся при нагружении последнего каскада устройством с
нормированным сопротивлением 
.
Входное сопротивление такого составного двухполюсника будет
(4.2)
где использованы элементы матрицы
.
Если оконечная нагрузка представляет короткое замыкания или разрыв, то формула (4.2) упрощается и принимает одну из следующих форм: 
(4.3)
Коэффициент отражения составного двухполюсника можно найти по обычной формуле
через полное входное сопротивление
.
Связь матрицы А с матрицей рассеяния четырехполюсника.
Для получения формул перехода от матрицы передачи к матрице рассеяния 
следует выразить столбцы воздействия и реакции в (4.1) через падающие и отраженные волны:
и
После преобразования получаем формулы перехода:
(4.5)
Условия реактивности четырехполюсника.
Из формул перехода к матрице рассеяния (4.5) следует, что требование взаимности 
приводит к равенству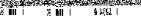 
Таким образом, для взаимных четырехполюсников определитель матрицы передачи должен быть равен единице.
Далее, из условия отсутствия потерь во взаимном четырехполюснике следует, что в матрице передачи элементы 
должны быть чисто вещественны-
ми, а элементы 
– чисто мнимыми. Это свойство легко обобщить на каскадное соединение любого числа таких четырехполюсников. Для невзаимных четырехполюсников условие недиссипативности более сложное и сводится к представимости матрицы передачи в виде
, где 
и 
– вещественные числа.
Условия симметрии и антиметрии четырехполюсников.
Для симметричных четырехполюсников должны выполняться равенства 
С помощью формул перехода (4.5) легко установить, что симметрия имеет место при выполнении условий на элементы матрицы передачи:
Своего рода противоположностью симметричным четырехполюсникам являются так называемые антиметричные четырехполюсники, т. е. такие, у которых на любой частоте собственные коэффициенты отражения двух входов равны по значению и противоположны по фазе: 
и 
Из формул перехода (4.5) следует, что в терминах матрицы передачи условия антиметрии сводятся к равенствам
и 
Антиметричным является стык двух линий передачи, остальные элементарные четырехполюсники симметричны.
МЕТОД ДЕКОМПОЗИЦИИ СИММЕТРИЧНЫХ ВОСЬМИПОЛЮСНИКОВ (МЕТОД СИНФАЗНОГО И ПРОТИВОФАЗНОГО ВОЗБУЖДЕНИЯ)
Этот метод сводит анализ восьмиполюсников, имеющих плоскость симметрии, к анализу более простых четырехполюсников, представляющих собой «половины» восьмиполюсника.
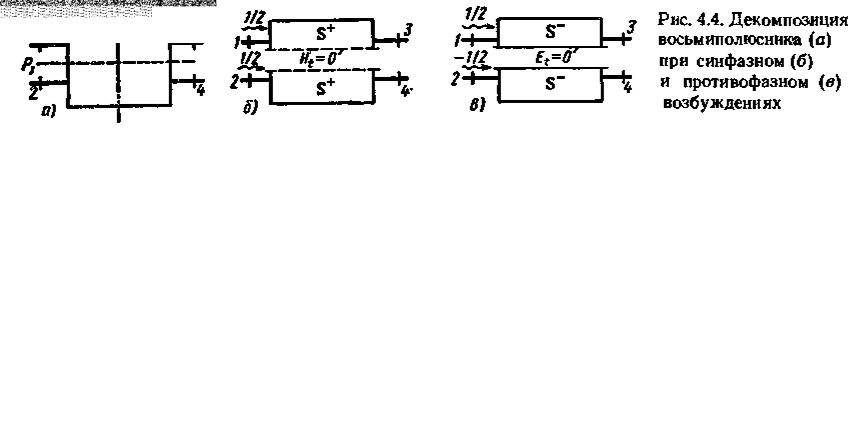
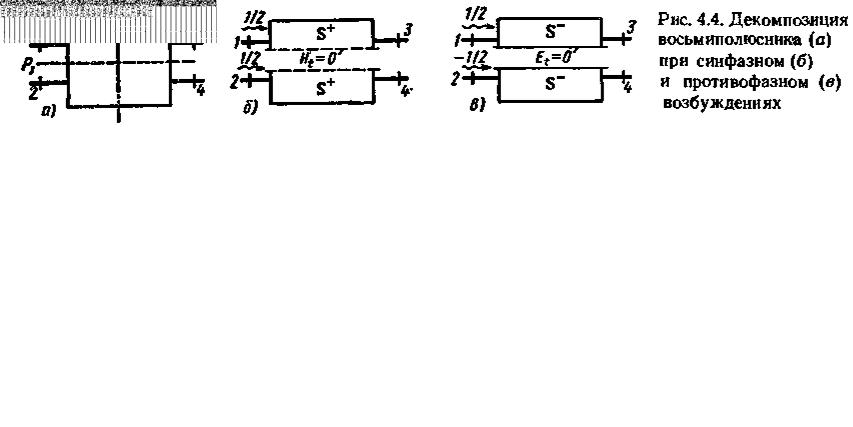
Пусть плоскость симметрии взаимного восьмиполюсника проходит между входами 1, 3 и 2, 4 (рис. 4.4, а). В матрице рассеяния восьмиполюсника вслед-
ствие симметрии и взаимности независимыми между собой оказываются только шесть элементов:
и
Рассмотрим два режима возбуждения восьмиполюсника: синфазный и противофазный.
1.При синфазном возбуждении со стороны входов 1 и 2 падающими волнами
=1/2, 
=1/2 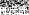через плоскость симметрии не происходит передачи мощности и в ней устанавливается пучность распределения напряженности касательного электрического поля и нуль распределения напряженности касательного магнитного поля, т. е. создается режим холостого хода. Плоскость как бы расчленяет восьмиполюсник на два не связанных между собой парциальных четырехполюсника синфазного возбуждения, каждый из которых характеризуется матрицей рассеяния 
(рис. 4.4, б).
2.При противофазном возбуждении со стороны входов 1 и 2 падающими волнами 
=1/2, 
= –1/2 через плоскость симметрии нет передачи мощности, в этой плоскости устанавливается нуль распределения напряженности касательного электрического поля и пучность распределения напряженности касательного магнитного поля, т. е. создается режим короткого замыкания. Плоскость симметрии как бы расчленяет восьмиполюсник на два не связанных между собой парциальных четырехполюсника противофазного возбуждения, каждый из которых характеризуется матрицей рассеяния 
(рис. 4.4, в).
Матрицы рассеяния парциальных четырехполюсников синфазного и противофазного возбуждения
могут быть определены одна независимо от другой, например, через произведение матриц передачи, если парциальные четырехполюсники представимы в виде цепочки элементарных каскадов.
Суперпозиция синфазного и противофазного возбуждения входов 1 и 2 в восьмиполюснике представляет возбуждение одиночного входа 1:
Поэтому, суммируя реакции парциальных четырехполюсников на синфазное и противофазное возбуждения входов 1 и 2, можно определить следующие четыре независимых элемента матрицы рассеяния восьмиполюсника:
(4.8)
Для нахождения элементов 
матрицы 
восьмиполюсника достаточно повторить опыты синфазного и противофазного возбуждения для входов 3
и 4. Это приводит к искомым соотношениям 
(4.8а)
При наличии у восьмиполюсника еще одной плоскости симметрии (или при наличии полной поворотной симметрии всех четырех входов) с помощью
формул (4.8а) будет автоматически получено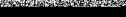 
Описанный метод синфазного и противофазного возбуждения может быть обобщен на симметричные многополюсники с любым четным числом входов.
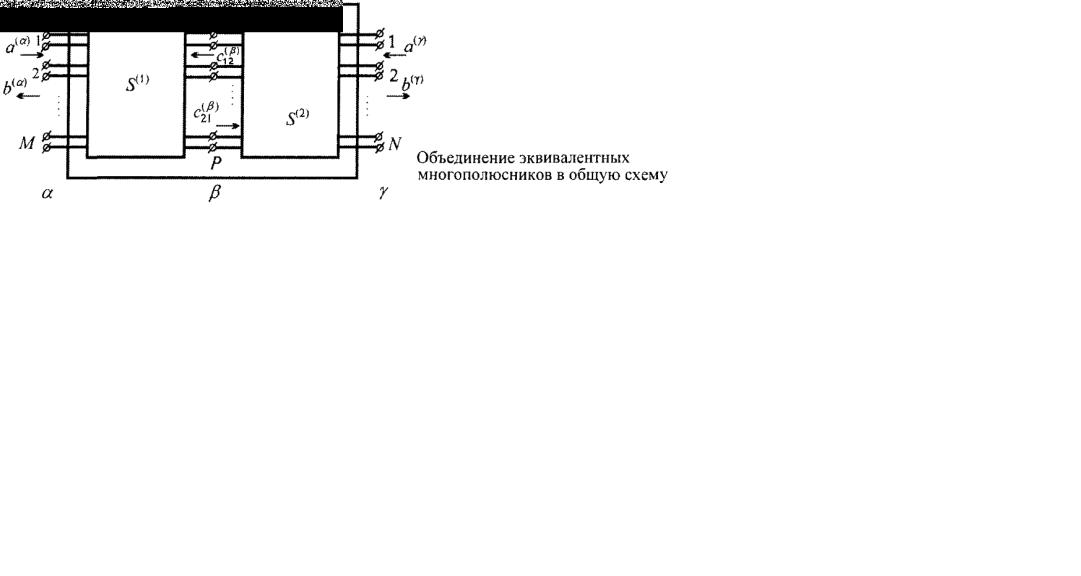
Объединение устройств СВЧ в общую схему
Рассмотрим два устройства СВЧ (или базовых элемента), матрицы рассеяния которых известны и равны 
соответственно. В результате образуется
более сложное устройство СВЧ с результирующей матрицей рассеянии
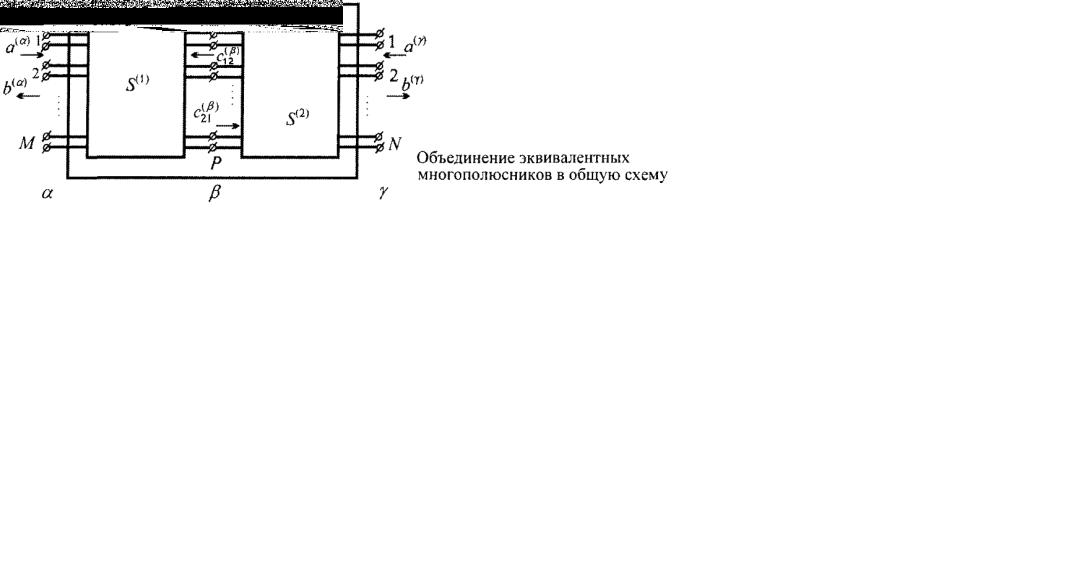
Требуется определить эту матрицу по известным матрицам 
Эквивалентная многополюсная схема соединения показана на рисунке. Следует отметить, что соединять можно лишь те клеммы многополюсников, которые соответствуют одинаковым типам линий передачи с одинаковыми размерами поперечного сечения. В противном случае в месте соединения образуется стык различных линий передачи, который на эквивалентной схеме также отображается в виде многополюсника, подлежащего объединению.
На рис. 6.1 клеммы эквивалентных многополюсников представлены в виде трех групп.
Впервую группу входят М пар клемм, эквивалентных свободным необъединяемым входам первого устройства СВЧ. Эта группа клемм отображена как клеммная плоскость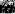 
Вэтой клеммной плоскости определены столбцы амплитуд падающих 
и отраженных 
волн:
Во вторую группу входят Р пар клемм, эквивалентных соединенным входам первого и второго устройств СВЧ. Она отображена как клеммная плоскость
В этой клеммной плоскости определены столбцы 
и 
амплитуд волн, распространяющихся навстречу друг другу. Столбец 
составлен из ам-
плитуд волн, бегущих из второго многополюсника в первый, а столбец 
– из амплитуд волн, бегущих из первого многополюсника во второй. Каждый из этих столбцов можно рассматривать как столбец амплитуд падающих или отраженных волн по отношению к соответствующему многополюснику.
Например, 
можно рассматривать как столбец амплитуд падающих волн со стороны клеммной плоскости 
по отношению к первому многополюснику. Но он же является столбцом амплитуд отраженных волн по отношению ко второму многополюснику.
Втретью группу входят N пар клемм, эквивалентных свободным необъединяемым входам второго устройства СВЧ. Эта группа клемм отображена как клеммная плоскость 
где определены столбцы амплитуд падающих 
и отраженных 
волн:
Всоответствии с выделенными клеммными плоскостями матрицы рассеяния 
и 
первого и второго устройств СВЧ могут быть представлены в блочном виде:
(6.1)
где 
– квадратная матрица порядка М, элементы которой определяют коэффициенты отражения и взаимосвязи входов, соответствующих клеммной плоскости 
– прямоугольная матрица размером 
элементы которой определяют коэффициенты передачи со входов клеммной плоскости 
на входы клеммной плоскости 
– квадратная матрица порядка Р, элементы которой определяют коэффициенты отражения и взаимосвязи входов клеммной плоскости 
первого многополюсника.
Аналогичный смысл имеют блоки матрицы 
Таким образом, 
есть квадратная матрица порядка Р+М, а 
– квадратная матрица порядка Р+N. Результирующая матрица рассеяния 
связывает столбцы амплитуд падающих и отраженных волн на входах объединенного устройства СВЧ:
(6.2)
где 
– столбец амплитуд падающих волн, составленный из элементов столбцов 
и 
;
– столбец амплитуд отраженных волн, составленный из элементов столбцов 
и 
. Соотношение (6.2) может быть представлено в блочном виде:
(6.3)
или в виде двух матричных уравнений, вытекающих из (6.3):
(6.4)
Используя схему объединения многополюсников (см. рис. 6.1) и блочный вид матриц 
(6.1), составляем уравнения, определяющие столбцы 
через 
(6.5)
Далее исключают из уравнений 
и привводят их к виду, аналогичному (6.4). Тогда матричные коэффициенты при столбцах 
определяют соответствующие блоки результирующей матрицы 
.
Аналогично Подставляя найденные столбцы 
в первое и четвертое уравнения (6.5), получаем
(6.6)
Найдены все блоки результирующей матрицы 
выраженные через блоки матриц 
Данные соотношения лежат в основе алгоритмов вычисления характеристик сложных устройств СВЧ с помощью ЭВМ. При использовании этих соот-
ношений возникает необходимость обращения матриц, порядок которых равен числу объединяемых входов. При большом числе объединяемых входов время обращения матриц на ЭВМ может стать недопустимо большим, а точность обращения недостаточной. Поэтому при объединении устройств СВЧ в общую схему для увеличения точности расчетов часто используется алгоритм, при котором на каждом шаге вычислений объединяются только два входа устройства СВЧ. Это приводит к обращению матриц второго порядка, что выполняется аналитически.
Соотношения (6.6) существенно упрощаются, если некоторые блоки матриц 
или 
равны нулю.
В практических расчетах характеристик идеальных устройств СВЧ часто блоки 
и 
равны нулю. Такие устройства являются согласованными по всем входам. Кроме того, отсутствует взаимосвязь между входами в каждой из выделенных клеммных плоскостей. Говорят, что входы в этих
клеммных плоскостях развязаны. В этом случае соотношения (6.6) принимают вид 
При объединении устройств СВЧ, соответствующем каскадному соединению многополюсников с согласованными и развязанными входами в клеммных
плоскостях, результирующий многополюсник также имеет согласованные и развязанные входы, а блоки коэффициентов передачи между клеммными плоскостями определяются перемножением соответствующих блоков исходных многополюсников.
Проекционные методы анализа устройств СВЧ
Для анализа сложных устройств СВЧ на основе принципа декомпозиции необходимо уметь вычислять матрицы внешних характеристик базовых элементов. Вычисление этих матриц проводится с помощью соотношений, получающихся в результате решения уравнений Максвелла применительно к конкретным граничным условиям, задаваемым геометрической структурой конкретного базового элемента. При этом в результате решения уравнений электродинамики должна быть составлена математическая модель базового элемента, позволяющая определять матрицы его внешних характеристик. Для составления математической модели могут быть использованы различные методы, однако наибольшее практическое применение получили проекционные методы.
Суть проекционных методов состоит в том, что неизвестные поля, являющиеся элементами функционального пространства, проецируются с помощью полной ортонормированной системы функций в числовое пространство. При этом неизвестным становится множество чисел, являющихся коэффициентами базисных функций, совокупность которых определяет неизвестные поля.
Роль базисных функций во внутренних задачах электродинамики обычно играют поля различных типов волн волноводов или резонаторов. К проекционным методам относятся: метод Галёркина, метод моментов, метод частичных областей, метод коллокаций и т.п.
В качестве примера рассмотрим подробнее основную идею метода Галёркина.
Предположим, что решается краевая задача для области 
ограниченной замкнутой поверхностью 
сформулированная в виде операторного уравнения
(6.7)
где 
– некоторый электродинамический оператор; 
– подлежащая определению векторная, функция;
– известная векторная функция, определяющая внешнее возбуждение в рассматриваемой задаче.
Функция 
обычно задается в виде касательных составляющих полей на части поверхности
являющейся поверхностью клеммных плоскостей устройства СВЧ (поперечными сечениями входных линий передачи).
Функция 
представляет собой неизвестное электрическое или магнитное поле внутри устройства СВЧ.
При решении внутренних задач обычно находится полная ортонормированная в объеме 
система функций 
которая может служить базисом для представления неизвестной функции 
рядом Фурье:
(6.8)
Полнота системы функций 
означает, что при любом внешнем воздействии 
неизвестная функция 
представима в виде ряда (6.8). Ортонормированность функций 
означает удовлетворение их условию
(6.9)
С учетом этого из (6.8) имеем
Из (6.7) следует, что 
есть нулевой элемент функционального пространства, поэтому он ортогонален к любой функции базиса:
(6.10)
В методе Галёркина искомое приближенное решение представляется в виде линейной комбинации первых 
базисных функций (в виде усеченного ряда
Фурье) с неопределенными коэффициентами:
(6.11)
Это приближенное решение подчиняется условию ортогональности, аналогичному (6.10), т.е.
Подставляя сюда (6.11) с учетом (6.9), получаем систему N линейных уравнений относительно коэффициентов 
которая может быть записана в виде: 
,
где А – квадратная матрица порядка 
с коэффициентами 
– столбец неизвестных коэффициентов;
– столбец свободных членов, элементы которого определяются уравнением 
.
Таким образом, метод Галёркина, как и другие проекционные методы, сводит неоднородную краевую задачу к неоднородной системе линейных уравнений, решение которой определяет коэффициенты разложения искомой функции. При этом чем выше порядок системы, т.е. чем больше N, тем точнее определяется неизвестная функция 
.
Определив с помощью этого метода поля внутри базового элемента, а, следовательно, и в поперечных сечениях его входных линий передачи, можно найти численные значения напряжений и токов на клеммах эквивалентного многополюсника, используя, например, соотношение (6.1). По токам и напряжениям на клеммах многополюсника могут быть найдены любые матрицы внешних характеристик базового элемента.
Объединив матрицы рассеяния базовых элементов в общую схему, можно найти матрицу рассеяния сложного устройства СВЧ и вычислить любые его характеристики. Эти вычисления проводятся с применением высокопроизводительных ЭВМ.
МЕТОД ДЕКОМПОЗИЦИИ СИММЕТРИЧНЫХ ВОСЬМИПОЛЮСНИКОВ (МЕТОД СИНФАЗНОГО И ПРОТИВОФАЗНОГО ВОЗБУЖДЕНИЯ)
Этот метод сводит анализ восьмиполюсников, имеющих плоскость симметрии, к анализу более простых четырехполюсников, представляющих собой «половины» восьмиполюсника.
Пусть плоскость симметрии взаимного восьмиполюсника проходит между входами 1, 3 и 2, 4 (рис. 4.4, а). В матрице рассеяния восьмиполюсника вслед-
ствие симметрии и взаимности независимыми между собой оказываются только шесть элементов:
и
Рассмотрим два режима возбуждения восьмиполюсника: синфазный и противофазный.
1.При синфазном возбуждении со стороны входов 1 и 2 падающими волнами
=1/2, 
=1/2 через плоскость симметрии не происходит передачи мощности и в ней устанавливается пучность распределения напряженности касательного электрического поля и нуль распределения напряженности касательного магнитного поля, т. е. создается режим холостого хода. Плоскость как бы расчленяет восьмиполюсник на два не связанных между собой парциальных четырехполюсника синфазного возбуждения, каждый из которых характеризуется матрицей рассеяния 
(рис. 4.4, б).
2.При противофазном возбуждении со стороны входов 1 и 2 падающими волнами 
=1/2, 
= –1/2 через плоскость симметрии нет передачи мощности, в этой плоскости устанавливается нуль распределения напряженности касательного электрического поля и пучность распределения напряженности касательного магнитного поля, т. е. создается режим короткого замыкания. Плоскость симметрии как бы расчленяет восьмиполюсник на два не связанных между собой парциальных четырехполюсника противофазного возбуждения, каждый из которых характеризуется матрицей рассеяния 
(рис. 4.4, в).
Матрицы рассеяния парциальных четырехполюсников синфазного и противофазного возбуждения
могут быть определены одна независимо от другой, например, через произведение матриц передачи, если парциальные четырехполюсники представимы в виде цепочки элементарных каскадов.
Суперпозиция синфазного и противофазного возбуждения входов 1 и 2 в восьмиполюснике представляет возбуждение одиночного входа 1:
Поэтому, суммируя реакции парциальных четырехполюсников на синфазное и противофазное возбуждения входов 1 и 2, можно определить следующие четыре независимых элемента матрицы рассеяния восьмиполюсника:
(4.8)
Для нахождения элементов 
матрицы 
восьмиполюсника достаточно повторить опыты синфазного и противофазного возбуждения для входов 3
и 4. Это приводит к искомым соотношениям 
(4.8а)
При наличии у восьмиполюсника еще одной плоскости симметрии (или при наличии полной поворотной симметрии всех четырех входов) с помощью
формул (4.8а) будет автоматически получено 
Описанный метод синфазного и противофазного возбуждения может быть обобщен на симметричные многополюсники с любым четным числом входов.
Объединение устройств СВЧ в общую схему
Рассмотрим два устройства СВЧ (или базовых элемента), матрицы рассеяния которых известны и равны 
соответственно. В результате образуется
более сложное устройство СВЧ с результирующей матрицей рассеянии
Требуется определить эту матрицу по известным матрицам 
Эквивалентная многополюсная схема соединения показана на рисунке. Следует отметить, что соединять можно лишь те клеммы многополюсников, которые соответствуют одинаковым типам линий передачи с одинаковыми размерами поперечного сечения. В противном случае в месте соединения образуется стык различных линий передачи, который на эквивалентной схеме также отображается в виде многополюсника, подлежащего объединению.
На рис. 6.1 клеммы эквивалентных многополюсников представлены в виде трех групп.
Впервую группу входят М пар клемм, эквивалентных свободным необъединяемым входам первого устройства СВЧ. Эта группа клемм отображена как клеммная плоскость 
Вэтой клеммной плоскости определены столбцы амплитуд падающих 
и отраженных 
волн:
Во вторую группу входят Р пар клемм, эквивалентных соединенным входам первого и второго устройств СВЧ. Она отображена как клеммная плоскость
В этой клеммной плоскости определены столбцы 
и 
амплитуд волн, распространяющихся навстречу друг другу. Столбец 
составлен из ам-
плитуд волн, бегущих из второго многополюсника в первый, а столбец 
– из амплитуд волн, бегущих из первого многополюсника во второй. Каждый из этих столбцов можно рассматривать как столбец амплитуд падающих или отраженных волн по отношению к соответствующему многополюснику.
Например, 
можно рассматривать как столбец амплитуд падающих волн со стороны клеммной плоскости 
по отношению к первому многополюснику. Но он же является столбцом амплитуд отраженных волн по отношению ко второму многополюснику.
Втретью группу входят N пар клемм, эквивалентных свободным необъединяемым входам второго устройства СВЧ. Эта группа клемм отображена как клеммная плоскость 
где определены столбцы амплитуд падающих 
и отраженных 
волн:
Всоответствии с выделенными клеммными плоскостями матрицы рассеяния 
и 
первого и второго устройств СВЧ могут быть представлены в блочном виде: