масштаба 1:1000000 в зонах от 0 до 400 м применяется высота сечения рельефа 50 м, от 400 до 1000 м – 100 м, выше 1000 м – 200 м.

С учетом характера местности и для карт масштабов 1:100000 – 1:500000 могут применяться и другие значения высоты сечения рельефа, как в сторону ее уменьшения, так и в сторону увеличения.

В некоторых случаях, при решении специальных задач, устанавливают высоты сечения рельефа, определяемые техническим заданием. Это может относиться как к рельефу местности, так и к рельефу поверхности каких-либо объектов.

§ 17. Ориентирование

Ориентирование линии на местности или топографической карте заключается в определении ее направления относительно исходного или известного направления.

За исходное направление в геодезии принимают направления следующих меридианов:

-истинного меридиана, определяемого касательной к истинному меридиану в данной точке;

-осевого меридиана, являющегося в проекции Гаусса прямой линией,

параллельной оси х прямоугольных координат и вертикальным линиям километровой сетки карты;

- магнитного меридиана, определяемого касательной к линии пересечения с поверхностью Земли плоскости, проходящей через ось магнитной стрелки компаса и отвесную линию в данной точке.

Ориентирующим углом в общем случае является горизонтальный угол

(угол между направлениями в горизонтальной плоскости), который отсчитывают по часовой стрелке от северного направления меридиана до направления линии в данной точке.

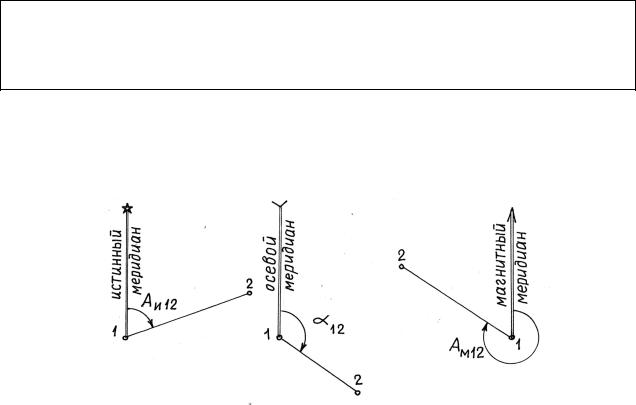
Таким образом, существует три ориентирующих угла (рис. 2.17): при использовании истинного меридиана – истинный азимут (АИ); при использовании осевого меридиана – дирекционный угол (α); при использовании магнитного меридиана – магнитный азимут (АМ).

Рис. 2.17. Ориентирующие углы

41

Основываясь на данном выше определении ориентирующего угла, запишем следующее определение для каждого из названных ориентирующих углов.

Истинным азимутом (дирекционным углом, магнитным азимутом) называется горизонтальный угол, отсчитываемый от северного направления истинного (осевого, магнитного) меридиана по часовой стрелке до направления линии в данной точке.

Ориентирующий угол изменяется от 0о до 360о. Знак «плюс» или «минус» у ориентирующих углов не предусматривается. Если значение ориентирующего угла получится в расчетах больше, чем 360о, то из полученного значения следует вычесть 360о столько раз, пока значение ориентирующего угла не станет в пределах полного круга. Если в расчетах значение ориентирующего угла получится отрицательным, то необходимо к полученной его величине прибавить 360о.

Движение по линии АВ может быть прямым и обратным. Принимая, например, направление АВ прямым, движение по направлению ВА следует считать обратным. И наоборот. В соответствии с этим существуют прямой и обратный ориентирующие углы А (АИ , α , АМ ), связанные соотношением:

Вформулах (2.15) и (2.16) перед 180о может стоять знак «плюс-минус» .

Знак «плюс» берется в том случае, если от АПР или АОБР нельзя отнять 180о. Но можно и оставить только знак «плюс», как в приведенных формулах. Результат от этого не изменится. Проверьте это сами на любом примере.

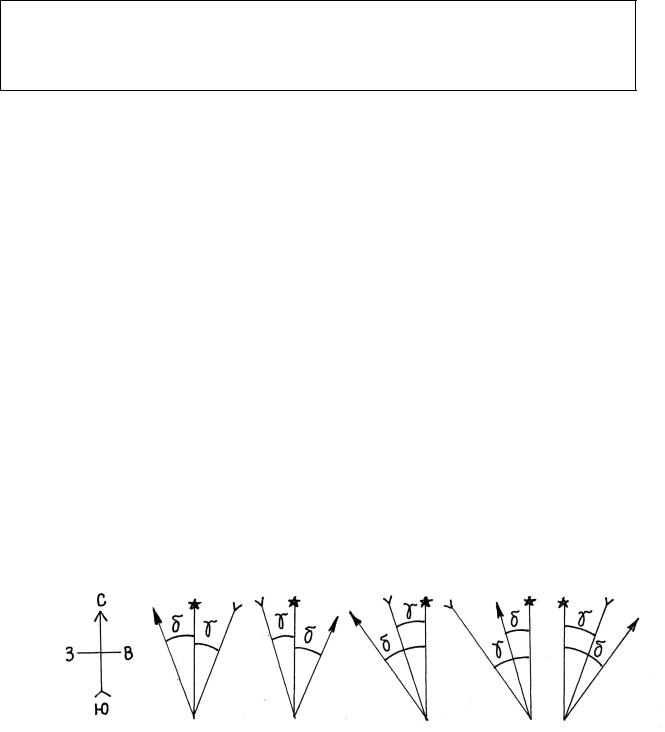
Вобщем случае для любой точки на поверхности земного эллипсоида существует три исходных направления, взаимное расположение которых друг относительно друга может быть различным. На рис. 2.18 показано несколько возможных вариантов взаимного расположения векторов исходных меридианов.

Рис. 2.18. Взаимосвязь ориентирющих углов.

Зная ориентирующий угол какой-либо линии и углы между направлениями меридианов, можно ориентировать линию по другому исходному направлению.

Направление любого меридиана на земном эллипсоиде (или референцэллипсоиде) определяется направлением касательной к меридиану в данной точке. Касательная к истинному меридиану называется полуденной линией

42

(см. рис. 2.6). Полуденные линии, построенные для точек экватора, параллельны друг другу, на северном и южном полюсах полуденные линии перпендикулярны к оси вращения и все лежат в горизонтальной плоскости. В других случаях они пересекаются в точке, лежащей на оси вращения Земли. Полуденные линии точек, лежащих на одной и той же параллели, т.е. имеющих одну и ту же широту, пересекаются в одной точке на оси вращения Земли.

Угол между направлениями истинных меридианов называется сближением меридианов. Угол γ (рис. 2.18) между направлением истинного меридиана и направлением осевого меридиана называется гауссовым сближением меридианов. Такими углами пользуются при работе в соответствующей зоне. Для сокращения и в этом случае применяют название

сближение меридианов. При этом

направлениями полуденных линий истинного меридиана точки и осевого

φ – географическая широта точки (определяется как среднее значение широт для точек 1 и 2). Если требуется определить сближение меридианов для точки 1 относительно точки 2, то в формуле (2.18) берут значение широты для точки 1.

Поскольку долгота λ2 в зоне соответствует долготе осевого меридаина, то

φ – географическая широта точки i.

Сближение меридианов в зоне для какой-либо точки местности может быть положительным (восточным) или отрицательным (западным), а также и равным нулю, если точка будет находиться на осевом меридиане зоны (или на экваторе).

Точность определения сближения меридианов по формуле (2.19) составляет 0,1 угловых минуты.

Пример 2.8. Известна долгота точки λ = 13о45΄ и ее широта φ = 56о18΄. Определить сближение меридианов точки относительно осевого меридиана зоны.

Решение.

В соответствии со своей долготой точка находится в третьей зоне, ограниченной меридианами 12о и 18о. Осевой меридиан зоны имеет долготу 15о- см. формулу (2.7).

γ= (13о45΄ - 15о00΄) sin 56о18΄ = (- 1о15΄) sin 56о18΄ = (- 75΄) sin 56о18΄= - 62,3966΄ =

=-1о02΄. (В приведенных расчетах достаточно округления до 1΄).

Ответ. Сближение меридианов западное 1о02΄.

Взаимосвязь истинного и магнитного азимутов определяется углом δ, который называется магнитным склонением. Магнитное склонение может быть западным (отрицательным) и восточным (положительным), что на сетке

43

меридианов (рис. 2.18) отражено в виде отклонения магнитного меридиана относительно истинного соответственно на запад или восток (по аналогии со сближением меридианов). Формула взаимосвязи истинного и магнитного азимутов имеет вид:

Как известно, полюсы магнитного поля Земли находятся в постоянном движении. Впервые склонение магнитной стрелки обнаружил Х.Колумб (в 1492 г.) во время своего первого плавания к берегам Америки. Величина магнитного склонения подвержена суточным, годовым и вековым колебаниям. В результате исследований установлено, что за 500 лет склонение магнитной стрелки изменяется примерно на 22о. В 1600 г., например, северный магнитный полюс находился на расстоянии 1300 км от географического полюса. Сейчас это расстояние составляет 2000 км. Суточные изменения склонения сравнительно небольшие, до 10΄, максимальные значения могут достигать 15΄. Известно время, когда ось магнитной стрелки не имеет суточного склонения : 4 и 10 часов утра, 20 часов вечера и 24 часа. Кроме того, само магнитное поле искажается под действием магнитных бурь. Северный и южный магнитные полюсы находятся сравнительно далеко от географических: северный магнитный полюс (долгота 97о западная, широта 75о северная); южный магнитный полюс (долгота 154о восточная, широта 72о южная).

На топографических картах указывают т.н. годовое изменение магнитного склонения (Δδ), а саму величину магнитного склонения указывают на год издания топографической карты. Для определения магнитного

В формуле (2.21): t1 и t2 – соответственно год издания топографической карты и год, в котором производится определение текущего значения магнитного склонения δ2 по его известной величине δ1 и годовому изменению δ.

На топографической карте на год ее издания наносят сетку меридианов с величинами сближения меридианов и магнитного склонения. В текстовой части приводят значение годового изменения магнитного склонения.

При использовании топографической карты и компаса для перехода от магнитного азимута к дирекционному углу определяют величину поправки α в дирекционный угол, определяемой как горизонтальный угол между

Если стрелка компаса отклонена от осевого меридиана на запад, то поправка в дирекционный угол имеет знак «минус», если стрелка отклонена от направления осевого меридиана на восток, то поправка имеет знак «плюс».

Пример 2.9. На топографической карте измерен дирекционный угол α =123о40΄. Сближение меридианов восточное 1о43΄. Склонение магнитной стрелки на 1994 г. западное 4о33΄. Годовое изменение магнитного склонения восточное δ = 0о06΄.

Определить истинный азимут, магнитный азимут на 2000 г. и поправку в дирекциионный угол при переходе от магнитного азимута к дирекционному углу также в 2000 г.

Решение.

Вычисляем магнитное склонение на 2000 г.

δ 2000 = δ1994 + δ ( 2000 – 1994 ) = - 4о33΄ + 0о06΄ х 6 = - 3о57΄. Величина истинного азимута равна

44

АИ = α + γ = 123о40΄ + 1о43΄ = 125о23΄.

Значение магнитного азимута на 2000 год находим по формуле (2.19), преобразованной для магнитного азимута:

АМ 2000 = АИ – δ2000 = 125о23΄ - (- 3о57΄) = 129о20΄.

Поправка в дирекционный угол α = - 3о57΄ - 1о43΄ = - 5о40΄.

Поскольку сближение меридианов на карте указывают для ее центра, то в общем случае сближение меридианов произвольной точки карты будет отличаться от сближения меридианов для центральной точки карты. При необходимости можно вычислить для заданной точки частное сближение меридианов по формуле (2.19), а затем использовать полученное значение в дальнейших расчетах. Кроме того, поскольку сближения меридианов точек, находящихся на концах линии, в общем случае могут отличаться друг от друга, то значения прямого и обратного азимутов данной линии будут отличаться от 180о.

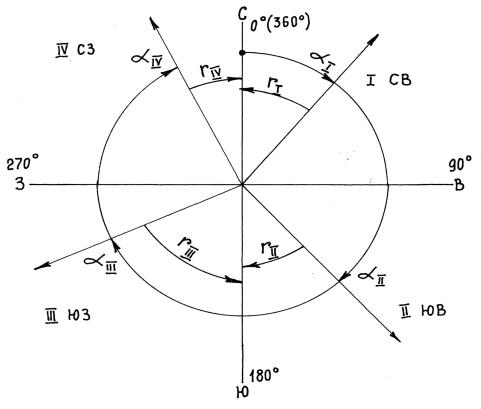
Для ориентирования линий часто используется четвертная система (рис. 2.19), ориентирование в которой производится как по величине горизонтального угла (румба), так и по указанию той или иной четверти по сторонам света.

Румб (r) – это острый горизонтальный угол между направлением линии и ближайшим направлением меридиана.

Румб записывают в следующем виде: r = ЮВ:43о32΄, r = СЗ:17о04΄ и т.п. Значение румба изменяется от 0о до 90о.

Рис. 2.19. Четвертная система ориентирования

Слово румб произошло от греческого слова «roumb». Такой геометрической фигурой изображались 32 направления на картушке (горизонтальном круге) магнитного компаса.

45