Рис. 10.18. Переходная кривая

где С – параметр кривой (постоянный коэффициент; его выбирают в пределах 45000 – 150000 в зависимости от скорости движения поезда; при небольших скоростях С < 45000); Li – длина переходной кривой до точки i; ρi – радиус кривизны кривой в указанной точке.

Значения стрелок прогиба через определенный шаг вычисляют от стягивающей хорды с учетом параметров переходной кривой. Поскольку переходная кривая несимметричная, то величины стрелок прогиба будут различными, т.е. разбивку следует выполнять нарастающим итогом либо от НПК (начала переходной кривой), либо от ее конца (КПК). Для определения стрелок прогиба переходных кривых существуют специальные таблицы.

Способ стягивающей хорды является более точным из всех, рассмотренных выше, поскольку значения промеров bi значительно меньше, чем промеры от тангенса.

§ 102. Разбивка фундаментов инженерных сооружений

Базовые (главные) оси сооружения закрепляют на местности постоянными знаками, которые устанавливают ниже глубины промерзания грунтов. Каждая из осей должна иметь не менее четырех знаков, по два на обеих ее сторонах. Остальные оси могут быть закреплены временными знаками по два знака на каждую из осей (рис. 10.19).

Для удобства использования на строительной площадке все оси, либо основную их часть, выносят на обноску. Обноской является доска, горизон-

289

тально закрепленная на столбах (стойках) на высоте примерно 0,5 м от поверхности земли. Существует и металлическая обноска многоразового использования. Ось на обноске фиксируют гвоздем. На металлической обноске имеется специальный хомут, который может в открепленном состоянии свободно передвигаться по обноске.

Рис. 10.19. Закрепление осей строящегося здания

Рис. 10.20. Разбивка фундамента

Реже применяют сплошную обноску из-за ее громоздкости и сложности построения. Сполошная обноска выполняется прямолинейной, устанавливается строго параллельно основным осям по всему контуру здания, в связи с чем от нее можно непосредственно откладывать проектные расстояния. Створная обноска устанавливается фрагментами, в местах расположения осей, причем, на произвольных расстояниях от контура здания.

Створная обноска применяется и при разбивке фундаментов (рис. 10.20).

290

В этом случае одна из меток на обноске определяет положение габаритной (основной) оси строения, а вторую метку устанавливают в соответствии с проектными размерами фундамента. По меткам натягивают проволоку на соответствующую другую обноску и определяют положение контура фундамента по проекции проволоки на земле.

§ 103. Оценка точности разбивочных работ

На точность разбивочных работ влияют погрешности из-за центрирования прибора и визирных целей (mЦ), погрешности фиксации точки на местности или конструкции сооружения (mФ ), погрешности собственно разбивочных работ (mРР), которые зависят от геометрии способа разбивки, а также погрешности исходных данных (mИСХ), зависящие от точности определения координат геодезической разбивочной основы. При этом погрешности mИСХ и mЦ определяются и геометрией способа разбивки. С учетом этого, общая погрешность разбивки (mР) определится суммой всех перечисленных выше погрешностей в вероятностном ее выражении:

Выполним оценку каждого из слагаемых формулы (10.31) в зависимости от геометрии способа разбивки. При этом рассмотрим здесь только четыре основных способа разбивки, наиболее часто используемых при проведении указанных работ: способ прямой угловой засечки; способ обратной угловой засечки; способ линейной засечки; способ полярных координат.

Погрешности фиксации точки не зависят от геометрии способа разбивки, а определяются только технологической точностью закрепления точки на местности. Вынесенная точка может быть закреплена дюбелем в твердом покрытии, гвоздем на деревянной обноске, либо торце деревянного кола, накерниванием на металлических знаках или конструкциях сооружения и другими способами.

В способе прямой угловой засечки погрешность собственно разбивочных работ оценивается по одной из формул см. рис. 10.7:

Максимальная точность построения точки М в данном способе достигается при γ ≈ 109 ,50 .

291

Погрешность исходных данных определяется суммарной погрешностью в положении исходных пунктов А и В (mA; mB). Часто принимают значения mA = mB = mAB , исходя из равноточности построения геодезической основы в пределах локальной зоны, т.е. сравнительно близкого расположения данных исходных точек в общей системе построения опорной сети. Тогда, с учетом геометрии разбивки,

Принимая для приближенных расчетов s1=s2=s и γ = 90 0 , получим

По аналогичным формулам определяют и погрешность центрирования теодолита в точках А и В и используемых визирных целей, последовательно устанавливаемых в тех же точках:

где l – линейный элемент центрирования, определяемый несовпадением вертикальной оси вращения теодолита (визирной цели) с вершиной угла в соответствующей точке, либо с положением самой исходной точки (для визирных целей).

Если визирные цели не используются, т.е. наведение производится непосредственно на исходную точку, то

Часто для предварительных оценок принимают s1=s2=s. В этом случае при использовании визирных целей mЦ = l bs 2 , а при работе без визирных

целей - mЦ = l b s 2 .

В способе обратной угловой засечки (рис. 10.7) погрешность собственно разбивочных работ определяется по формуле

где mABC – погрешность построения пунктов геодезической разбивочной основы; t = (β1 + β2 + ω - 1800); S и b – средние значения сторон и базисов разбивки.

В способе линейной засечки (рис. 10.10) практически во всех случаях полагают, что точность ms отложения расстояний является одинаковой для s1 и s2 , что для симметричных построений при примерном равенстве этих расстояний вполне допустимо. В этом случае погрешность собственно разбивочных работ может быть оценена по формуле

292

а при γ = 90 0 mИСХ = mAB .

Если для построения расстояний используются оптические дальномеры, либо светодальномеры или электронные тахеометры, то обязательно необходимо учитывать в этом способе погрешность центрирования, которая здесь может быть оценена по формуле

а при γ = 90 0 mЦ = l .

В способе полярных координат (рис. 10.8) погрешность собственно разбивочных работ зависит от погрешности mβ построения угла и погрешности ms построения расстояния:

Из практического опыта известно, что погрешность построения угла (в линейной форме) меньше, чем погрешность построения расстояния, т.е.

принимая его значение, равным 2 – 3 единицам. С учетом (10.45) формулу (10.44) можно записать в виде

погрешностей центрирования оцениваются по практически идентичным формулам:

Из формул (10.47) и (10.48) следует, что для ослабления влияния погрешностей исходных данных и погрешностей центрирования отношение s/b должно быть минимальным, а угол β должен быть меньше прямого. Т.е. базис разбивки должен быть больше проектного расстояния.

293

При приближенных расчетах принимают β = 90о и s = b. Тогда

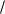2 и mЦ = l 2 .

Необходимая точность разбивочных работ определяется техническим заданием, и для исполнителя работ принятая точность построения проектных точек является безусловно обязательной. В связи с этим испонитель должен определить, какими приборами в том и другом способах разбивки он сможет обеспечить заданную точность построений непосредственно на местности. Рассмотрим решение указанной задачи для некоторых рассмотренных выше способов.

Значения точностных характеристик геодезических приборов входят как аргумент в формулы погрешностей собственно разбивочных работ (mPP). Выразим в формуле (10.31) значение mPP через другие погрешности, обозначив общую погрешность разбивки, определенную техническим заданием, через mТЗ:

С учетом формулы (10.32) для способа прямой угловой засечки можно записать условие выбора угломерного прибора для обеспечения заданной

причем погрешность исходных данных и погрешность центрирования предварительно вычисляются соответственно по формулам (10.35) и (10.37).

Из аналогичных преобразований для способа обратной угловой засечки получим

для способа линейной засечки без учета погрешности центрирования -

и с учетом погрешности центрирования -

В формулах (10.51) – (10.53) значения погрешностей исходных данных и погрешностей центрирования предварительно вычисляют по формулам, приведенным выше для указанных способов разбивки.

При оценках выбора технических средств для построения проектных точек способом полярных координат обычно сначала выбирают углоизмерительный прибор, точность которого должна удовлетворять условию:

Значения mИСХ и mЦ здесь определяют по формулам (10.47) и (10.49).

294