Из решения обратной геодезической задачи дирекционный угол αD3 = =208о05'04"; горизонтальное проложение dD3 = 18,552 м. Превышение h3-D =

=124,65 – 126,05 = -1,40 м.

Горизонтальный угол βD = αD3 - αDC = 208о05'04" – 153о29'05" = 54о35'59". Наклонное расстояние sD3 = 18,605 м.

Точка 4. Выносится на местность способом прямоугольных координат наклонными отрезками sСR (по линии СВ) и sR4 (по перпендикуляру к линии

СВ).

Горизонтальные проложения dСR и dR4 указанных отрезков найдем из

где αСВ = 224 о 20' 11"; αК4 = αСВ + 90о = 314 о 20' 11".

После подстановки в уравнения (10.22) всех известных величин получим

dCR = 15,092 м , dR4 = 9,041 м.

С топографического плана получим высоту точки R HR = 122,90 м. Следовательно, hR-C = -0,45 м , h4-R = +0,45 м.

Наклонные расстояния sСR = 15,099 м, sR4 = 9,052 м.

После выноса на местность точек 1, 2, 3 и 4 выполняют контрольные промеры расстояний 1-2, 2-3, 3-4 и 4-1 с определением соответствующих горизонтальных проложений и сравнивают полученные значения с проектными. Кроме того, в точках 1, 2, 3 и 4 измеряют теодолитом проектные горизонтальные углы (90о).

Точка М. Вынос точки на проектную высоту (123,45 м, табл. 10.3) осуществляется с точки С с контрольным определением ее значения с исходной точки D.

Вычисляют проектное превышение hМ-С(ПР)= НМ(ПР) – НС =123,450–123,357 =

=+ 0,093 м и контрольное проектное превышение hМ-D(ПР) = НМ(ПР) – НD = =123,450 – 126,050 = - 2,600 м.

Нивелир устанавливают посредине между точками С и М и выполняют построение проектной отметки в соответствии с правилами, изложенными в § 98.

Аналогичные работы выполняют и при контрольной проверке построения проектной высоты с точки D. Однако здесь следует иметь ввиду, что, скорее всего, с одной станции невозможно будет увидеть обе рейки, установленные в точках D и М, поскольку превышение между этими точками значительное, почти равно длине нивелирной рейки. В этом случае поверка построения высоты выполняется двумя станциями (ходом) через иксовую точку. Суммарное превышение (hx-D + hM-x) должно соответствовать проектному превышению hM-D(ПР).

§101. Разбивочные работы при трассировании

Вглаве 9 были рассмотрены вопросы нивелирования трассы, например, при строительстве дороги. Перед выполнением нивелирования производят

284

разбивку пикетажа, для чего используется теодолит и мерный прибор (дальномер, светодальномер, рулетка), либо только электронный тахеометр.

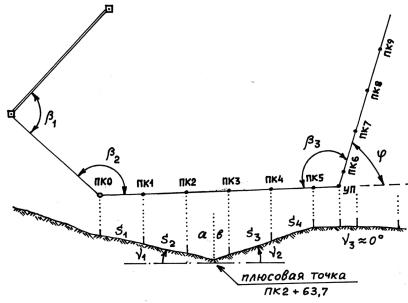
Для задания направления трассы от какого-либо исходного направления вычисляют проектное значение угла β и строят этот угол на местности, т.е. задают начальное направление трассы от пикета ПК) до первого угла ее поворота УП (рис. 10.15).

Рис. 10.15. Разбивочные работы при трассировании линейных сооружений.

Расстояние между пикетами соответствует 100 м в горизонтальном проложении (либо другому установленному расстоянию, например, 50 м). В связи с тем, что местность может иметь наклон к плоскости горизонта, в проектное расстояние вводят поправку за наклон. При перегибах местности между пикетами (например, между пикетами ПК2 и ПК3) поправки за наклон вводят для каждого из наклонных отрезков с учетом углов наклона ν1 и ν2.

По мере удаления трассы от пикета ПК) створ линии задают теодолитом, последовательно перемещая его на другие пикеты, с визированием на удаленный задний пикет отсчетом по горизонтальному кругу 0о. В этом случае продолжение створа будет соответствовать отсчету по горизонтальному кругу 180о.

В точке угла поворота УП выполняют разбивку кривой заданного радиуса. Основные элементы кривой вычисляют по формулам (9.25) – (9.29).

В процессе разбивки кривой все пикеты за углом поворота следует переместить вперед на величину домера (Д), поскольку длина кривой всегда меньше двух ее тангенсов (Т).

Детальная разбивка кривой может выполняться несколькими способами (рис. 10.16).

285

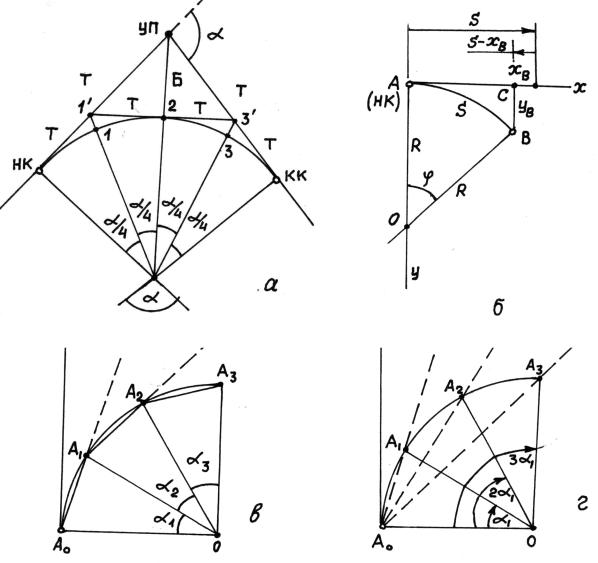
Рис. 10.16. Детальная разбивка кривых на трассе а) разбивка кривой по частям; б) способ координат; в) способ хорд; г) способ углов

При разбивке кривой по частям (рис. 10.16 а) всю ее, от начала кривой (НК) до конца кривой (КК), делят на две одинаковые кривые: НК-М и М-КК. Для каждой из них производят детальную разбивку, принимая значения НК1' = 1'2 = 23' = 3'КК = Т. При этом значение Т вычисляют по формуле

Точки 1' и 3' находятся на линиях НК-УП и КК-УП.

После построения точек 1' и 3' каждую из кривой разбивают способом координат (рис. 10.16 б).

В способе координат положение любой из точек кривой получают в условной системе прямоугольных координат хоy. Ось y – направление от начала кривой к ее центру 0; ось х – направление тангенса (Т), т.е. кассательной в точке начала кривой.

Координаты точки В, которая находится на расстоянии s, будут равны

286

где ϕ = Rs ρ ; ρ- радиан.

При радиусах до 500 м разбивку кривой ведут через 10 м, а при больших радиусах – через 20 м.

Технология разбивки следующая. От точки А рулеткой по направлению тангенса, задаваемому теодолитом, откладывают отрезок s. Находят разность (s – x) и откладывают ее в обратном направлении. В полученной точке устанавливают теодолит и строят им угол 90о от направления тангенса (линия СВ). Затем по направлению СВ откладывают координату у.

Схема разбивки кривых способом хорд (продолженных или последовательных) представлена на рис. 10.16 в).

При детальной разбивке кривой отрезки (хорды) АоА1 = А1А2 = А2А3 = а. Вообще говоря, значение а может быть и произвольным, но не более длины имеющейся рулетки. Для точки А1

Точки К1 и К2 и т.д. на кривой можно построить способом линейной засечки. По линии АоВо следует отложить хорду а до точки В1, а затем из нее отрезком 0,5s и из точки Ао отрезком а получить положение точки К1. В этом

случае s = aR2 .

Чтобы построить точку А2 продолжают линию АоА1 на расстояние а (А1А 2= а). Из точки А1 радиусом а и из точки А2' радиусом s засекают положение точки А2. Последующие точки получают аналогично.

При детальной разбивке способом углов (рис. 10.16 г) на кривой получают равноотстоящие друг от друга точки А1, А2, …, как и в способе хорд. Для этого в точке Ао устанавливают теодолит и ориентируют 0о горизонтального круга по направлению АоВо (по линии тангенса). Затем устанавливают по горизонтальному кругу отсчет 0,5α1 и в этом направлении откладывают хорду а (в точке А1). Далее снова по горизонтальному кругу устанавливают отсчет 2(0,5 α1), один конец рулетки фиксируют в точке А1, а другой ее конец на отсчете а совмещают в изображении через зрительную трубу теодолита с вертикальной нитью (точка А2) по команде наблюдателя. По аналогии с точкой А2 достраиваются остальные точки, изменяя каждый раз отсчет по горизонтальному кругу на 0,5α1. Такие же действия выполняют и из точки КК конца кривой.

Способ стягивающей хорды (рис. 10.17) используют обычно в тех случаях, когда радиус кривой слишком большой, а также в тех случаях, когда нет доступа к центру кривой и для построения переходных кривых.

287

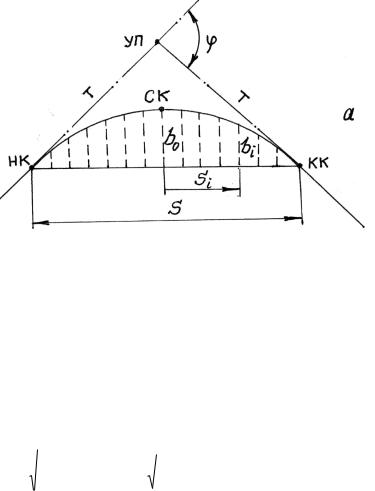
Рис. 10.17. Способ стягивающей хорды

При разбивке круговых кривых разбивочные работы выполняют по частям, короткими хордами, либо длинными хордами, но с учетом уклонения кривой от ходы. Если задаться значением угла φ , то можно определить длину хорды

а величину стрелки прогиба bo в середине кривой – по формуле

Величины стрелок прогиба bi получают по приближенной формуле:

через шаг в 2 м по обе стороны от стрелки bo. Поскольку круговая кривая симметричная, то величины рабочих промеров от середины кривой при равных шагах разбивки по обе стороны будут одинаковыми.

Переходные кривые выполняют в местах сопряжения круговых кривых с прямолинейными участками с целью ослабления резких ударов на поворотах при больших скоростях от действия центробежной силы. Для этого в местах сопряжений делают вставку (рис. 10.18), радиус которой изменяется от бесконечности (на прямой) до радиуса круговой кривой. После перехода через круговую кривую радиус изменяется соответственно от радиуса кривой до бесконечности.

Чаще всего для переходных кривых используют радиальную кривую (спираль), уравнение которой имеет вид

288