Глава 10 ГЕОДЕЗИЧЕСКИЕ РАЗБИВОЧНЫЕ РАБОТЫ

§95. Назначение и организация разбивочных работ

Врезультате выполнения разбивочных работ на местности находят с заданной или установленной точностью положение точек проектируемого сооружения.

Проектирование сооружения выполняют на топографическом плане, на нем же выполняют т.н. разбивочный чертеж с указанием значений основных разбивочных элементов, определяемых тем или иным способом построения точек, линий и т.п. элементов сооружения. Для перенесения на местность проекта сооружения используют особые его точки и линии: углы сооружения; главные, основные, промежуточные и детальные оси.

Для объектов линейного типа (траншеи, дороги, путепроводы и т.п.) главными осями являются их продольные оси, обычно оси симметрии. Основными осями для дорог являются оси, определяющие границы проезжей части, обочин, кюветов.

Рис. 10.1. Разбивочные оси сооружения.

Для зданий с симметричной геометрией главными осями являются оси симметрии (рис. 10.1). Так, для основного сооружения прямоугольной формы, определяемого точками Д1, А1, А7, Д7, главными осями являются оси Г-Г и 5-5. Основные оси определяют контур сооружения, т.е. определяют его форму и габариты (размеры). В соответствии с рис. 10.1 основными осями основного контура сооружения являются 1-1, 7-7, А-А, Д-Д, для пристройки – 2-2, 4-4, Д-Д (совпадающая с основной осью сооружения) и Е-Е. Промежуточные и детальные оси определяют положение различных

266

конструкционных элементов обычно внутри сооружения. К указанным осям относятся оси 3-3, 6-6, Б-Б и В-В, определяющие, например, расположение технологического оборудования. Обычно промежуточные и детальные оси выносят относительно главных и основных осей.

Указываемые в проекте сооружения или на разбивочном чертеже углы, координаты, расстояния, превышения, высоты называют проектными.

Высоты точек сооружения часто принимают условными. Например, для зданий за начальную (нулевую) отметку принимают уровень «чистого пола» первого этажа. В этом случае для подвальных помещений отметки будут отрицательными. Однако следует иметь ввиду, что при проектировании уровень «чистого пола» первого этажа задают в абсолютной отметке привязкой к местности, а затем принимают ее равной нулю для строительного чертежа.

Принцип производства разбивочных работ – от общего к частному. При разбивке главных и основных осей выполняется проектная ориентировка сооружения по сторонам света, а также его плановое расположение на местности относительно имеющейся ситуации. При детальной разбивке определяют положение отдельных элементов как относительно главных и основных осей, так и относительно друг друга.

Организация и технология разбивочных работ должна быть строго согласована с соответствующими этапами строительства объекта.

Для выполнения разбивочных работ на местности создают плановую и высотную геодезическую разбивочную основу, которая должна быть построена с заданной точностью определения ее координат и высот и закреплена на местности долговременными знаками в местах, обеспечивающих ее сохранность на весь период строительства.

Непосредственная разбивка сооружения на любом из этапов производится после соответствующей геодезической подготовки, в результате которой определяют разбивочные элементы (углы, расстояния, превышения и др.) для перенесения по ним на местность искомых точек и линий проекта. На первом этапе выполняют разбивку главных и основных осей, на втором этапе, после возведения фундаментов (выполнения «нулевого цикла»), от фактически закрепленных главных и основных осей разбивают продольные и поперечные оси отдельных частей сооружения. На третьем этапе, если этого требует назначение сооружения, выполняют разбивку технологических осей для установки оборудования.

Каждый из этапов разбивочных работ определяется различными требованиями точности. Например, если разбивка главных осей сооружения на местности может быть выполнена с погрешностью до 5 см, то детальные оси относительно главных часто разбивают на порядок точнее (до 3-5 мм). Во многих случаях установка технологического оборудования требует точности разбивки технологических осей до 1 мм и менее. В любом случае геодезическая основа должна обеспечивать необходимую точность разбивки. В связи с этим, при повышенных требованиях точности, создают дополнительную (обычно плановую) локальную геодезическую основу, которую закрепляют

267

уже внутри строящегося сооружения, привязываемую к фактическому положению главных осей.

Полевые разбивочные работы связаны, в основном, с построением на местности проектных горизонтальных углов, расстояний, превышений (высот) и уклонов.

§ 96. Построение на местности проектного горизонтального угла

Вынос на местность проектного горизонтального угла β с вершиной в точке 1 (рис. 10.2) выполняют при двух положениях вертикального круга: при «круге лево» (КЛ) и «круге право» (КП).

Рис. 10.2. Построение проектного угла

Теодолит устанавливают в рабочее положение в вершине проектного угла, выполняют наведение на опорную точку 2 и берут на нее отсчет 2(КЛ) по шкале горизонтального круга. В точке 2 при необходимости может быть установлена на штативе визирная цель с устройством для ее центрирования и горизонтирования. К полученному отсчету прибавляют (если угол откладывается по часовой стрелке) или отнимают от него (если угол откладывается против часовой стрелки) значение проектного угла βПР

и устанавливают полученный отсчет на шкале горизонтального круга сначала грубо, затем – точно наводящим винтом при закрепленной колонке. Положение направления на искомую точку А при «круге лево» по команде наблюдателя фиксируют шпилькой на местности. Меняют положение круга, берут отсчет 2(КП) на опорную точку 2, вычисляют отсчет на точку А

и устанавливают полученное значение на шкале горизонтального круга, как и в предыдущем случае. Положение направления на точку А при «круге право» фиксируют второй шпилькой на местности рядом с первой шпилькой. В случае расхождений в положении зафиксированных направлений за оконча-

268

тельное принимают среднее направление. Затем построенный угол измеряют теодолитом двумя-тремя полными приемами. Если расхождения в значениях измеренного и проектного углов соответствуют заданной точности построения, то задача считается выполненной. В противном случае необходимо заново построить угол.

В формулах (10.1) и (10.2) используют при отрицательных отсчетах и отсчетах, больших 3600.

Уточнение направления 1-А , соответствующее проектному углу, можно выполнить следующим способом.

Вычисляют значение

где d – расстояние от точки 1 до точки А (при построениях); ρ ′′ = 20626 5′′ . Полученное значение l откладывают в соответствующем направлении в точке А перпендикулярно к линии 1-А. Шпильку из точки А переносят в точку А' и для контроля двумя-тремя полными приемами измеряют построенный угол.

Вообще говоря, указанным способом можно строить проектные углы точнее, чем это позволяют возможности используемого теодолита. Например, при использовании теодолита Т30 проектный угол можно построить с точностью до 10".

откладывается в сторону уменьшения угла.

Новое измеренное значение построенного угла составило 73 036′22′′ , что является допустимым.

§ 97. Построение на местности проектного расстояния

Чаще всего приходится строить одновременно проектный угол и проектное расстояние s1A. В этом случае сначала выполняют построение проектного угла, размещая шпильки примерно на проектном расстоянии. После фикса-

269

ции на местности точки А' (рис. 10.2) точно измеряют расстояние линии 1-А' с учетом компарирования рулетки и поправок за наклон линии и вводят в

полученное расстояние поправку

Шпильку из точки А' переставляют по направлению линии 1-А' с учетом величины и знака поправки а.

Для контроля измеряют построенные проектный угол (в связи с подвижками проектной точки на местности могло произойти смещение с направления 1-А) и проектное расстояние. В том и другом случаях должна быть обеспечена заданная точность построения разбивочных элементов.

При использовании светодальномеров отражатель устанавливают по команде наблюдателя по створу линии 1-А до получения проектного расстояния (разбивочного элемента). При использовании электронных тахеометров одновременно фиксируют как значение проектного угла, так и значение проектного расстояния при перемещении в проектной точке

где ν - угол наклона проектной линии. Он может быть получен из отношения превышения h концов проектного отрезка к горизонтальному проложению d этого отрезка:

Поправка lH всегда положительная.

Если между номинальной и эталонной длиной l0 мерного прибора

Поправка lK отрицательная, если фактическая длина мерного прибора меньше номинальной, и положительная, если фактическая длина мерного прибора больше номинальной.

Поправка за температуру, как указывалось выше, зависит от коэффициента линейного расширения α материала, из которого изготовлена лента мерного прибора. Для стали принимают в расчетах α = 12∙10-6. Величина поправки за температуру

где t – рабочая температура; tK – температура компарирования мерного прибора. Поправка за температуру имеет знак «плюс», если рабочая температура меньше температуры компарирования. Если температура компарирования была меньше рабочей температуры, то поправка за температуру принимается отрицательной.

Таким образом, фактическая проектная длина на местности с учетом поправок определяется по формуле

270

Пример 10.2. Построение проектного расстояния.

Получено проектное значение горизонтального проложения dПР = 69,738 м, которое необходимо построить с относительной погрешностью δ не более 1:10000. Превышение концов проектной линии h = 0,805 м. Для построения на местности используется стальная рулетка Р100 (номинальная длина 100 м), при компарировании которой при температуре tK = 180С получена эталонная ее длина 100,0035 м. Рабочая температура при построении линии составила t = 220С.

Решение.

Абсолютная погрешность построения проектного расстояния составляет

Обратите внимание на то, что при указанных в примере условиях поправки практически компенсировали друг друга, а фактический отсчет по рулетке, соответствующий проектному (расчетному) расстоянию, оказался даже несколько меньше проектного значения горизонтального проложения. Это оказалось следствием сравнительно малого угла наклона проектной линии. Чаще всего на пересеченной местности поправки за наклон линии значительно превышают остальные.

При контрольном измерении построенного расстояния той же рулеткой и при той же рабочей температуре измеренная длина оказалась равной 69,741 м. Разность с проектной длиной составила (69,741 – 69,737) = +0,004 м = +4 мм, что меньше допустимой величины погрешности построения (7 мм – см. исходные данные примера и начало решения).

§98. Построение на местности проектных отметок

илиний заданного уклона

Часто от репера Государственной нивелирной сети невозможно передать высоту непосредственно на проектную точку. Для этого, как отмечалось выше, создают высотную геодезическую основу, которую закрепляют на строительной площадке. Саму высотную основу привязывают нивелирным ходом, либо системами нивелирных ходов к исходным пунктам (реперам) геодезической сети.

Для выноса на местность проектной отметки используют, в основном, метод геометрического нивелирования, реже, при невозможности использовать указанный выше метод, - метод тригонометрического нивелирования.

Для выноса проектной отметки методом геометрического нивелирования нивелир устанавливают посредине между исходной и проектной точками

271

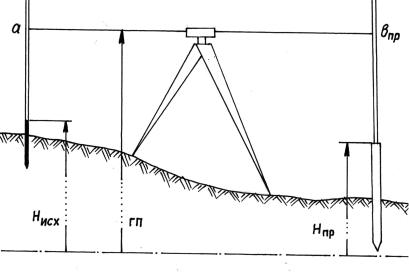
где а – отсчет по рейке, установленной на исходной точке.

Формулу (10.11) удобно использовать, если с данной станции выносят сразу несколько проектных высот.

Рис.10.3. Построение проектной отметки способом геометрического нивелирования

Поскольку проектная высота НПР известна, то известно и проектное превышение

где bПР – отсчет по рейке, установленной в проектной точке, соответствующий проектной высоте. Таким образом,

Высотное положение проектной точки изменяют до тех пор, пока на рейке не установится отсчет, равный bПР. После этого превышение hПР измеряют несколько раз (при нескольких горизонтах прибора) и убеждаются в обеспечении заданной точности построения высоты.

Проектная точка может быть подвижной по высоте, выполненной в виде болта (в конструкции), ею может быть деревянный или металлический кол, забиваемый в землю, часто на строительных конструкциях проектной точкой является черта (откраска) по основанию рейки.

При строительстве зданий всегда требуется передача проектной высоты (отметки) на другой монтажный горизонт, например, по колонне или стене. Для этого от проектной черты на стене или колонне нижнего горизонта рулеткой откладывают проектную разность двух монтажных горизонтов. При передаче высот на несколько монтажных горизонтов на каждом из них выполняют контрольное нивелирование по проектным отметкам.

При использовании для построения проектной отметки метода тригонометрического нивелирования в исходной точке (в точке с известной высотой) устанавливают теодолит (рис. 10.4), измеряют его высоту i, горизонтальное проложение d и определяют угол наклона ν, соответствующий проектной высоте НПР:

272

Рис.10.4. Построение проектной отметки способом тригонометрического нивелирования

Определяют отсчет по вертикальному кругу теодолита при «круге право» и «круге лево», соответствующие значению полученного проектного угла наклона:

где МО – место нуля, предварительно определенное на станции по 2-3 точкам.

Метка М будет соответствовать проектной высоте в заданной точке.

Для контроля построения проектной отметки следует изменить горизонт прибора, измерить несколькими приемами угол наклона на метку М и вычислить значение проектной высоты по формуле:

Если при построении не будет обеспечена заданная точность, то метку М перемещают на величину расхождения в соответствующем направлении и выполняют контрольную проверку высоты.

Построение линии с проектным уклоном можно выполнить с помощью нивелира, либо с помощью теодолита.

Геометрическое нивелирование удобно использовать при небольших проектных уклонах, например, при строительстве дорог. При значительных уклонах используют теодолит.

На рис. 10.5 представлена схема построения линии. Нивелир устанавливают в створе проектной линии в точке 1 (рис. 10.5 а), высота которой

известна (Н1(ПР)). Далее, на расстояниях di от точки 1, выставляют точки на их проектную высоту

273

с вычислением для каждой из них соответствующего отсчета по рейке, как это выполнялось при передаче на точку проектной высоты.

Рис. 10.5. Построение линии заданного уклона а) горизонтальным лучом; б) наклонным лучом нивелира; в) с помощью теодолита

В другой схеме (рис. 10.5 б) определяют проектную высоту в конечной точке 2 линии и элевационным винтом нивелира добиваются совпадения отсчетов а по рейкам, установленным в точках 1 и 2. Далее, в промежуточных точках по створу линии выставляют точки, на которых отсчет по рейке также должен быть равным отсчету а.

Во второй схеме вместо нивелира можно использовать теодолит (рис. 10.5 в). Теодолит устанавливают в проектной точке 1, определяют проектный угол наклона

по нескольким измерениям определяют место нуля вертикального круга и вычисляют по формулам (10.15) отсчет по вертикальному кругу, соответствующий проектному углу. При полученном отсчете визируют на точку 2 проектной линии и по рейке, установленной в этой точке, берут отсчет а. Для промежуточных точек линии должны также обеспечиваться такие же отсчеты по рейкам.

274

После построения линии с заданным уклоном необходимо выполнить контрольные измерения по ее зафиксированным на местности точкам и убедиться в правильности построения, т.е. в обеспечении необходимой точности построения проектного уклона. Целесообразно контрольные измерения выполнять способом геометрического нивелирования, если это возможно по условиям измерений.

Пример 10.3. Построение проектного уклона с помощью теодолита. Исходные данные.

Величина проектного уклона iПР =-0,145. Точность построения уклона ± 0,005 . Место нуля МО = -0002,4'. Горизонтальное проложение линии 1-2 d12 = 65,356 м.

Проектная вы-сота в точке 1 Н1(ПР) = 156,857 м.

Решение.

Определяем проектную высоту в точке 2:

Н2(ПР) = Н1(ПР) + d12iПР = 156,857 + 65,356(-0,145) = 147,380 м.

По формулам (10.18) и (10.15) находим значения проектного угла и отсчетов по вертикальному кругу при «круге лево» и «круге право»: νПР = -8015,0'; ВК(КЛ) = -8015,0' + +(- 0002,4') = -8017,4'; ВК(КП) = -0002,4'- (-8015,0') = +8012,6'.

Отсчет по рейке в точке 2 при наблюдениях после установки отсчетов по вертикальному кругу при положениях КЛ и КП составил а2 = 1476 мм.

При контрольном нивелировании максимальное расхождение в проектных высотах по линии 1-2 на расстояниях 15 м составило 15 мм. Таким образом, ошибка в построении проектного уклона составила 15 мм/15000 мм = 0,001, что удовлетворяет поставленной задаче.

При выполнении аналогичных работ, не требующих высокой точности, можно пользоваться тремя визирками одинаковой длины (рис. 10.6), которые представляют собой вертикальный брусок с прикрепленной к нему горизонтальной планкой.

Рис. 10.6. Построение проектного уклона с помощью визирок.

Две визирки устанавливают в точках 1 и 2 с предварительно выставленными на них проектными отметками. Третью визирку перемещают по створу линии 1-2 и «на глаз» совмещают горизонтальные планки всех трех визирок (наблюдатель должен находиться в точках 1 или 2. По основанию третьей визирки фиксируют точку с ее проектной высотой, соответствующей заданному проектному уклону.

275