делать», обычно в них приводятся указания «что делать». Вот здесь большую помощь Вам и может оказать своя библиотечка: справочники, учебная литература, методические указания, а также и Ваши записи (хотя бы на первых порах) на лекциях и практических занятиях по специальным дисциплинам.

В списке рекомендуемой литературы, приведенном в конце учебника, указана лишь небольшая часть изданий разных лет по различным направлениям инженерной геодезии, топографии и др., а также маркшейдерскому делу. Некоторые из них имеются в библиотеке вуза, другую литературу аналогичного содержания можно найти в букинистических магазинах.

Глава 2. ТОПОГРАФИЧЕСКИЕ КАРТЫ И ПЛАНЫ

§ 6. Влияние кривизны Земли на измеренные расстояния

При выполнении геодезических работ на сравнительно небольших территориях поверхность Земли можно принимать за плоскую, и измеренные расстояния на плоском изображении принимать равными соответствующим расстояниям на сферической поверхности. При измерениях значительных по величине расстояний необходимо учитывать влияние кривизны поверхности Земли.

Для простоты изложения примем, что Земля представляет собой шар радиусом R (радиус Земли, представляемой в виде шара, принимают равным 6371,11 км). Предположим, что по поверхности шара из точки А в точку В перемещается материальная точка (рис. 2.1), при этом расстояние S = АВ , которое пройдет эта точка по поверхности шара, равно

, (2.1) где α - центральный угол дуги АВ (в радианах).

15

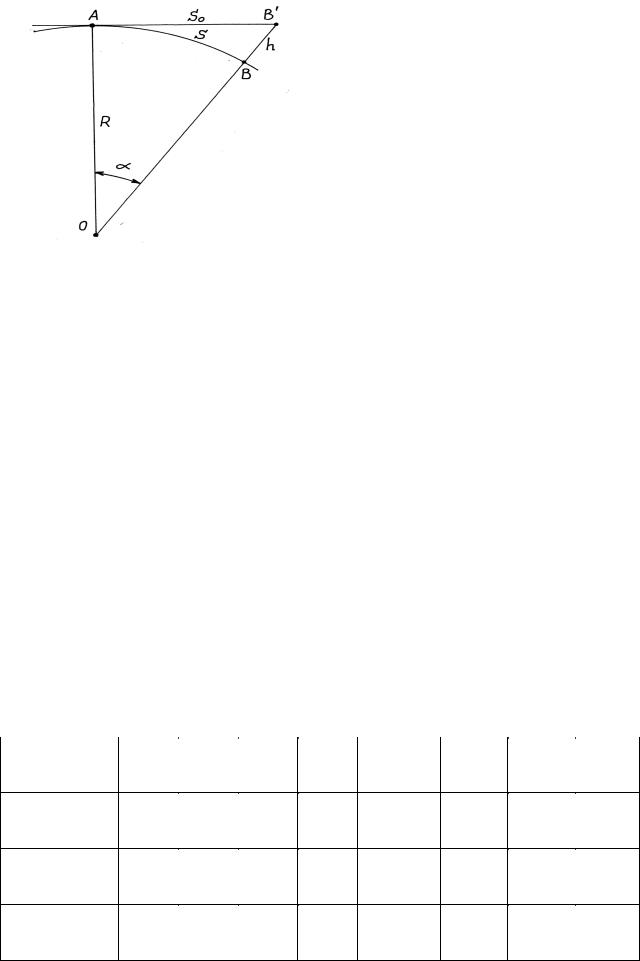
Предположим, что точка движется по касательной в точке А к поверхности шара и пройдет по нему путь Sо = AB', соответствующий движению по поверхности шара на пути S. Для величины So можно записать:

поскольку α = S / R.

Аналогично рассмотрим влияние кривизны Земли на определение

Оценка возможных погрешностей при измерениях вертикальных и горизонтальных расстояний приведена в табл. 2.1.

Таблица 2.1

16

Точность измерения линий в геодезических сетях высших классов определяется относительной погрешностью порядка 1:400000, что практически является соизмеримым для S = 10 км (и, конечно, более 10 км). До 10 км при измерении горизонтальных расстояний во многих случаях влиянием кривизны Земли можно пренебречь.

Совсем другая картина наблюдается при оценке погрешностей в вертикальных отрезках. Точность определения высот при геодезических работах, например, при топографической съемке, определяется величиной 5 см, т.е. уже для расстояний S = 1000 м необходимо учитывать кривизну Земли. Если же точность измерений выше, например 5 мм, то учет кривизны Земли следует начинать примерно для расстояний S = (250 – 300) м, что легко проверить обратным расчетом по формуле (2.6).

§ 7. Краткие сведения о картографических проекциях

Картографическое изображение – это представление исходной информации об объектах, а также о явлениях действительности, в графической, цифровой или другой форме на заданной поверхности (носителе информации) с применением системы специальных картографических условных знаков.

Очевидно, что на картах невозможно отобразить все детали объектов или явлений, поэтому на них показывают только типичные отличительные свойства в обобщенном виде с указанием связей, которые позволяют облегчить чтение карты и решение с помощью нее поставленных задач.

Картографическая проекция – это установленный способ изображения поверхности земного эллипсоида (референц-эллипсоида) на плоскости. Поверхность эллипсоида (шара, сфероида и т.п.) невозможно развернуть на плоскость без деформаций, в связи с чем при переходе на плоскость возникает сжатие или растяжение изображения, т.е. изменение его масштаба.

Под масштабом карты понимается отношение длины отрезка на изображении к длине соответствующего отрезка на местности, выраженном в тех же единицах измерения. Масштаб карты указывают в численном виде (1: 5 000; 1: 200 000 и т.п.) или именованном виде (в 1 см 250 м, т.е. в 1 см 25 000 см, или масштаб 1: 25 000).

Картографические проекции классифицируют по двум признакам: по характеру искажений углов (равноугольные) и площадей (равновеликие) и по виду координатной сетки параллелей и меридианов (азимутальные, конические, цилиндрические и др.).

Меридианом (рис. 1.4) является линия пересечения с поверхностью Земли плоскости, проходящей через ось РР вращения Земли. Меридиан, проходящий через определенную точку в Гринвичской обсерватории (Англия), называется Гринвичским (нулевым, начальным) меридианом.

17

Параллель получается от пересечения с поверхностью Земли плоскости, перпендикулярной к оси вращения Земли. Самая большая параллель называется экватором.

Равноугольные проекции передают без искажений углы геометрических фигур, а равновеликие не искажают площадей. Кроме того, существуют и произвольные проекции, которые не являются равновеликими или равноугольными, а используются для построения изображений в удобной для представления и чтения форме.

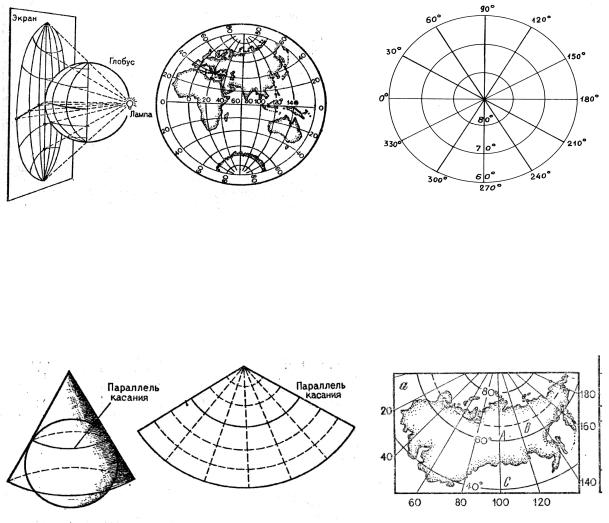
Азимутальные проекции (рис. 2.2) часто используются для изображения полярных областей. В нормальных азимутальных проекциях меридианы изображаются прямыми линиями, исходящими из точки северного или южного полюса, а параллели являются концентрическими окружностями, центром которых является точка полюса.

Рис.2.2. Азимутальная проекция.

Конические проекции (рис.2.3) получаются при проектировании поверхности эллипсоида на коническую поверхность, которая потом разворачивается в плоскость. Меридианы нормальных конических поверхностей являются прямыми линиями, а параллели – окружностями.

Рис. 2.3. Коническая проекция.

Как азимутальные, так и конические проекции, кроме нормальных могут быть поперечными и косыми. В этих случаях меридианы и параллели на них изображаются сложными кривыми.

18

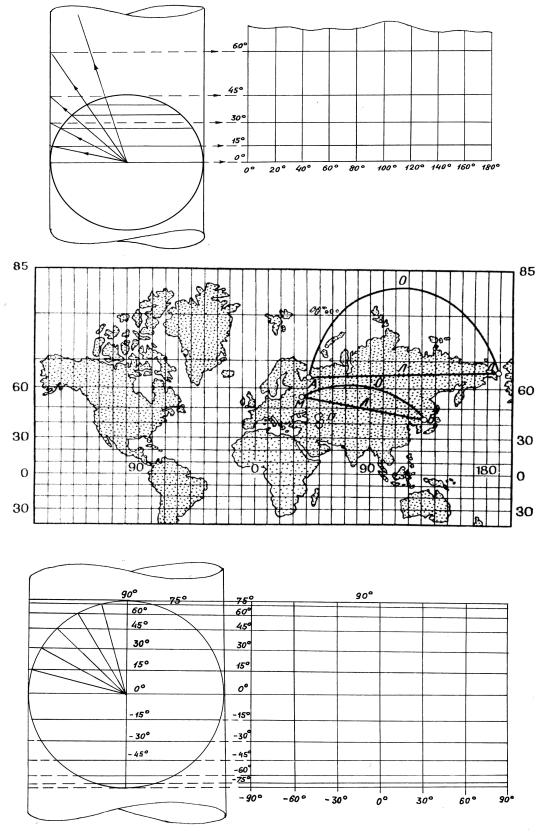
Рис. 2.4. Проекция Меркатора.

Рис.2.5. Проекция Ламберта.

Из цилиндрических проекций наиболее распространенными являются

проекция Меркатора, изображенная на рис.2.4, проекция Ламберта (рис.2.5) и проекция Гаусса (1777 – 1855 гг.) – рис 2.7.

19