
- •Предисловие
- •Глава 1. Вводная часть
- •§ 1. Предмет и задачи геодезии
- •§ 2. Краткие исторические сведения
- •§ 3. Единицы измерений, применяемые в геодезии
- •§ 4. Фигура и размеры Земли
- •§ 5. Содержание курса и рекомендации по его изучению
- •Глава 2. Топографические карты и планы
- •§ 6. Влияние кривизны Земли на измеренные расстояния
- •§ 7. Краткие сведения о картографических проекциях
- •§ 8. Общие сведения о топографических картах и планах
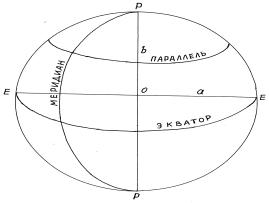
- •§ 9. Система географических координат
- •§ 10. Равноугольная поперечно-цилиндрическая проекция Гаусса-Крюгера
- •§ 11. Разграфка и номенклатура топографических карт и планов
- •§ 12. Зональная система плоских прямоугольных координат Гаусса
- •§ 13. Перевычисление координат из зоны в зону
- •§ 14. Система высот
- •§ 15. Условные знаки топографических карт и планов
- •§ 16. Изображение рельефа на топографических картах и планах
- •§ 17. Ориентирование
- •§ 18. Решение некоторых задач с использованием топографической карты
- •18.1. Измерение расстояний
- •18.2. Определение географических и прямоугольных координат
- •18.3. Ориентирование линий
- •18.4. Ориентирование карты на местности
- •18.5. Определение высот точек
- •18.6. Построение профиля
- •18.7. Построение линии заданного уклона
- •18.9. Определение площадей на топографических картах и планах
- •§ 19. Виды измерений
- •§ 20. Классификация погрешностей измерений
- •§ 21. Свойства случайных погрешностей
- •§ 22. Среднее арифметическое
- •§ 23. Средняя квадратическая погрешность
- •§ 24. Средние квадратические погрешности функций измеренных величин
- •§ 25. Обработка ряда равноточных измерений одной величины
- •§ 26. Об учете систематических погрешностей в измерениях
- •§ 27. Средняя квадратическая погрешность двойных равноточных однородных измерений
- •§ 28. Понятие о весе результата измерения
- •§ 29. Средняя квадратическая погрешность единицы веса и арифметической середины
- •§ 30. Обработка ряда неравноточных измерений одной величины
- •Глава 4. Государственные геодезические сети
- •§ 31. Назначение Государственных геодезических сетей
- •§ 32. Классы геодезических сетей
- •§ 33. Методы построения Государственных геодезических сетей
- •§ 34. Закрепление пунктов геодезических сетей
- •§ 35. Оценка точности построения опорных геодезических сетей
- •§ 36. Оценка точности построения сетей триангуляции
- •§ 37. Оценка точности построения звена полигонометрии
- •§ 38. Оценка точности построения сетей трилатерации
- •Глава 5. Геодезические приборы
- •§ 39. Классификация геодезических приборов
- •§ 40. Теодолиты
- •§ 41. Зрительные трубы
- •§ 42. Уровни и компенсаторы наклона
- •§ 43. Устройство теодолита
- •§ 44. Установка теодолита в рабочее положение
- •§ 45. Измерение горизонтальных углов и углов наклона
- •45.1. Способ приемов
- •45.2. Способ повторений
- •45.3. Способ круговых приемов
- •45.4. Измерение углов наклона
- •§ 46. Поверки теодолитов
- •§ 47. Нивелиры
- •§ 48. Устройство нивелира
- •§ 49. Нивелирные рейки
- •§ 50. Установка нивелира в рабочее положение
- •§ 51. Измерение превышений
- •§ 52. Поверки нивелиров
- •§ 53. Приборы для линейных измерений
- •§ 54. Гироскопические приборы
- •§ 55. Приборы для поиска подземных коммуникаций
- •Глава 6. Оптико-электронные геодезические приборы
- •§ 56. Общие замечания
- •§ 57. Краткие сведения о лазерных источниках излучения
- •§ 58. Электромагнитные дальномеры
- •§ 59. Светодальномеры
- •§ 60. Интерферометры
- •§ 61. Угломерные приборы
- •§ 62. Электронные тахеометры
- •§ 63. Электронные нивелиры
- •§ 64. Лазерные приборы
- •Глава 7. Построение съемочного обоснования
- •§ 65. Назначение и виды теодолитных ходов
- •§ 66. Прямая и обратная геодезические задачи на плоскости
- •§ 67. Взаимосвязь дирекционных углов с измеренными на местности горизонтальными углами
- •§ 68. Привязка теодолитных ходов
- •68.1. Способ примыкания
- •68.2. Прямая угловая засечка
- •68.3. Линейная засечка
- •68.4. Обратная угловая засечка
- •68.5. Комбинированные засечки
- •68.6. Задача П.А.Ганзена
- •§ 69. Особые системы теодолитных ходов
- •§ 70. Снесение координат с вершины знака на землю
- •§ 71. Определение элементов приведения и редукции
- •§ 72. Привязка теодолитных ходов к стенным геодезическим знакам
- •§ 73. Спутниковые методы определения координат
- •§ 74. Организация полевых работ при построении съемочного обоснования
- •74.1. Рекогносцировка и закрепление точек съемочного обоснования
- •74.2. Подготовка абрисов горизонтальной съемки
- •74.3. Поверки теодолита и нивелира
- •74.4. Компарирование мерных приборов
- •74.5. Измерение длин линий
- •74.6. Измерение горизонтальных углов и углов наклона
- •§ 75. Вычисления в разомкнутом теодолитном ходе
- •75.1. Предварительные вычисления
- •75.2. Обработка результатов угловых измерений
- •75.3. Вычисление приращений координат и оценка точности хода
- •75.4. Рекомендации к поиску вероятных погрешностей в измерениях и вычислениях при обработке ведомости координат
- •75.5. Уравнивание приращений координат и вычисление координат точек хода
- •75.6. Обработка ведомости высот
- •§ 76. Вычисления в замкнутом теодолитном ходе
- •76.1. Оценка точности угловых измерений и вычисление дирекционных углов
- •76.2. Вычисление приращений координат и оценка точности хода
- •76.3. Уравнивание приращений координат и вычисление координат точек хода
- •76.4. Обработка ведомости высот
- •§ 77. Обработка диагонального хода
- •Глава 8. Топографические съемки
- •§ 78. Назначение и виды топографических съемок
- •§ 79. Понятие о цифровой модели местности
- •§ 80. Теодолитная съемка
- •§ 81. Тахеометрическая съемка
- •§ 82. Составление плана местности по результатам топографической съемки
- •82.2. Нанесение на план точек съемочного обоснования
- •82.3. Нанесение на план результатов тахеометрической съемки
- •82.4. Рисовка рельефа и ситуации
- •82.5. Построение на плане ситуации по результатам теодолитной съемки
- •Глава 9. Нивелирные работы
- •§ 83. Способы и методы нивелирования
- •§ 84. Способы геометрического нивелирования
- •§ 85. Основные источники погрешностей геометрического нивелирования
- •§ 86. Техническое нивелирование
- •§ 87. Трассирование
- •§ 88. Расчет и разбивка главных точек кривых на трассе
- •§ 89. Нивелирование поперечных профилей
- •§ 90. Обработка результатов нивелирования трассы
- •§ 91. Построение профиля трассы
- •§ 92. Построение проектной линии
- •§ 93. Построение поперечного профиля и проектного полотна дороги
- •§ 94. Нивелирование площадей
- •Глава 10. Геодезические разбивочные работы
- •§ 95. Назначение и организация разбивочных работ
- •§ 96. Построение на местности проектного горизонтального угла
- •§ 97. Построение на местности проектного расстояния
- •§ 99. Способы разбивочных работ
- •§ 100. Расчет разбивочных элементов
- •§ 101. Разбивочные работы при трассировании
- •§ 102. Разбивка фундаментов инженерных сооружений
- •§ 103. Оценка точности разбивочных работ
- •Глава 11. Геодезические работы в строительстве
- •§ 104. Общие положения
- •§ 105. Краткие сведения об объектах строительства
- •§ 106. Геодезические работы при строительстве промышленных сооружений
- •§ 107. Геодезические работы при строительстве гражданских зданий
- •§ 108. Геодезические работы при строительстве дорог и мостовых сооружений
- •§ 109. Геодезические работы при планировании и застройке населенных пунктов
- •§ 110. Геодезические работы при строительстве подземных коммуникаций
- •§ 111. Геодезические работы при строительстве гидротехнических сооружений
- •Глава 12. Геодезические работы в подземном строительстве
- •§ 115. Горизонтальная соединительная съемка
- •115.2. Горизонтальная соединительная съемка через один шахтный ствол
- •§ 116. Вертикальная соединительная съемка
- •§ 117. Подземная горизонтальная съемка
- •§ 118. Подземная вертикальная съемка
- •§ 119. Геодезические разбивочные работы в подземном строительстве
- •§ 120. Задачи и содержание топографо-геодезических работ
- •§ 121. Точность геодезических работ
- •§ 122. Создание топографических карт и планов
- •§ 123. Разбивка геодезических сеток и профильных линий
- •§ 124. Разбивочные работы при проведении геологической разведки
- •§ 126. Виды деформаций инженерных сооружений
- •§ 127. Задачи наблюдений и организация работ
- •§ 128. Геодезические знаки и их конструкции
- •§ 129. Размещение геодезических знаков на инженерных сооружениях
- •§ 130. Точность измерения деформаций
- •§ 131. Периодичность наблюдений
- •§ 132. Наблюдения за вертикальными перемещениями
- •§ 133. Наблюдения за горизонтальными смещениями
- •§ 134. Наблюдения за кренами
- •§ 135. Наблюдения за деформациями земной поверхности
- •§ 136. Разработка методики наблюдений
- •§ 137. Обработка и анализ результатов наблюдений
- •Глава 15. Особенности точных и высокоточных измерений
- •§ 138. Основные группы погрешностей измерений
- •§ 139. Учет влияния рефракции атмосферы
- •§ 140. Высокоточное и точное геометрическое нивелирование
- •§ 141. Нивелирование I класса
- •§ 142. Нивелирование II класса
- •§ 143. Нивелирование III и IV классов
- •§ 144. Особенности точного и высокоточного нивелирования при наблюдениях за деформациями
- •§ 145. Высокоточные и точные угловые измерения
- •§ 146. Высокоточные и точные измерения в схемах микротриангуляции, микротрилатерации и короткобазисной полигонометрии
- •Глава 16. Уравнивание геодезических построений
- •§ 147. Основные задачи уравнительных вычислений
- •§ 148. Метод наименьших квадратов
- •§ 149. Классификация основных способов уравнивания
- •§ 150. Основные геометрические условия, возникающие в построениях
- •150.1. Условие фигуры
- •150.2. Условие горизонта
- •150.3. Условие суммы углов
- •150.4. Условие дирекционных углов
- •150.5. Условие сторон
- •150.6. Условие полюса
- •150.7. Условие координат
- •§ 151. Методы решения систем линейных нормальных уравнений
- •151.1. Способ последовательной подстановки
- •151.2. Способ матричных преобразований
- •151.3. Решение систем линейных уравнений по алгоритму Гаусса
- •151.4. Способ краковянов
- •§ 152. Коррелатный способ уравнивания
- •§ 153. Примеры коррелатного способа уравнивания
- •153.1. Уравнивание углов в полигоне
- •153.2. Уравнивание системы нивелирных ходов с несколькими узловыми точками
- •153.3. Уравнивание полигонометрического хода
- •153.4. Уравнивание системы полигонометрических ходов с двумя узловыми точками
- •153.5. Уравнивание триангуляции
- •153.6. Уравнивание триангуляции по условию координат
- •§ 154. Параметрический способ уравнивания
- •§ 155. Примеры параметрического способа уравнивания
- •155.1. Уравнивание углов в полигоне
- •155.2. Уравнивание системы нивелирных ходов с несколькими узловыми точками
- •155.3. Уравнивание полигонометрического хода
- •155.4. Уравнивание системы полигонометрических ходов с двумя узловыми точками
- •155.5. Уравнивание направлений в триангуляции
- •§ 156. Способ раздельного уравнивания
- •156.1. Уравнивание полигонометрического хода
- •156.2. Система полигонометрических ходов с одной узловой точкой
- •156.3. Система нивелирных ходов с одной узловой точкой
- •§ 157. Способ эквивалентной замены
- •§ 158. Способ полигонов В.В.Попова
- •§ 159. Способ последовательных приближений
- •§ 160. Оценка точности уравненных элементов и их функций
- •160.1. Общие положения
- •160.2. Оценка точности при уравнивании коррелатным способом
- •160.3. Оценка точности при уравнивании параметрическим способом
- •Предметный указатель
- •Список литературы
- •Оглавление
мн.др. разработаны методы и приборы для обработки фотографической информации с целью получения карт и планов местности.
§ 3. Единицы измерений, применяемые в геодезии
Измеряемые при геодезических работах величины выражаются в метрической и угловой системах счета.
Единицей линейных расстояний является метр и производные от него (километр, сантиметр, миллиметр): 1 км = 1000 м; 1 м = 100 см = 1000 мм.
Для определения площадей основной единицей измерения является квадратный метр и производная от него единица – квадратный километр: 1 км² = 1000000 м² , а также гектар: 1 га = 10000 м² = 0,01 км² .
Единицей измерения углов, направлений является градус, дробными частями которого являются минуты и секунды: 1°= 60´= 3600″. Часто в качестве угловой меры используют радиан, равный (180/π) градусам, т.е. 1 рад = 57,29577951° = 3437,746770´ = 206264,8062″, а 1° = 0,017453293 рад.
Во многих приборах используется единица десятичной меры углов, которая равна 1/100 прямого угла – град. Град делится на 100 градовых минут, а каждая градовая минута – на 100 градовых секунд. Таким образом, 1 град = 0,9о = 54' = 3240".
§ 4. Фигура и размеры Земли
«В природе все должно быть гармонично и совершенно. Земля должна быть тоже совершенна. Но совершеннейшим из геометрических тел является шар. Значит, Земля – шар». Это первая зафиксированная гипотеза шарообразности Земли, была высказана известным древнегреческим ученым Пифагором (580 – 500 гг.). Сомнительная даже с точки зрения логики гипотеза оказалась во многом правильной.
Шарообразность Земли была установлена, как отмечалось выше, Эратосфеном примерно 2230 лет назад, однако такие же предположения были и у халдейских жрецов, изучавших движение Луны, Солнца, звезд и планет солнечной системы.
С открытием Д.Кассилем (1625 – 1712 гг.) полярного сжатия Юпитера и доказательствами И.Ньютона (1642 – 1727 гг.) о форме вращающегося в пространстве жидкого тела (форма сфероида или эллипсоида вращения) началось детальное изучение формы Земли.
10
Очевидно, что шар и сфероид представляют собой математические фигуры с гладкими кривыми поверхностями (рис. 1.4), форма и
|
размеры которых однозначно опреде- |
||
|
ляются по их основным параметрам: |
||
|
для шара – это радиус R, для сферо- |
||
|
ида – это размер одной из его полуо- |
||
|
сей (большой - |
а или малой – b) и |
|
Рис. 1.4. Сфероид. |
полярное сжатие α, определяемое |
||
как отношение |
(а – b)/а. |
||
|
|||
В действительности физическая поверхность Земли имеет весьма сложную форму, которую невозможно описать простыми математическими зависимостями. Под физической поверхностью Земли понимается поверхность суши и невозмущенная поверхность всех внешних морей и океанов. Известно, что распределение масс (плотностей) в теле Земли весьма неравномерно. Это приводит к тому, что направления отвесных линий, если форму Земли в первом приближении принять за сфероид, не будут совпадать с направлениями нормалей к поверхности сфероида. В результате образуется поверхность весьма сложной формы (уровенная поверхность), в каждой точке которой линия направления силы тяжести совпадает с нормалью к этой же поверхности. По предложению в 1873 г. немецкого физика Листинга (1808 – 1882 гг.) тело, ограниченное такой поверхностью, названо геоидом (землеподобным).
Геоид близок к сфероиду, но в общем случае не совпадает с ним. Отступления поверхности геоида от поверхности сфероида в некоторых местах Земли достигают ±(100 – 150) м. На акватории мирового океана форма геоида с помощью спутниковых наблюдений определяется весьма точно, с погрешностями порядка 0,1 – 0,3 м. На суше погрешность определения формы геоида уже значительна, порядка 1,5 – 2,0 м. В связи с этим для суши принята вспомогательная поверхность, положение которой определяется весьма точно. Эта поверхность называется поверхностью квазигеоида, а тело, ограниченное этой поверхностью, называют квазигеоидом.
Таким образом, зная форму геоида (квазигеоида), можно подобрать форму Земли (общий земной эллипсоид – ОЗЭ), определяемую простыми для использования математическими зависимостями, для которой выполнялись бы следующие условия:
-центр ОЗЭ совпадает с центром масс Земли;
-малая полуось совпадает с осью вращения Земли;
-объем ОЗЭ равен объему геоида (квазигеоида);
-сумма квадратов отклонений поверхности ОЗЭ от поверхности геоида (квазигеоида) в целом для всей Земли должна быть минимальной.
Для практических целей физическую поверхность Земли проектируют на вспомогательную поверхность, имеющую простую форму. Эта поверхность называется поверхностью относимости. Поверхность относимости должна
11

незначительно отличаться от поверхности квазигеоида в пределах какойлибо территории, например, Европы, Азии, либо отдельного государства. В масштабах всей Земли удобно использовать общий земной эллипсоид, а в масштабах ограниченной территории за поверхность относимости удобно принимать другой эллипсоид (референц-эллипсоид), ориентировка которого в теле Земли может отличаться от ориентировки ОЗЭ, при этом малая ось референц-эллипсоида может и не совпадать с осью вращения Земли, а быть ей параллельной. В табл. 1.1 приведена историческая справка по определению параметров земного эллипсоида (референц-эллипсоидов).
До настоящего времени используются различные референц-эллипсоиды: в Германии – эллипсоид Бесселя (1841 г.), в Великобритании – эллипсоид Кларка (1880 г.), в США – эллипсоид Хейфорда (1909 г.). В России до 1942 г. использовался эллипсоид Бесселя. При детальном исследовании этого референц-эллипсоида оказалось, что он дает весьма большие погрешности в положении точек на поверхности Земли в пределах России. Под руководством русского ученого Ф.Н.Красовского (1878 – 1948 гг.) выполнены расчеты по определению параметров референц-эллипсоида для России. С 1946 г. параметры полученного референц-эллипсоида приняты для использования в геодезических расчетах: большая полуось а = 6378245 м, полярное сжатие α = 1 : 298,3. При этом следует отметить, что полученный референцэллипсоид (референц-эллипсоид Красовского) в наибольшей степени определяет параметры общего земного эллипсоида. Это подтверждают и современные спутниковые измерения.
|
|
|
Таблица 1.1 |
Государство (ученый) |
Год |
Большая полуось, |
Полярное сжатие |
Франция (Деламбер) |
|
м |
|
1800 |
6 375 653 |
1 : 334,0 |
|
Германия (Бессель) |
1841 |
6 377 397 |
1 : 299,2 |
Великобритания (Кларк) |
1866 |
6 378 206 |
1 : 295,0 |
Россия (Слудский) |
1892 |
6 377 494 |
1 : 297,1 |
Россия (Жданов) |
1893 |
6 377 717 |
1 : 299,0 |
С Ш А (Хейфорд) |
1910 |
6 378 388 |
1 : 297,0 |
Россия (Красовский) |
1936 |
6 378 210 |
1 : 298,6 |
Россия (Красовский) |
1940 |
6 378 245 |
1 : 298,3 |
Спутниковые данные |
Совр. |
6 378 137 |
1 : 298,257 |
§ 5. Содержание курса и рекомендации по его изучению
Учебник предназначен для изучения общих вопросов топографии и инженерной геодезии. Вопросы, связанные с общими представлениями о фигуре и размерах Земли, рассмотрены в предыдущем параграфе. Более подробно они будут разъяснены в курсе высшей геодезии.
Что же касается объема изложения разделов топографии и инженерной геодезии, то часть из них, например, вопросы, касающиеся исследований и
12
поверок приборов, организации и выполнения съемок и других видов инже- нерно-геодезических работ и т.п., более подробно изучаются в курсах геодезического инструментоведения, инженерной геодезии, маркшейдерского дела, оценки точности маркшейдерских съемок и др.
Авторы не ставили целью подробное рассмотрение всех вопросов топографии и других дисциплин, и сам учебник не претендует на полное изложение всех вопросов, касающихся производства специальных геодезических работ. Однако приведенные в учебнике основные примеры производства работ и обработки результатов измерений позволят найти решение и в случаях нештатных ситуаций, научат понимать содержание специальной литературы по соответствующим вопросам, обеспечивать выполнение работ строго по действующим руководствам и инструкциям.
Учебник состоит из 16 глав. С содержанием 1-й главы Вы уже ознакомились. Во 2-й главе рассмотрены вопросы, связанные с работой с топографическими картами и планами, даны краткие сведения о картографических проекциях, используемых для составления карт различного назначения. Рассмотрены основные системы координат, используемые в геодезии. В 3-й главе дается сравнительно общая информация о погрешностях измерений, а также приводятся простейшие правила обработки результатов равноточных и неравноточных измерений. Приведен метод получения погрешности функции измеренных величин. 4-я глава посвящена методам создания Государственной геодезической плановой и высотной сети. Приведена информация об опорных съемочных сетях и ходах съемочного обоснования. Приведены формулы оценки точности построения сетей триангуляции, полигонометрии и трилатерации. В 5-й главе рассказано об основных особенностях конструкций оптических геодезических приборов, изложены вопросы, связанные с поверками геодезических приборов и работе с ними. В главе 6 приведены сведения о современных оптико-электронных геодезических приборах, приходящих на смену оптическим приборам. В главе 7 подробно рассмотрены вопросы, связанные с построением съемочного обоснования. Приведены примеры обработки разомкнутых и замкнутых теодолитных ходов. Особое внимание уделено различным вариантам привязки теодолитных ходов к исходным геодезическим сетям. В главе 8 рассмотрены виды топографических съемок местности. Подробно приведены сведения о тахеометрической съемке и о горизонтальной (теодолитной) съемке. 9-я глава содержит сведения о нивелирных работах, производстве трассирования, нивелирования площадей и др. вопросов, связанных с геометрическим нивелированием и другими видами нивелирования. О геодезических разбивочных работах приводится информация в главе 10. В 11-й и 12-й главах изложены вопросы, связанные с геодезическими работами при строительстве различных инженерных сооружений, в том числе – строительстве подземных сооружений. Отдельно рассмотрены геодезические работы на геологических предприятиях (глава 13). Глава 14 посвящена вопросам организации и проведения наблюдений за деформациями инженерных сооружений. Об особенностях точных и высокоточных геодезических измерений
13
рассказано в главе 15. В главе 16 рассмотрены способы и методы уравнивания геодезических построений.
Содержание курса геодезии иллюстрировано примерами расчетов и обработки данных, чаще всего встречающимися на практике. Многие из приведенных примеров Вам встретятся и на лабораторных работах в Ваших заданиях, другие примеры приводятся для подкрепления теоретической части рассматриваемого в учебнике вопроса.
В конце учебника приведен предметный указатель, ссылки которого помогут быстро отыскать то место в учебнике, где наиболее полно можно будет посмотреть о данном понятии или определении.
При изучении курса геодезии, а также и при работе на производстве, Вам придется решать большое число разнообразных ответственных задач, связанных с полевыми измерениями и камеральными расчетами. В связи с этим авторы считают полезным привести отдельные весьма необходимые правила, сформулированные замечательным геодезистом В.В.Витковским [6] еще в начале 1900-х годов:
-держать в порядке полевые журналы, так, чтобы ими мог пользоваться в последствии не только сам наблюдатель, но и другие лица;
-писать разборчиво, чтобы каждый мог понять сущность дела и отыскивать, если понадобится, необходимые числа;
-тщательно изучить и поверить инструменты, а также выработать такой порядок наблюдений, при котором по возможности исключались бы инструментальные погрешности, и получалась бы поверка всех наблюдений;
-не добиваться невозможного на практике полного устранения всех погрешностей и не избегать так называемых приведений (поправок); легче измерить и принять потом в расчет малую величину, чем сделать ее нулем;
-сообразно требуемой точности производить вычисления с различным числом десятичных знаков; не утруждать себя в вычислениях семизначными числами, если по точности можно обойтись и четырехзначными;
-стараться не ошибаться в числовых выкладках; если вычисление не удалось, то не впадать в отчаяние, а утешаться предвкушением удовольствия предстоящего открытия и исправления ошибки; опыт показывает, что если полученная ошибка вынуждает повторить вычисление по той же формуле, то весьма часто ошибаются вновь, и на том же месте;
-неуклонно добиваться поверок (контроля) и не начинать следующей ступени расчетов, пока предыдущая не поверена;
-каждый должен следить за успехами той отрасли знания, которую он избрал поприщем своей деятельности.
Последнее правило касается, в частности, сбора литературы по своей специальности, в том числе и по геодезии. Этим надо заниматься в процессе учебы, с первого курса, поскольку дефицит учебной и научной литературы сейчас весьма ощутим. Тех руководств и инструкций, которыми Вам придется пользоваться на предприятии, будет недостаточно для решения большого круга задач, непосредственно относящихся к геодезическим и маркшейдерским работам. Редко в инструкциях или руководствах даются указания «как
14
