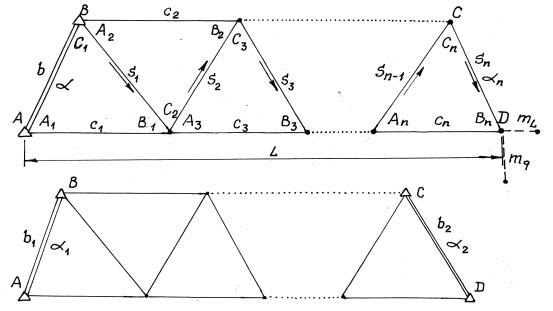
§ 35. Оценка точности построения опорных геодезических сетей

При сгущении геодезических и маркшейдерских сетей на поверхности с целью построения опорных точек вблизи района работ часто выполняют построения, представляющие собой ряды треугольников триангуляции или трилатерации с базисом и азимутом (дирекционным углом) одной стороны (рис. 4.6 а), либо с базисными сторонами и азимутом (дирекционным углом) на концах (рис. 4.6 б), а также системы полигонометрических ходов, чаще имеющих вытянутую форму (рис. 4.5 б). Т.е. сгущение Государственных геодезических сетей высоких классов выполняется теми же методами, которые используются и при построении самих исходных сетей. При выполнении указанных работ необходимо выполнять оценку точности построения тех или иных сетей с учетом метода их построения. Эти вопросы и будут рассмотрены далее в § 36 - § 38.

Рис. 4.6. Ряды треугольников триангуляции и трилатерации. а) с базисом и азимутом на двух его концах; б) с базисом и азимутом на одном его конце.

Для анализа точности построения опорных геодезических плановых сетей введем общие обозначения в соответствии с рис. 4.6:

-b – базис (исходная сторона сети высшего класса);

-s – связующие стороны треугольников;

-с – промежуточные стороны треугольников;

-А и В – связующие углы;

-С – промежуточные углы;

-L – длина диагонали ряда;

-n – число промежуточных сторон в диагонали ряда, отсчитываемых по одному его краю;

-N – число треугольников в ряде;

-средние квадратические погрешности:

93

-- μ ′′ - измерения направлений;

-- m" – измерения углов ( m′′ = μ ′′2 );

-- mα k ² - азимута связующей стороны треугольника k;

-- msk - связующей стороны треугольника k;

-- mL - продольный сдвиг ряда;

-- mq - поперечный сдвиг ряда;

-- М – положение конечной точки ряда относительно начала;

-- mα L ² - азимута диагонали ряда.

При оценках точности построения рядов триангуляции, трилатерации, полигонометрии обычно принимают, что погрешности исходных данных (базиса и азимута исходных сторон) равны нулю. В некоторых случаях этим пренебрегать нельзя, и указанные погрешности учитывают при оценках точности. В последующих параграфах этой главы будут даны расчетные формулы без учета погрешностей исходных данных.

§ 36. Оценка точности построения сетей триангуляции

Рассмотрим два случая построения сетей триангуляции: ряд треугольников с одним базисом на его конце и азимутом (рис. 4.6 а) и ряд треугольников с базисами и азимутами на его концах (рис. 4.6 б).

Ряд треугольников с одним базисом и азимутом на его конце.

Средняя квадратическая погрешность длины связующей стороны ряда триангуляции.

Формула для относительной погрешности связующей стороны имеет

вид:

94

Средняя квадратическая погрешность азимута связующей стороны ряда.

В зависимости от способа уравнивания (глава 16) углов в треугольниках для оценки вероятной погрешности азимута связующей стороны используются разные формулы:

- при уравнивании за условие направлений:

Продольный и поперечный сдвиги ряда триангуляции.

Оценка продольного сдвига ряда производится для равносторонних треугольников при уравнивании в них углов любым способом. Для указанной оценки используют формулу:

В формуле (4.6) знак «плюс» при 3n берется при четном N (числе треугольников), знак «минус» - при нечетном.

Поперечный сдвиг ряда равносторонних треугольников определяется

средняя квадратическая погрешность азимута диагонали ряда – по формуле

Погрешность положения конечной точки ряда относительно его начала:

Ряд треугольников с двумя базисами и азимутами на его концах.

В данном ряду триангуляции менее надежно определяется длина стороны и ее азимут, находящейся в середине ряда. В связи с этим приводимые ниже формулы дают наибольшие значения при n = k = 0,5N и меньшие значения для треугольников, близких к базисным сторонам.

Средняя квадратическая погрешность связующей стороны ряда

где

95

в логарифмической форме.

Средняя квадратическая погрешность азимута связующей стороны

равна

Значения δ L , mα k и M вычисляют соответственно по формулам (4.9), (4.10), (4.11).

Всплошной сети триангуляции точность определения дирекционных углов и длин сторон, удаленных от границы сети не менее чем на 4-5 треугольников, примерно одинаковая во всех частях сети. При решении задачи сгущения геодезических и маркшейдерских сетей такие построения встречаются в исключительных случаях, при весьма небольшом числе исходных пунктов, расположенных на больших расстояниях друг от друга.

Всплошных сетях триангуляции погрешность дирекционного угла

оценивают по формуле

Среднюю квадратическую погрешность направлений mT получают по формуле

Продольный и поперечный сдвиг концов диагоналей, соединяющих пункты, разделенные n треугольниками, примерно равны друг другу:

Следует иметь ввиду, что приведенные формулы оценки точности построения рядов триангуляции и геодезических сетей триангуляции, как и формулы других геодезичесих построений, дают предварительные величины, по которым принимаются решения о методике выполнения работ. При практическом выполнении фактические значения погрешностей элементов построений могут отличаться в ту или другую сторону.

96