
- •Предисловие
- •Глава 1. Вводная часть
- •§ 1. Предмет и задачи геодезии
- •§ 2. Краткие исторические сведения
- •§ 3. Единицы измерений, применяемые в геодезии
- •§ 4. Фигура и размеры Земли
- •§ 5. Содержание курса и рекомендации по его изучению
- •Глава 2. Топографические карты и планы
- •§ 6. Влияние кривизны Земли на измеренные расстояния
- •§ 7. Краткие сведения о картографических проекциях
- •§ 8. Общие сведения о топографических картах и планах
- •§ 9. Система географических координат
- •§ 10. Равноугольная поперечно-цилиндрическая проекция Гаусса-Крюгера
- •§ 11. Разграфка и номенклатура топографических карт и планов
- •§ 12. Зональная система плоских прямоугольных координат Гаусса
- •§ 13. Перевычисление координат из зоны в зону
- •§ 14. Система высот
- •§ 15. Условные знаки топографических карт и планов
- •§ 16. Изображение рельефа на топографических картах и планах
- •§ 17. Ориентирование
- •§ 18. Решение некоторых задач с использованием топографической карты
- •18.1. Измерение расстояний
- •18.2. Определение географических и прямоугольных координат
- •18.3. Ориентирование линий
- •18.4. Ориентирование карты на местности
- •18.5. Определение высот точек
- •18.6. Построение профиля
- •18.7. Построение линии заданного уклона
- •18.9. Определение площадей на топографических картах и планах
- •§ 19. Виды измерений
- •§ 20. Классификация погрешностей измерений
- •§ 21. Свойства случайных погрешностей
- •§ 22. Среднее арифметическое
- •§ 23. Средняя квадратическая погрешность
- •§ 24. Средние квадратические погрешности функций измеренных величин
- •§ 25. Обработка ряда равноточных измерений одной величины
- •§ 26. Об учете систематических погрешностей в измерениях
- •§ 27. Средняя квадратическая погрешность двойных равноточных однородных измерений
- •§ 28. Понятие о весе результата измерения
- •§ 29. Средняя квадратическая погрешность единицы веса и арифметической середины
- •§ 30. Обработка ряда неравноточных измерений одной величины
- •Глава 4. Государственные геодезические сети
- •§ 31. Назначение Государственных геодезических сетей
- •§ 32. Классы геодезических сетей
- •§ 33. Методы построения Государственных геодезических сетей
- •§ 34. Закрепление пунктов геодезических сетей
- •§ 35. Оценка точности построения опорных геодезических сетей
- •§ 36. Оценка точности построения сетей триангуляции
- •§ 37. Оценка точности построения звена полигонометрии
- •§ 38. Оценка точности построения сетей трилатерации
- •Глава 5. Геодезические приборы
- •§ 39. Классификация геодезических приборов
- •§ 40. Теодолиты
- •§ 41. Зрительные трубы
- •§ 42. Уровни и компенсаторы наклона
- •§ 43. Устройство теодолита
- •§ 44. Установка теодолита в рабочее положение
- •§ 45. Измерение горизонтальных углов и углов наклона
- •45.1. Способ приемов
- •45.2. Способ повторений
- •45.3. Способ круговых приемов
- •45.4. Измерение углов наклона
- •§ 46. Поверки теодолитов
- •§ 47. Нивелиры
- •§ 48. Устройство нивелира
- •§ 49. Нивелирные рейки
- •§ 50. Установка нивелира в рабочее положение
- •§ 51. Измерение превышений
- •§ 52. Поверки нивелиров
- •§ 53. Приборы для линейных измерений
- •§ 54. Гироскопические приборы
- •§ 55. Приборы для поиска подземных коммуникаций
- •Глава 6. Оптико-электронные геодезические приборы
- •§ 56. Общие замечания
- •§ 57. Краткие сведения о лазерных источниках излучения
- •§ 58. Электромагнитные дальномеры
- •§ 59. Светодальномеры
- •§ 60. Интерферометры
- •§ 61. Угломерные приборы
- •§ 62. Электронные тахеометры
- •§ 63. Электронные нивелиры
- •§ 64. Лазерные приборы
- •Глава 7. Построение съемочного обоснования
- •§ 65. Назначение и виды теодолитных ходов
- •§ 66. Прямая и обратная геодезические задачи на плоскости
- •§ 67. Взаимосвязь дирекционных углов с измеренными на местности горизонтальными углами
- •§ 68. Привязка теодолитных ходов
- •68.1. Способ примыкания
- •68.2. Прямая угловая засечка
- •68.3. Линейная засечка
- •68.4. Обратная угловая засечка
- •68.5. Комбинированные засечки
- •68.6. Задача П.А.Ганзена
- •§ 69. Особые системы теодолитных ходов
- •§ 70. Снесение координат с вершины знака на землю
- •§ 71. Определение элементов приведения и редукции
- •§ 72. Привязка теодолитных ходов к стенным геодезическим знакам
- •§ 73. Спутниковые методы определения координат
- •§ 74. Организация полевых работ при построении съемочного обоснования
- •74.1. Рекогносцировка и закрепление точек съемочного обоснования
- •74.2. Подготовка абрисов горизонтальной съемки
- •74.3. Поверки теодолита и нивелира
- •74.4. Компарирование мерных приборов
- •74.5. Измерение длин линий
- •74.6. Измерение горизонтальных углов и углов наклона
- •§ 75. Вычисления в разомкнутом теодолитном ходе
- •75.1. Предварительные вычисления
- •75.2. Обработка результатов угловых измерений
- •75.3. Вычисление приращений координат и оценка точности хода
- •75.4. Рекомендации к поиску вероятных погрешностей в измерениях и вычислениях при обработке ведомости координат
- •75.5. Уравнивание приращений координат и вычисление координат точек хода
- •75.6. Обработка ведомости высот
- •§ 76. Вычисления в замкнутом теодолитном ходе
- •76.1. Оценка точности угловых измерений и вычисление дирекционных углов
- •76.2. Вычисление приращений координат и оценка точности хода
- •76.3. Уравнивание приращений координат и вычисление координат точек хода
- •76.4. Обработка ведомости высот
- •§ 77. Обработка диагонального хода
- •Глава 8. Топографические съемки
- •§ 78. Назначение и виды топографических съемок
- •§ 79. Понятие о цифровой модели местности
- •§ 80. Теодолитная съемка
- •§ 81. Тахеометрическая съемка
- •§ 82. Составление плана местности по результатам топографической съемки
- •82.2. Нанесение на план точек съемочного обоснования
- •82.3. Нанесение на план результатов тахеометрической съемки
- •82.4. Рисовка рельефа и ситуации
- •82.5. Построение на плане ситуации по результатам теодолитной съемки
- •Глава 9. Нивелирные работы
- •§ 83. Способы и методы нивелирования
- •§ 84. Способы геометрического нивелирования
- •§ 85. Основные источники погрешностей геометрического нивелирования
- •§ 86. Техническое нивелирование
- •§ 87. Трассирование
- •§ 88. Расчет и разбивка главных точек кривых на трассе
- •§ 89. Нивелирование поперечных профилей
- •§ 90. Обработка результатов нивелирования трассы
- •§ 91. Построение профиля трассы
- •§ 92. Построение проектной линии
- •§ 93. Построение поперечного профиля и проектного полотна дороги
- •§ 94. Нивелирование площадей
- •Глава 10. Геодезические разбивочные работы
- •§ 95. Назначение и организация разбивочных работ
- •§ 96. Построение на местности проектного горизонтального угла
- •§ 97. Построение на местности проектного расстояния
- •§ 99. Способы разбивочных работ
- •§ 100. Расчет разбивочных элементов
- •§ 101. Разбивочные работы при трассировании
- •§ 102. Разбивка фундаментов инженерных сооружений
- •§ 103. Оценка точности разбивочных работ
- •Глава 11. Геодезические работы в строительстве
- •§ 104. Общие положения
- •§ 105. Краткие сведения об объектах строительства
- •§ 106. Геодезические работы при строительстве промышленных сооружений
- •§ 107. Геодезические работы при строительстве гражданских зданий
- •§ 108. Геодезические работы при строительстве дорог и мостовых сооружений
- •§ 109. Геодезические работы при планировании и застройке населенных пунктов
- •§ 110. Геодезические работы при строительстве подземных коммуникаций
- •§ 111. Геодезические работы при строительстве гидротехнических сооружений
- •Глава 12. Геодезические работы в подземном строительстве
- •§ 115. Горизонтальная соединительная съемка
- •115.2. Горизонтальная соединительная съемка через один шахтный ствол
- •§ 116. Вертикальная соединительная съемка
- •§ 117. Подземная горизонтальная съемка
- •§ 118. Подземная вертикальная съемка
- •§ 119. Геодезические разбивочные работы в подземном строительстве
- •§ 120. Задачи и содержание топографо-геодезических работ
- •§ 121. Точность геодезических работ
- •§ 122. Создание топографических карт и планов
- •§ 123. Разбивка геодезических сеток и профильных линий
- •§ 124. Разбивочные работы при проведении геологической разведки
- •§ 126. Виды деформаций инженерных сооружений
- •§ 127. Задачи наблюдений и организация работ
- •§ 128. Геодезические знаки и их конструкции
- •§ 129. Размещение геодезических знаков на инженерных сооружениях
- •§ 130. Точность измерения деформаций
- •§ 131. Периодичность наблюдений
- •§ 132. Наблюдения за вертикальными перемещениями
- •§ 133. Наблюдения за горизонтальными смещениями
- •§ 134. Наблюдения за кренами
- •§ 135. Наблюдения за деформациями земной поверхности
- •§ 136. Разработка методики наблюдений
- •§ 137. Обработка и анализ результатов наблюдений
- •Глава 15. Особенности точных и высокоточных измерений
- •§ 138. Основные группы погрешностей измерений
- •§ 139. Учет влияния рефракции атмосферы
- •§ 140. Высокоточное и точное геометрическое нивелирование
- •§ 141. Нивелирование I класса
- •§ 142. Нивелирование II класса
- •§ 143. Нивелирование III и IV классов
- •§ 144. Особенности точного и высокоточного нивелирования при наблюдениях за деформациями
- •§ 145. Высокоточные и точные угловые измерения
- •§ 146. Высокоточные и точные измерения в схемах микротриангуляции, микротрилатерации и короткобазисной полигонометрии
- •Глава 16. Уравнивание геодезических построений
- •§ 147. Основные задачи уравнительных вычислений
- •§ 148. Метод наименьших квадратов
- •§ 149. Классификация основных способов уравнивания
- •§ 150. Основные геометрические условия, возникающие в построениях
- •150.1. Условие фигуры
- •150.2. Условие горизонта
- •150.3. Условие суммы углов
- •150.4. Условие дирекционных углов
- •150.5. Условие сторон
- •150.6. Условие полюса
- •150.7. Условие координат
- •§ 151. Методы решения систем линейных нормальных уравнений
- •151.1. Способ последовательной подстановки
- •151.2. Способ матричных преобразований
- •151.3. Решение систем линейных уравнений по алгоритму Гаусса
- •151.4. Способ краковянов
- •§ 152. Коррелатный способ уравнивания
- •§ 153. Примеры коррелатного способа уравнивания
- •153.1. Уравнивание углов в полигоне
- •153.2. Уравнивание системы нивелирных ходов с несколькими узловыми точками
- •153.3. Уравнивание полигонометрического хода
- •153.4. Уравнивание системы полигонометрических ходов с двумя узловыми точками
- •153.5. Уравнивание триангуляции
- •153.6. Уравнивание триангуляции по условию координат
- •§ 154. Параметрический способ уравнивания
- •§ 155. Примеры параметрического способа уравнивания
- •155.1. Уравнивание углов в полигоне
- •155.2. Уравнивание системы нивелирных ходов с несколькими узловыми точками
- •155.3. Уравнивание полигонометрического хода
- •155.4. Уравнивание системы полигонометрических ходов с двумя узловыми точками
- •155.5. Уравнивание направлений в триангуляции
- •§ 156. Способ раздельного уравнивания
- •156.1. Уравнивание полигонометрического хода
- •156.2. Система полигонометрических ходов с одной узловой точкой
- •156.3. Система нивелирных ходов с одной узловой точкой
- •§ 157. Способ эквивалентной замены
- •§ 158. Способ полигонов В.В.Попова
- •§ 159. Способ последовательных приближений
- •§ 160. Оценка точности уравненных элементов и их функций
- •160.1. Общие положения
- •160.2. Оценка точности при уравнивании коррелатным способом
- •160.3. Оценка точности при уравнивании параметрическим способом
- •Предметный указатель
- •Список литературы
- •Оглавление
|
|
|
|
|
|
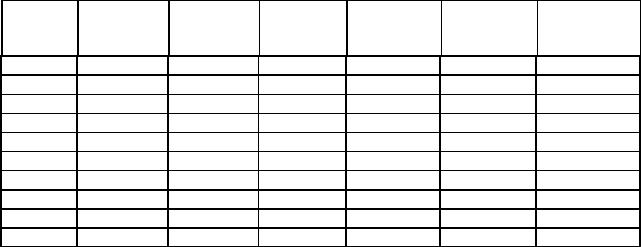
Таблица 3.4 |
№№ п/п |
1-е |
2-е |
Разности, |
Система- |
Случайная |
|
|
измерение, |
измерение, |
di , м |
тическая |
погреш- |
δi2 |
|
хi , м |
хi´ , м |
|
погреш- |
ность, δi |
х10-6 |
|
|
|
|
ность, qi |
|
|
1 |
647,263 |
647,261 |
+ 0,002 |
- 0,005 |
+ 0,007 |
49 |
2 |
624,850 |
624,857 |
- 0,007 |
- 0,005 |
- 0,002 |
4 |
3 |
636,304 |
636,315 |
- 0,011 |
- 0,005 |
- 0,006 |
36 |
4 |
652,842 |
652,844 |
- 0,002 |
- 0,005 |
+ 0,003 |
9 |
5 |
638,219 |
638,209 |
- 0,010 |
- 0,005 |
- 0,005 |
25 |
6 |
625,347 |
625,346 |
+ 0,001 |
- 0,005 |
+ 0,006 |
36 |
7 |
644,936 |
644,936 |
0,000 |
- 0,005 |
+ 0,005 |
25 |
8 |
650,027 |
650,015 |
- 0,012 |
- 0,005 |
- 0,007 |
49 |
9 |
641,006 |
641,013 |
- 0,007 |
- 0,005 |
- 0,002 |
4 |
§ 28. Понятие о весе результата измерения
До сих пор мы говорили о результатах измерений, точность которых (степень доверия к ним) была одинаковая, весьма близкая по величине. Строго говоря, в природе измерений не существует равноточных величин. Обеспечить это весьма сложно, да во многих случаях и нет в этом необходимости. К равноточным измерениям можно отнести все результаты, погрешности которых не выходят за пределы допустимой величины, например, двойной средней квадратической погрешности.
Часто приходится иметь дело с разнородными величинами. Например, при выполнении геодезических измерений использовать результаты длин линий, которые значительно отличаются по величине, либо измерены разными по точности приборами, либо однородные величины в группе измерены равноточно, но с разным числом измерений в группах и т.п. В этом случае, при оценке точности, говорят о неравноточных измерениях.
Если в качестве веса результата измерения взять число, которое характеризует точность, то по смыслу слова вес можно сказать, что, чем больше вес результата, тем выше его точность (тем меньше погрешность, с которой получен данный результат). Т.е. вес находится в обратно пропорциональной зависимости от погрешности результата. Пусть точность измерения какойлибо величины характеризуется средней квадратической погрешностью m, тогда вес Р определяют как отношение
Р = |
с2 |
(3.37) |
|
m2 |
|||
|
|
Значение с может быть любым, кроме нуля, но для анализируемой группы результатов измерений его принимают равным примерно среднему значению m по группе, поэтому значения весов результатов измерений не будут слишком большими или слишком маленькими.
Очевидно, что величина СКП зависит от числа измерений, а это значит, что от числа измерений зависит и вес: чем с большим числом измерений получен тот или иной результат, тем больше его вес.
Уже при обработке ряда равноточных измерений мы сталкивались с результатами, имеющими разный вес. Если принять за единичный вес результат одного измерения, то среднее арифметическое будет получено с большим
80

весом, причем вес его будет в n раз больше, чем вес результата одного измерения.
Предположим, что при равноточных измерениях одной и той же величины Х (заранее неизвестной) выполнено три серии по ni наблюдений в каждой:
n1, n2, n3, причем n1> n2> n3. Примем значение с2 в формуле (3.37) равным n1. Поскольку значение СКП обратно пропорционально корню квадратному из
числа измерений, то квадрат СКП будет обратно пропорционален числу измерений. В связи с этим формулу (3.37) можно переписать в виде
P = |
ni |
, |
(3.38) |
|
|||
|
no |
|
|
где no = 
 с .
с .
В рассматриваемом случае Р1 = 1, Р2 = n2 /n1 , Р3 = n3 /n1. Это говорит о том, что серии измерений неравноточны между собой.
Обозначим результаты измерений в сериях 1, 2 и 3 как x1i , x2i , x3i и вычислим средние арифметические значения измеренной величины в каждой
из серий: x1о , x2о и x3о по формуле (3.14).
Для всей группы измерений значение арифметической середины xо определится с учетом их весов из выражения
xo = |
x1o P1 + x2o P2 + x3o P3 |
= |
[xo P] |
||
|
[P] |
||||
P + P + P |
|||||
|
1 |
2 |
3 |
|
(3.39) |
|
|
|
|
|
|
Аналогичная формула получится и для случая n серий измерений.
Из формулы (3.39) следует, что вес арифметической середины равен сумме весов всех измерений, входящих в серии.
Веса всех измерений можно изменить в одинаковое число раз. От этого значение арифметической середины не изменится. Т.е. в качестве no можно взять и другое число, отличное от n1, n2 и n3. Это число (с, no и др.) называют
единицей веса.
Для оценки весов неравноточных измерений или групп неравноточных измерений используют различные приемы. Так, если известны средние квадратические погрешности в группах измерений, то в качестве единицы веса может быть выбрана любая из известных СКП, либо примерно среднее ее значение. Вес результата измерения в группе в этом случае определится по формуле (3.37).
Внекоторых случаях в качестве единицы веса используют число измерений в группе. Даже если предположить, что каждая из величин в каждой из групп измеряется равноточно, то при разных числах измерений в группе образуются результаты средних арифметических, неравноточных между собой. Здесь приемлемо использовать для вычисления весов формулу (3.38).
Вкачестве погрешности единицы веса может выступать и, например, измеряемое расстояние, если погрешность его определения функционально зависит от его величины (практически это и имеет место). В зависимости от вида указанной функции единицей веса может быть как непосредственно длина линии, так и корень квадратный из длины линии.
81

При измерении горизонтальных углов на местности в некоторых случаях в качестве единицы веса направления (отсчета по горизонтальному кругу теодолита) используют величину этого направления, поскольку погрешность направления зависит от погрешности установки оси теодолита над вершиной измеряемого угла (погрешность центрирования). Чем короче расстояние (сторона угла), тем больше погрешность направления (прямая пропорциональная зависимость). В этом случае в качестве единицы веса при вычислении весов направлений следует брать квадрат длины стороны.
§ 29. Средняя квадратическая погрешность единицы веса и арифметической середины
Средняя квадратическая погрешность единицы веса μ характеризует погрешность результата измерения, вес которого равен единице.
В этом случае формулу (3.37) можно представить в виде
Pi = |
|
μ |
2 |
. |
(3.40) |
|||
|
|
|
||||||
|
|
2 |
||||||
Из (3.40) найдем |
mi |
|
||||||
|
|
μ |
|
|||||
mi = |
|
|
(3.41) |
|||||
|
|
|
|
|
|
|
||
|
|
|
Pi |
|||||
|
|
|
|
|
||||
Таким образом, СКП результата измерения равна СКП единицы веса, деленной на корень квадратный из веса этого измерения.
Если выполнено n серий измерений, то СКП единицы веса, характеризующую все измерения, можно найти по формуле
μ |
= |
|
[m2 P] |
|
(3.42) |
|
|
n |
|
||||
|
|
|
|
|
||
Если выполнено n серий измерений известной величины Х, то |
|
|||||
μ |
= |
[ 2 P] |
|
, |
(3.43) |
|
|
n |
|||||
|
|
|
|
|
||
где = (хоi – X) – разность среднего арифметического серии i и истинного значения измеряемой величины.
Если выполнено n серий измерений неизвестной величины, то
μ = |
[ν 2 P] |
, |
(3.44) |
(n − 1) |
|||
|
|
|
где ν = (хоi – хо) – уклонения среднего арифметического серии i от арифметической середины всей группы измерений.
В соответствии с формулой (3.43) СКП арифметической середины Мо может быть получена из выражений:
M O = |
[ν 2 P] |
= |
μ |
. |
(3.45) |
|
(n − 1)[P] |
[P] |
|||||
|
|
|
|
Т.е., СКП арифметической середины в корень квадратный из суммы весов всех серий измерений меньше, чем СКП единицы веса.
82
§ 30. Обработка ряда неравноточных измерений одной величины
Рассмотрим пример обработки результатов неравноточных измерений одной величины.
Пример 3.7. Выполнено 6 серий измерений длины линии, равноточных в каждой из серий, но неравноточных между сериями (обработка результатов - табл. 3.5).
Вычисление весов серий. Принимаем nо = n3 = 5. Значения весов остальных серий находим по формуле (3.38). Сумма весов равна [Р] = 6,60.
По формуле (3.39) находим арифметическую середину
xo = 76,835 × 1,40 + 76,841 0,60×+ ... + 76,837 × 1,60 = 76,8378 м 1,40 + 0,60 + ... + 1,60
Вычисляем уклонения средних арифметических в сериях от арифметической середины и произведения νi Pi . Здесь контролем вычислений является равенство [νi Pi] = 0. В примере [νi Pi] = +0,00014, что незначительно отличается от нуля. Это вызвано результатом округлений исходных величин.
Образуем произведения νi2Pi и получим их сумму [νi2Pi] = 23,784 · 10-6.
По формуле (3.44) находим СКП единицы веса (т.е. серии измерений, вес которой принят нами за единицу – серия № 3): μ = 0,0022 м.
По формуле (3.45) находим СКП арифметической середины: МО = 0,0008 м. Таким образом, значение измеренной величины равно: (76,8378 ± 0,0008) м. По формуле (3.41) определим СКП в сериях измерений:
m1 = 0,0019 м; m2 = 0,0028 м; m3 = μ = 0,0022 м; m4 = 0,0020 м; m5 = 0,0025 м; m6 = 0,0017 м.
|
|
|
|
|
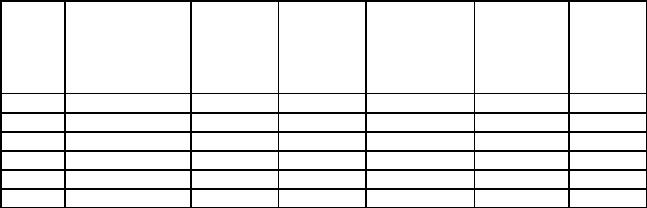
Таблица 3.5 |
|
№№ |
Среднее |
Число |
Веса |
|
|
νi2Pi |
арифметическое |
измерений |
измере- |
Уклонения |
|
||
серий |
в серии |
в серии, ni |
ний в |
νi = xoi – xo |
νi Pi |
|
|
измерений: хоi, |
|
серии, Рi |
|
|
х 10-6 |
|
м |
|
|
|
|
|
1 |
76,835 |
7 |
1,40 |
-0,0028 |
-0,00390 |
10,976 |
2 |
76,841 |
3 |
0,60 |
+0,0032 |
+0,00192 |
6,144 |
3 |
76,838 |
5 |
1,00 |
+0,0002 |
+0,00020 |
0,040 |
4 |
76,839 |
6 |
1,20 |
+0,0012 |
+0,00144 |
1,728 |
5 |
76,840 |
4 |
0,80 |
+0,0022 |
+0,00176 |
3,872 |
6 |
76,837 |
8 |
1,60 |
-0,0008 |
-0,00128 |
1,024 |
83
