Чаще всего высоты точек по карте определяют оценкой их положения относительно горизонталей «на глаз». Это связано с тем, что погрешность построения горизонталей на карте составляет примерно 1/3 от высоты сечения рельефа, а погрешность оценки «на глаз» положения точки значительно меньше, порядка 1/10 от величины заложения.

Точка D (хребет). На этом фрагменте имеется подписанная высота точки местности (101,5 м). Учитывая высоту сечения рельефа (2 м), соседние с точкой 101,5 м горизонтали имеют высоты 100 и 102 м (повышение рельефа в сторону точки D). Точка D находится между горизонталью 104 м и полугоризонталью 103 м, ближе к основной горизонтали. Оценкой «на глаз» НD = 104 – 0,33 = 103,67 м = 103,7 м.

Точка Е (лощина). При высоте сечения рельефа 2,5 м точка Е находится между горизонталями 175 и 172,5 м посредине между ними. Таким образом, НЕ = 175,00 – 1,25 = 173,75 м.

Точки F и G (седловина). При высоте сечения рельефа 5 м соседняя с вершиной горы горизонталь, кратная 5 м, имеет высоту 65 м.

Переместимся в точку седловины. Первые по основанию гор горизонтали, находящиеся выше точки седловины, имеют высоту 55 м. Точка F находится «на глаз» на 1,5 м выше горизонтали 55 м, т.е. НF = 56,5 м. Точка G находится «на глаз» посредине между горизонталями 40 и 45 м, значит НG = 42,5 м.

18.6. Построение профиля

Профиль – это вертикальный разрез рельефа местности по заданному направлению.

Топографические профили местности используются для решения большого числа различных инженерных задач: при составлении предварительных проектов строительства инженерных сооружений линейного типа, при составлении геологических разрезов, при определении на местности линий видимости между выбранными точками, для составления описания рельефа по выбранному маршруту и др.

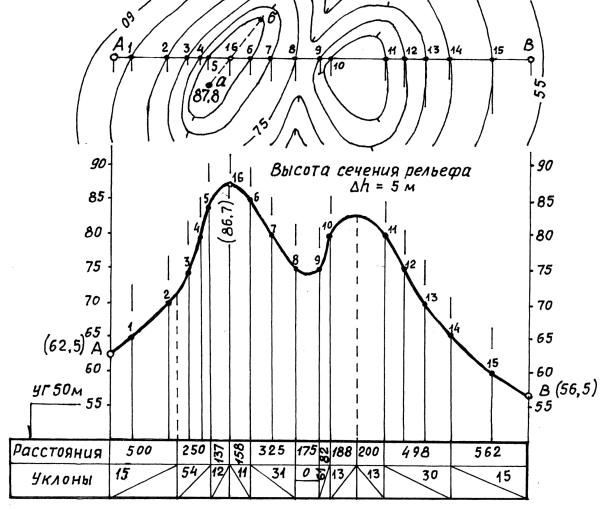
Построение профиля по направлению АВ показано на рис. 2.25.

1.Прочертить карандашом на карте линию АВ, направление которой задано тем или иным способом.

2.Оценить максимальную и минимальную высоту по линии профиля.

НМАХ ~ 88 м ; НMIN ~ 55 м.

3. Задать горизонтальный и вертикальный масштабы профиля.

Горизонтальной линией профиля является ось расстояний, вертикальной линией – ось высот. Масштабы профиля, построенного по топографической карте, по высоте и расстояниям различные. Обычно горизонтальный масштаб профиля равен масштабу топографической карты, на которой он строится, а вертикальный масштаб принимают в 10 раз крупнее горизонтального. Например, масштаб карты 1:50000. Следовательно, горизонтальный масштаб профиля равен 1:50000, а вертикальный масштаб – 1:5000. В некоторых случаях, для большей наглядности, применяют более крупные масштабы высот, либо укрупняют и горизонтальный масштаб. В любом случае для основания масштаба рекомендуется выбирать числа: 1; 2; 2,5; 5 (1:1000, 1:200, 1:50 и т.п.).

Горизонтальный масштаб 1:25000 (в 1 см 250 м)

Вертикальный масштаб 1:2500 (в 1 см 25 м). На рисунке вертикальный масштаб принят 1:500 (в 1 см 5 м).

4. Построить оси координат профиля и оцифровать их в соответствии с выбранными горизонтальным и вертикальным масштабами.

55

Указать высоту условного горизонта.

Условный горизонт (УГ) – это линия, абсолютная высота которой на графике профиля подбирается так, чтобы между нижней точкой профиля и линией условного горизонта оставалось место для нанесения другой информации, в отношении которой строится сам профиль.

Рис. 2.25. Построение профиля местности по карте

Условный горизонт УГ = 50 м.

5.Отложить на горизонтальной линии отрезки, соответствующие пересечениям горизонталей с линией профиля, а также точек пересечения линии профиля с объектами ситуации (дорогами, линиями связи, объектами гидрографии, границами лесов и т.п.).

6.Нанести отмеченные точки на чертеже в соответствии с их абсолютными высотами. Полученные точки соединить плавной линией.

В некоторых случаях на линии профиля можно определить высоты дополнительных точек. Если, например, точка находится между горизонталями, то ее высоту легко найти интерполированием заложения, как это пояснялось в разделе 18.5:

56

где НГ – высота горизонтали; а – заложение; m – расстояние от горизонтали до точки линии профиля. Т.е. определяется аналогично определению высоты точки С в предыдущем разделе.

При пересечении лощины (хребта) дополнительную точку определяют на линии водослива (водораздела) также методом интерполирования.

При пересечении седловины для точки седловины принимают, что она находится на половине высоты сечения рельефа от ближайшей к ней горизонтали.

Для точки 16, находящейся на вершине горы, определение высоты связано с построением однородного отрезка аб. В этом случае превышение точки б по отношению к вершине горы будет отрицательным:

hб = 85,0 – 87,8 = - 2,8 м.

Длина отрезка аб равна 26 мм, отрезка а16 – 10 мм. Из пропорции находим, что h16 = - 2,8 м (10мм/26 мм) = - 1,1 м. Следовательно, высота точки 16 будет равна H16 = 87,8 – 1,1 = 86,7 м.

Если высоты точек профиля определяют дополнительно, то их значения записывают в скобках.

В случаях, когда высота точки не может быть определена, точки с известными высотами соединяют на профиле линией сопряжения, характеризующей форму рельефа в данном месте.

7. В сетке профиля выделить «на глаз» однородные склоны и вычислить для них уклоны. (Об определении уклонов см. п. 18.7).

Характерными точками рельефа и ситуации являются точки перегибов рельефа, линии водоразделов и водосливов (тальвеги), седловины, вершины гор (холмов), дна котловин (ям), пересечения с объектами линейного типа, гидрографией, а также и другие точки, представляющие интерес для исполнителя.

18.7. Построение линии заданного уклона

Обычно решают задачу построения линии предельного (возможного максимального) уклона (угла наклона).

Углом наклона ν является угол в вертикальной плоскости между плоскостью горизонта и направлением на данную точку, либо направлением ли-

Вправом нижнем углу карты приводят график заложений, построенный

сиспользованием формулы (2.26) для установленной для данной карты высоты сечения рельефа.

57

Для однородной линии тангенс угла наклона равен отношению превышения h крайних точек отрезка к горизонтальному проложению d между ними, т.е

В частном случае, для определения уклона местности между соседними сплошными горизонталями по заложению между ними можно записать, что

тангенса угла наклона (0,0124, 0,005 и т.п.). Для сокращения записи значения уклона часто записывают его увеличенными на 1000 (0,002 → 2; 0,0236 → 23,6 и т.п.), при этом при произношении величины уклона обязательно добавляют слово «тысячных». Часто величину уклона указывают в про-центах.

Пример 2.16. Определение уклона линии (рис. 2.25).

Решение.

Для первого отрезка однородной линии профиля А-2 горизонтальное проложение равно 500 м, превышение точки 2 относительно точки А положительное (в строке «уклоны» это отмечено соответствующим наклоном) 70,0 – 62,5 = +7,5 м. Уклон линии равен +7,5/500 = +0,015 = 15 тысячных. Например, для однородного отрезка 6-8, имеющего горизонтальное проложение 325 м, превышение отрицательное, -10 м. Уклон будет равен -10/325 = - 0,031 = -31 тысячная.

Как следует из формулы (2.26), увеличение угла наклона или уклона соответствует уменьшению величины заложения. И наоборот.

Значению предельного уклона iпред соответствует и предельное значение угла наклона νпред, а значит и предельная величина заложения апред. Таким образом, при построении линии заданного уклона следует выбирать те направления на местности, по которым величина уклона не будет больше предельного, либо величина заложения не будет меньше предельного его значения.

Порядок построения линии с заданным значением предельного уклона следующий (рис. 2.26).

Предположим, что необходимо построить на карте линию АВ со значением предельного уклона i = 0,026 (ν = 1,5о), соответствующего предельному значению заложения, показанного на рисунке. От точки А до точки 1 движение выполняется по линии АВ. Далее руч. Гремячий пересекается под прямым углом к линии водотока до точки 2. От точки 2 перемещение к точке В может выполняться по двум вариантам (1 и 2). Здесь очевидно, что вариант 1 является оптимальным, исходя из длины общей линии АВ. Однако следует иметь в виду, что при оценке экономической целесообразности оптимальным может оказаться и второй вариант. Например, при изысканиях линейных сооружений (дорог, линий связи и т.п.) более выголным может оказаться путь в обход лесного массива.

58

Рис. 2.26. Построение на карте линии заданного уклона

Возможны и другие варианты, например, вариант 3. Однако при постановке задачи проектирования кратчайшего расстояния этот вариант отпадает.

18.8. Построение границы водосборного бассейна и зоны затопления

Определение границы водосборного бассейна. Водосборный бассейн представляет собой ту часть земной поверхности, с которой вода, поступающая из атмосферы, стекает по склонам неровностей и собирается затем в одной точке водотока (лощины, оврага, реки и т.п.). При этом примем, что поступающая из атмосферы вода не будет поглощаться грунтом, а будет эвакуироваться по поверхности земли.

Границей водосборного бассейна являются линии водоразделов.

Для построения границы водосборного бассейна необходимо от заданной точки водотока А (рис. 2.27) подняться по линиям, перпендикулярным к горизонталям, до ближайшей водораздельной линии. Далее граница продолжается непосредственно по линиям водоразделов до их замыкания.

Используют границы водосборных бассейнов для последующего определения площади бассейна, необходимой при расчетах возможных притоков воды к отверстиям водопропускных систем под дорогами, при проектировании аэродромов и в других случаях.

Водораздельные линии строят также перпендикулярно к горизонталям по хребтам через вершины гор и точки седловин.

Построение зоны затопления

выполняют при проектировании

59