Величины поправок по ходам (1) и (5) получаются как разность между уравненным значением высоты узловой точки А и ее высотами, полученными по соответствующим ходам:

Аналогично для ходов (2) и (7) через узловую точку С:

по каждому из замкнутых полигонов и разомкнутому ходу. Для этого занесем на схему нивелирных ходов значения полученных поправок. Знак поправки на схеме устанавливают в соответствии с направлением движения.

§158. Способ полигонов В.В.Попова

Вэтом примере используем схему нивелирных ходов, рассмотренную в

§157.

1. В крупном масштабе привести указанную схему нивелирных ходов (рис. 16.18), на которой следует отметить и пронумеровать независимые

где N – число замкнутых неперекрывающихся полигонов (N = 3); q – число исходных пунктов (q = 2). Т.е. r = 4.

2. На схеме указать длины ходов, направление обхода полигонов (для всех: либо по часовой стрелке, либо против часовой стрелки). Внутри полигонов (под номером полигона) построить таблички невязок, в которые будут заноситься величины невязок в приближениях. С внешней стороны каждого хода разместить таблички поправок в измеренные превышения данного хода (для смежных полигонов вычерчиваются для одного и того же хода две таблички поправок – с двух сторон хода).

490

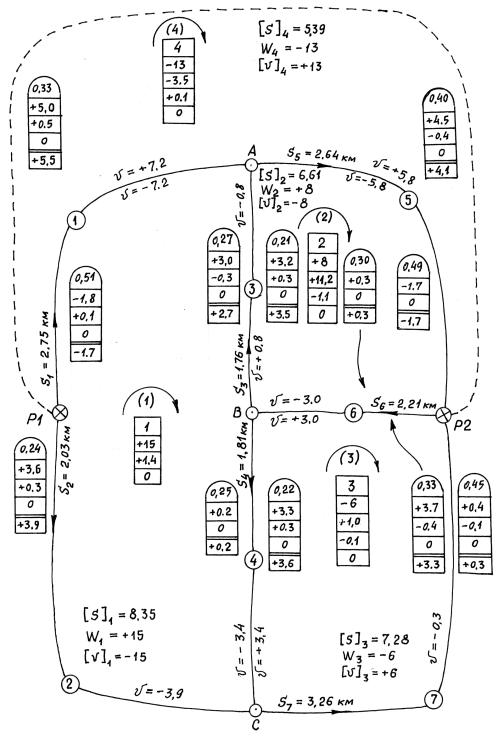
Рис. 16.18. Уравнивание способом полигонов (В.В.Попова)

3. Распределить невязки W в ходах пропорционально длинам ходов по формуле

Веса превышений рi = si 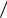å s( j )

записываются в табличке поправок в верхней полукруглой графе (с округлеением до 0,01). Сумма весов для полигона должна быть равна 1.

491

Уравнивание целесообразно начинать с полигона, имеющего большую невязку. В этом случае количество приближений сокращается. В примере уравнивание следует начинать с полигона (1).

Полигон (1). Невязка + 15 мм.

Полигон (2). В этот полигон входит поправка хода (3), равная +3,2 мм. Поэтому перед распределением поправкок значение невязки полигона (2) следует исправить: +8,0 +3,2 = +11,2 мм.

Полигон (4).

Невязка в полигоне исправляется на величины уже известных поправок:

+13,0 + 5,0 + 4,5 = + 22,5 мм.

v1 = + 22,5 ×0,51 = + 11,5мм ;v5 = + 22,5 ×0,49 = + 11,0мм .

4. Далее вся процедура уравнивания повторяется, начиная последовательность действияй с полигона (1).

Следует иметь в виду, что в последующем во всех полигонах невязка будет образована суммой поправок, находящихся в табличках внутри полигона.

Полигон (1). Невязка: - 1,8 + 3,0 + 0,2 = +1,4 мм.

v1 = + 0,5 мм ; v1 = + 0,5 мм ; v1 = + 0,5 мм ; v1 = + 0,5 мм.

Полигон (2). Невязка: +0,3 – 1,7 + 0,3 = - 1,1 мм.

v3 = - 0,3 мм ; v5 = - 0,4 мм ; v6 = - 0,4 мм .

Полигон (3). Невязка: + 0,3 – 0,4 = - 0,1мм.

v4 = 0,0 мм (округлена) ; v6 = 0,0 мм (округлена) ; v7 = - 0,1 мм .

Полигон (4). Невязка: + 0,5 – 0,4 = + 0,1 мм. v5 = 0,0 мм ; v1 = + 0,1мм .

5.Под двойной чертой во всех табличках поправок получить их алгебраическую сумму.

6.Вычислить значения поправок по ходам.

Правило вычисления поправок следующее.

Для хода, принадлежащего двум смежным полигонам, поправка равна алгебраической сумме чисел внутренней и внешней табличек. При этом сумма поправок внешней таблички берется с обратным знаком:

-ход (1), полигон (1): - 1,7 + (-5,5) = - 7,2 мм;

-ход (1), полгон (4): + 5,5 + 1,7 = + 7,2 мм;

-ход (5), полигон (2): - 1,7 – 4,1 = - 5,8 мм;

-ход (5), полигон (4): + 4,1 + 1,7 = + 5,8 мм;

-ход (6), полигон (2): - 3,3 + 0,0 = - 3,3 мм;

-ход (6), полигон (3): + 3,3 + 0,0 = + 3,3 мм;

-ход (4), полигон (1): + 0,2 + (-3,6) = - 3,4 мм;

-ход (4), полигон (4): + 3,6 + (-0,2) = +3,4 мм.

492

Для свободного хода поправка соответствует вычисленной под двойной чертой таблички: ход (2): - 3,9 мм; ход (7): - 0,3 мм.

В данном случае окончательные значения поправок можно округлить до 1 мм. В особо ответственных случаях, например, в нивелирных сетях при измерениях деформаций сооружений, часто поправки округляют до 0,1 мм.

7. Вычислить уравненные превышения и высоты узловых точек (табл.

16.65).

Если направление хода при вычислении высот совпадает с направлением хода по полигону, которому принадлежит этот ход, то поправка в измеренное превышение вводится с тем же знаком, с которым она получена из уравнивания. Если не совпадает, то знак поправки берется обратным.

Как следует из таблицы 16.65 , значения уравненных высот отличаются не более, чем на 1 мм, что связано с округлением поправок.

§ 159. Способ последовательных приближений

Для иилюстрации способа последовательных приближений рассмотрим схему нивелирных ходов примера § 157 (способ эквивалентной замены).

1.В ведомость уравнивания (табл. 16.66 , столбцы 1-6) выписать исходные данные со схемы нивелирной сети (рис. 16.17) для каждой узловой точки (А, В, С), а также из табл. 16.64 – значения весов превышений.

2.1-е приближение. Точка А.

Вычислить высоту узловой точки В по результатам измерений. По формуле (3.39) получить среднее весовое значение высоты точки А по ходам (1)

и (5): НА(1) = 80,5054 м.

493

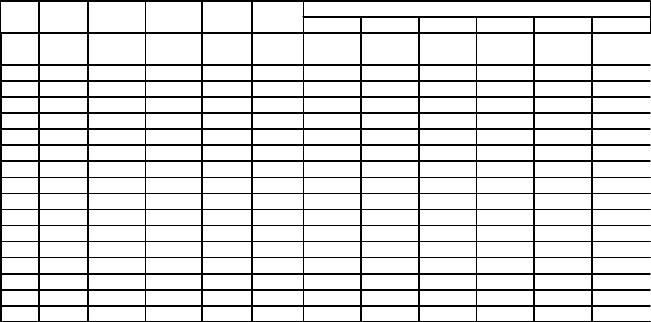
Таблица 16.66

1-е приближение. Точка В.

Вычислить среднее весовое значение высоты точки В по ходам (6) и (3), используя в ходе (3) среднее весовое значение высоты точки А:НВ(1)=81,7111 м.

1-е приближение. Точка С.

Вычислить среднее весовое значение высоты точки С по ходам (2) и (7), а также по ходу (4), используя среднее весовое значение точки В: НС(1) =

=80,0546 м.

3.Во втором приближении используются средние весовые значения высот точек А, В и С, полученные в 1-м приближении. В третьем приближении

–средние весовые значения высот, полученные во втором приближении и т.д. Высоты исходных реперов остаются одинаковыми во всех приближениях.

Второе, третье и последующие приближения выполняются по схеме, приведенной в п.2. Вычисления (приближения) прекращаются до повторения высот точек в двух соседних шагах, т.е. при первом повторении результатов средних весовых значений высот узловых точек.

4.Вычислить поправки в измеренные превышения по формуле

где H0 – уравненное значение высоты узловой точки; Hi – значение высоты узловой точки по i-му ходу.

Получим значения поправок в превышения по последнему приближению:

494